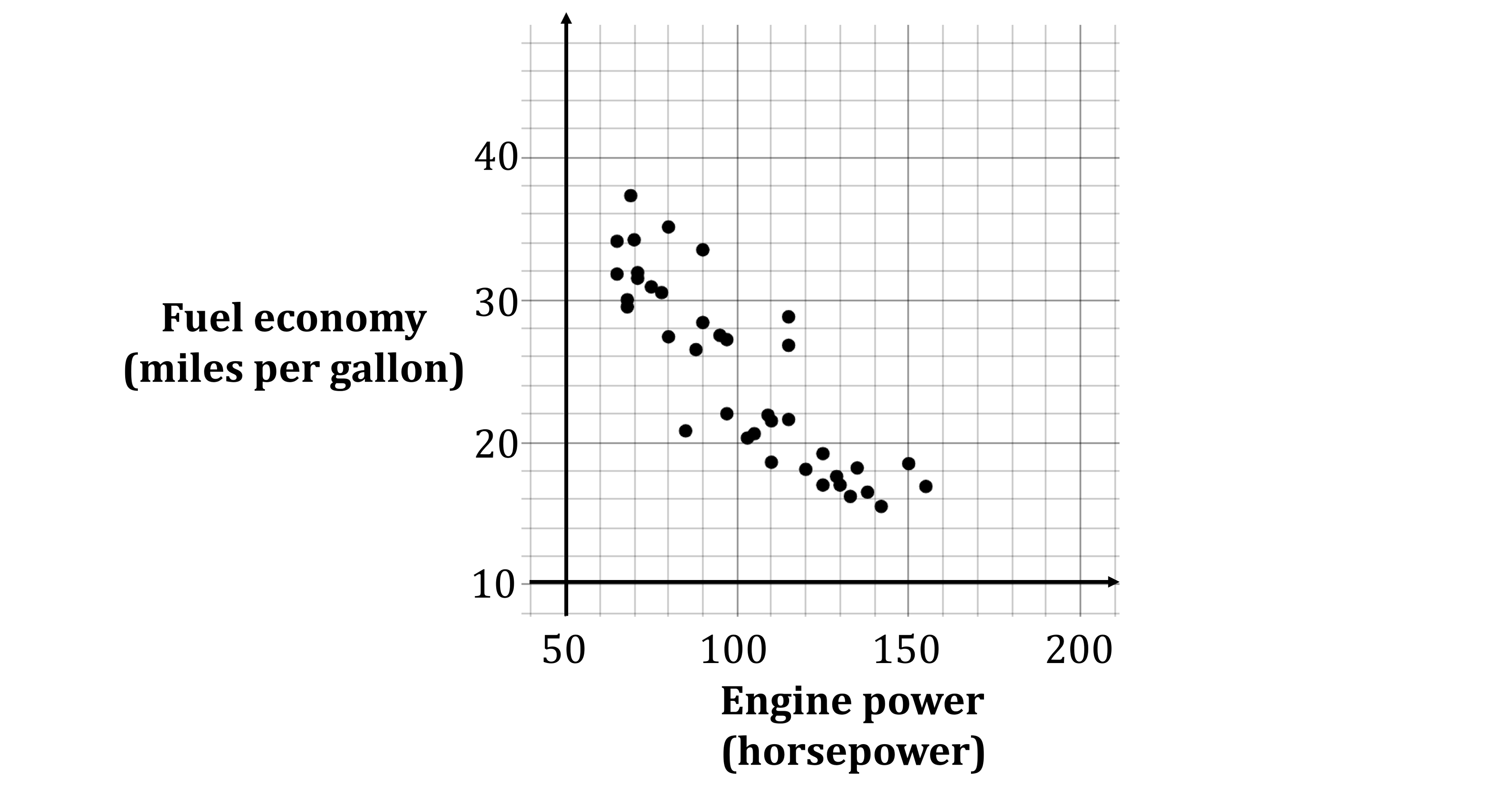
Andrea collects data on the power (in horsepower) and the fuel economy during city driving (in miles per gallon) for each car in a sample of 38 cars of various types. The scatter diagram was drawn for this information by statistical software.
Source: www.dasl.datadescription.com
Describe and interpret the type of correlation shown by the scatter diagram.
The mean of the engine powers in the sample is 101.7 horsepower, to 1 decimal place.
The sum of the fuel economies in the sample is 940.9.
On the scatter diagram,
(i) Find the double mean point of the data,
[2]
(ii) draw a line of best fit through the double mean point.
[1]
Andrea wants to predict the fuel economy of a car with 190 horsepower.
Explain why it is not appropriate to use the line of best fit on this scatter diagram to find this prediction.
Did this page help you?







