Revision NotesExam QuestionsPast Papers
GCSEStatisticsEdexcelHigherRevision NotesProcessing, Representing & Analysing DataTime SeriesIdentifying & Interpreting Trends in Data

Identifying & Interpreting Trends in Data (Edexcel GCSE Statistics)

Revision Note

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Edexcel Statistics: HigherEdexcel Statistics: Foundation

Trend Lines

How do I draw trend lines on a time series graph?

  • Time series graphs can go up and down over time

    • This can make it hard to see what the general trend of the data is

      • e.g. are things 'on average' tending to increase, decrease, or stay the same over time

  • A trend line is a line drawn on a time series graph to help identify the general trend

  • It is possible to draw a trend line by eye directly from a time series graph

    • In this case the line should go approximately halfway between the lowest and highest points for each cycle (most often the cycle will be a year)

  • Usually however the trend line will be drawn by eye using moving average points plotted on the time series graph

    • In this case the trend line is a line of best fit for those moving average points

      • This is more accurate than simply drawing the line from the raw data points on the time series graph

      • This should be a single straight line going approximately through the moving average points

        • It does not mean connecting the moving average points point to point!

Examiner Tips and Tricks

  • Remember to use a ruler when drawing a trend line

Worked Example

The time series graph shows the number of visitors to Wayne’s World of Widgets for 2021, 2022 and the first two quarters of 2023.

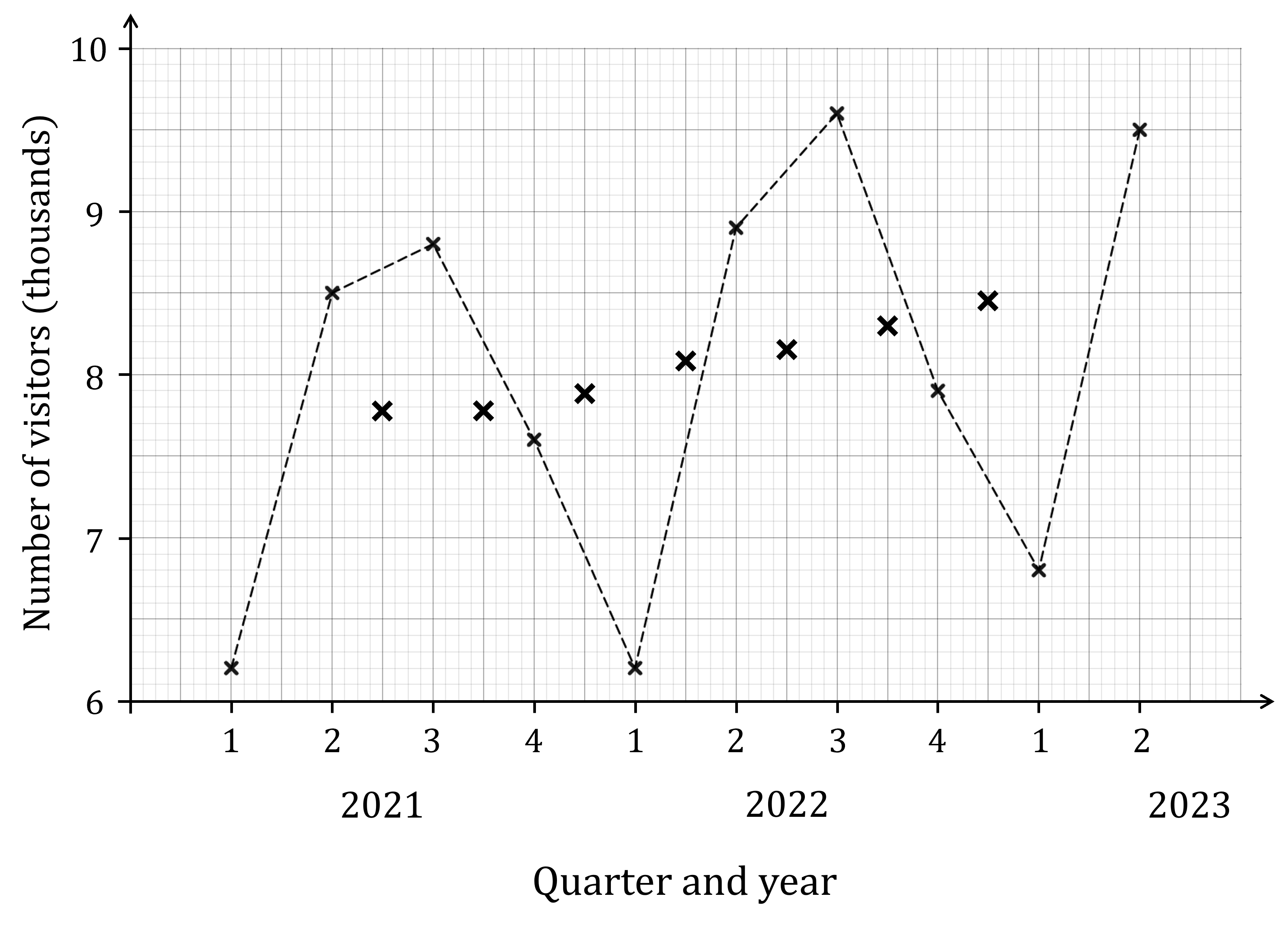
A time series graph with moving averages added

The moving average points for the four point moving averages have also been plotted on the graph.

Draw a trend line on the graph for this data.

The trend line needs to be a straight line that is the line all the moving average points approximately lie along

Remember, it is not drawn by connecting the moving average points point to point!

The time series graph from the question with the trend line drawn on

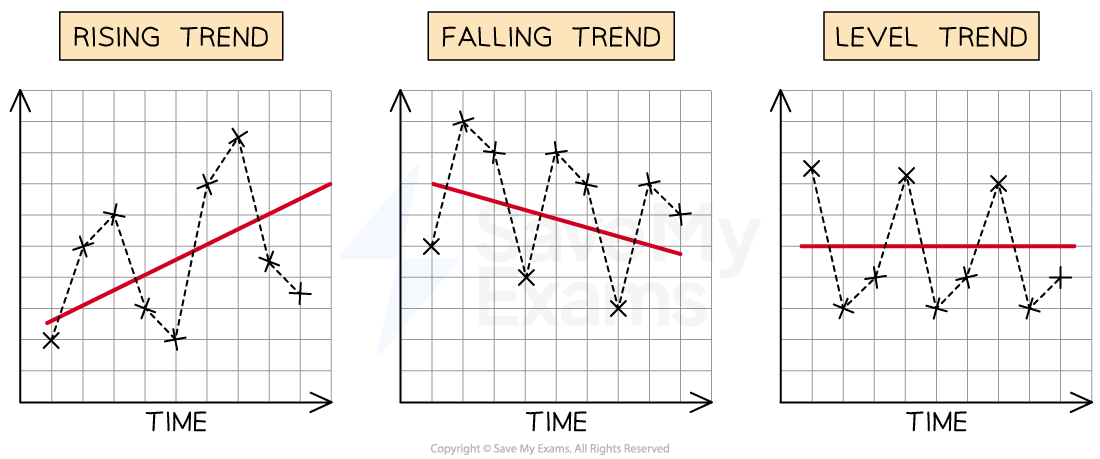
  • There are two types of trend that you should be able to identify and interpret on a time series graph

  • The general trend is the 'average behaviour' of the data over time

    • The general trend can be seen from the trend line for the data

      • If the trend line goes up over time (i.e. has a positive gradient) then we say there is a rising trend

      • If the trend line goes down over time (i.e. has a negative gradient) then we say there is a falling trend

      • If the trend line stays the same over time (i.e. is horizontal) then we say there is a level trend

Examples of rising, falling and level trends on time series graphs

  • Seasonal or cyclical trends are patterns in the data that repeat over time

    • For example an ice cream shop may see higher sales every summer and lower sales every winter

    • Or a town centre restaurant may see higher customer numbers on weekend evenings and lower customer numbers on weekday evenings

    • These sorts of trends appear as repeating patterns on a time series graph

Examiner Tips and Tricks

  • When commenting on trends on an exam question be sure to comment in the context of the question

    • For example don't just say 'There is a rising trend'

    • But be sure to add something like 'This shows that sales are increasing over time'

Worked Example

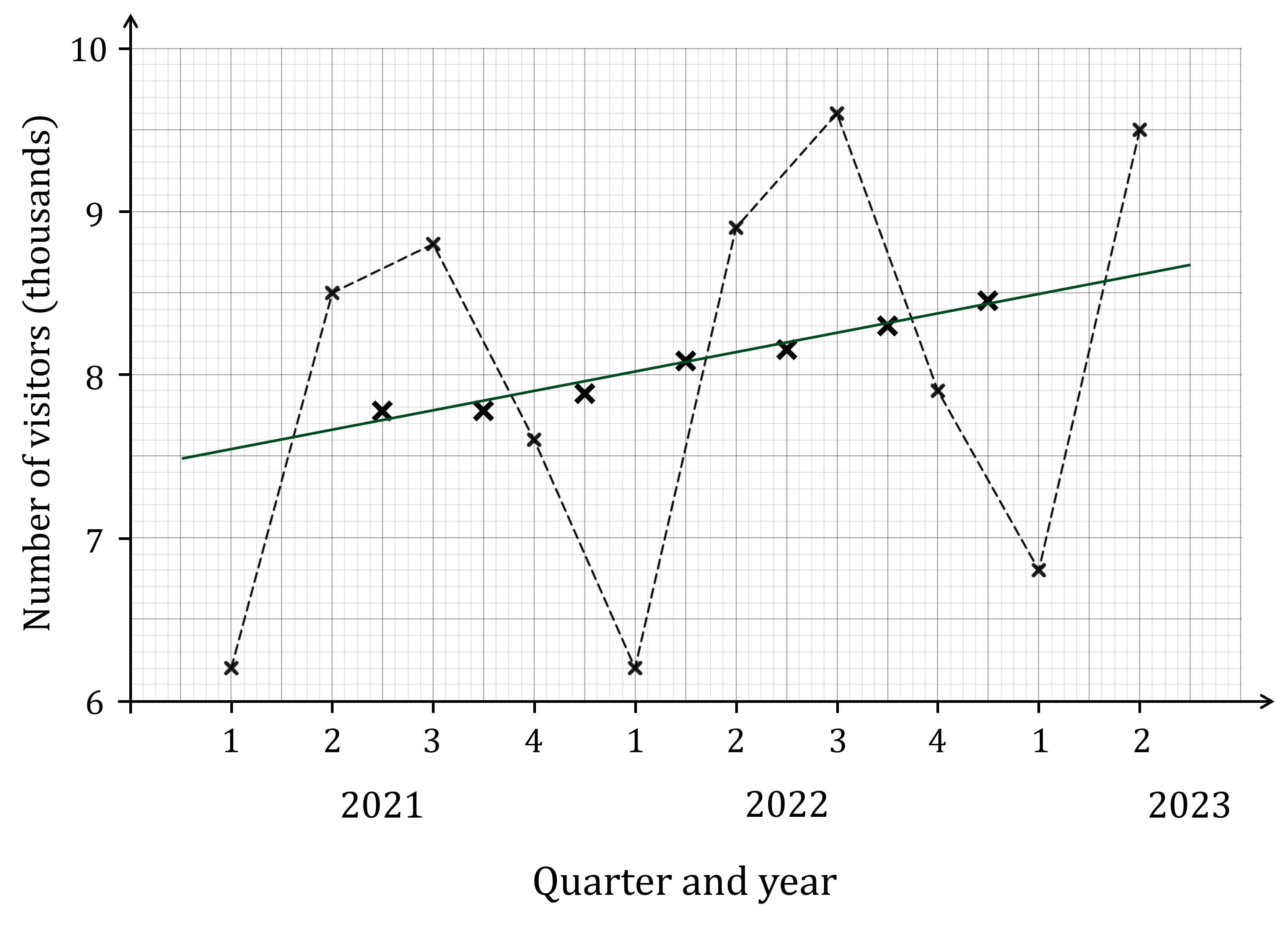
The time series graph shows the number of visitors to Wayne’s World of Widgets for 2021, 2022 and the first two quarters of 2023.

A time series graph with moving average points and a trend line drawn on

The moving average points for the four point moving averages have also been plotted on the graph, along with the trend line based on those points.

(a) Describe the general trend shown in the data.

The trend line is going up (has a positive gradient), so there is a rising trend
This means visitor numbers are increasing over time

The trend line is going up from left to right, which means there is a rising trend. The number of visitors to Wayne's World of Widgets is tending to increase over time.

(b) Describe the seasonal variations shown in the data, and suggest a reason for why these variations occur.

Note that the visitor numbers each year are higher than the trend line in quarters 2 (April to June) and 3 (July to September), and lower than the trend line in quarters 1 (January to March) and 4 (October to December)

This suggests that more people are visiting in the spring and summer months (while people are on holiday and the weather is nice), and less are visiting in the autumn and winter months (when people are travelling less and the weather isn't as nice)

The numbers of visitors are above the trend line for quarters 2 and 3 each year, and lower than the trend line for quarters 1 and 4 each year. More people are visiting Wayne's World of Widgets in the spring and summer months when the weather is nice and people tend to be on holiday, and less people are visiting in the autumn and winter.

Mean Seasonal Variation

What is mean seasonal variation?

  • The mean seasonal variation describes the average way that a seasonal value is different from the value on a trend line

    • It is also called the average seasonal effect

    • Make sure you are familiar with both terms!

  • First you need to calculate the seasonal variation for points on the graph

    • seasonal space variation space at space straight a space point space equals space actual space value space minus space trend space line space value

    • You will do this for all the ‘same seasons’ in the data set

      • For example, for all the ‘Quarter 1’ points for the different years on a time series graph

    • These values can be positive or negative

  • The mean seasonal variation for a season is the mean of the seasonal variations for that season

    • Add them together and divide by how many there are

      • Don’t forget the minus signs if the seasonal variations are negative

How can I use the mean seasonal variation to make predictions?

  • To make predictions, the trend line needs to be extended to the right

    • i.e. beyond the last known values in the data set

  • Then

    • predicted space value space equals space trend space line space value space plus space mean space seasonal space variation

  • Be aware that in going beyond the known data you are extrapolating, which is not always reliable

    • The prediction becomes less reliable the further into the future it is made for

    • It is most reliable when predicting only one cycle beyond the last known value

    • Trends and seasonal variations can also change unexpectedly

Examiner Tips and Tricks

  • An exam question may refer to either ‘mean seasonal variation’ or ‘average seasonal effect’

    • They both mean the same thing

  • For seasonal variations make sure to subtract the right way round

    • If the actual value is below the trend line the seasonal variation will be negative

Worked Example

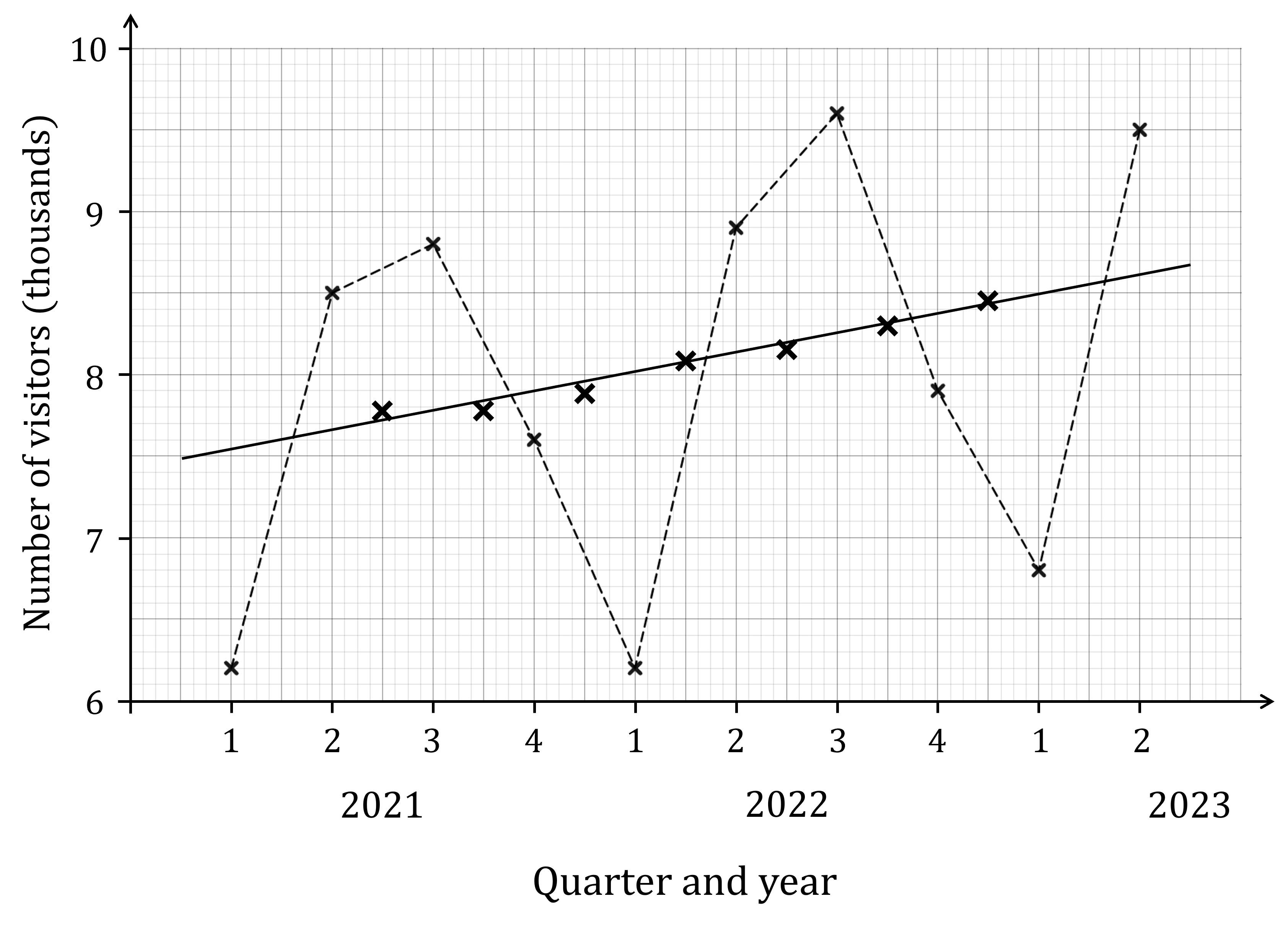
The time series graph shows some information about the number of visitors to Wayne’s World of Widgets from 2021 to 2023.  The trend line based on the moving point averages has also been drawn on the graph.

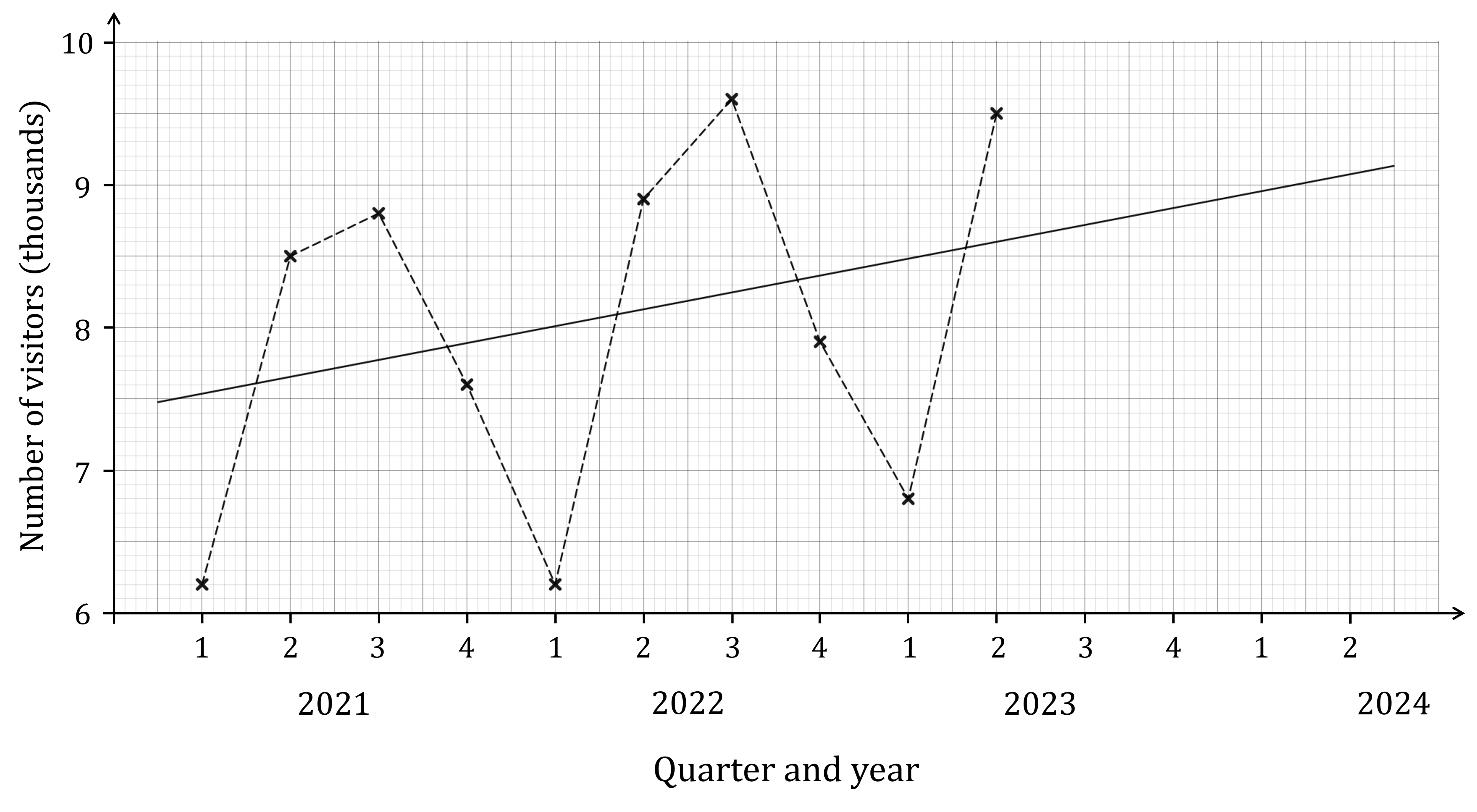
Time series graph with trend line

(a)  Calculate the average seasonal effects for Quarters 1 and  2.

We need to read the Quarter 1 and Quarter 2 values off the trend line for 2021, 2022 and 2023

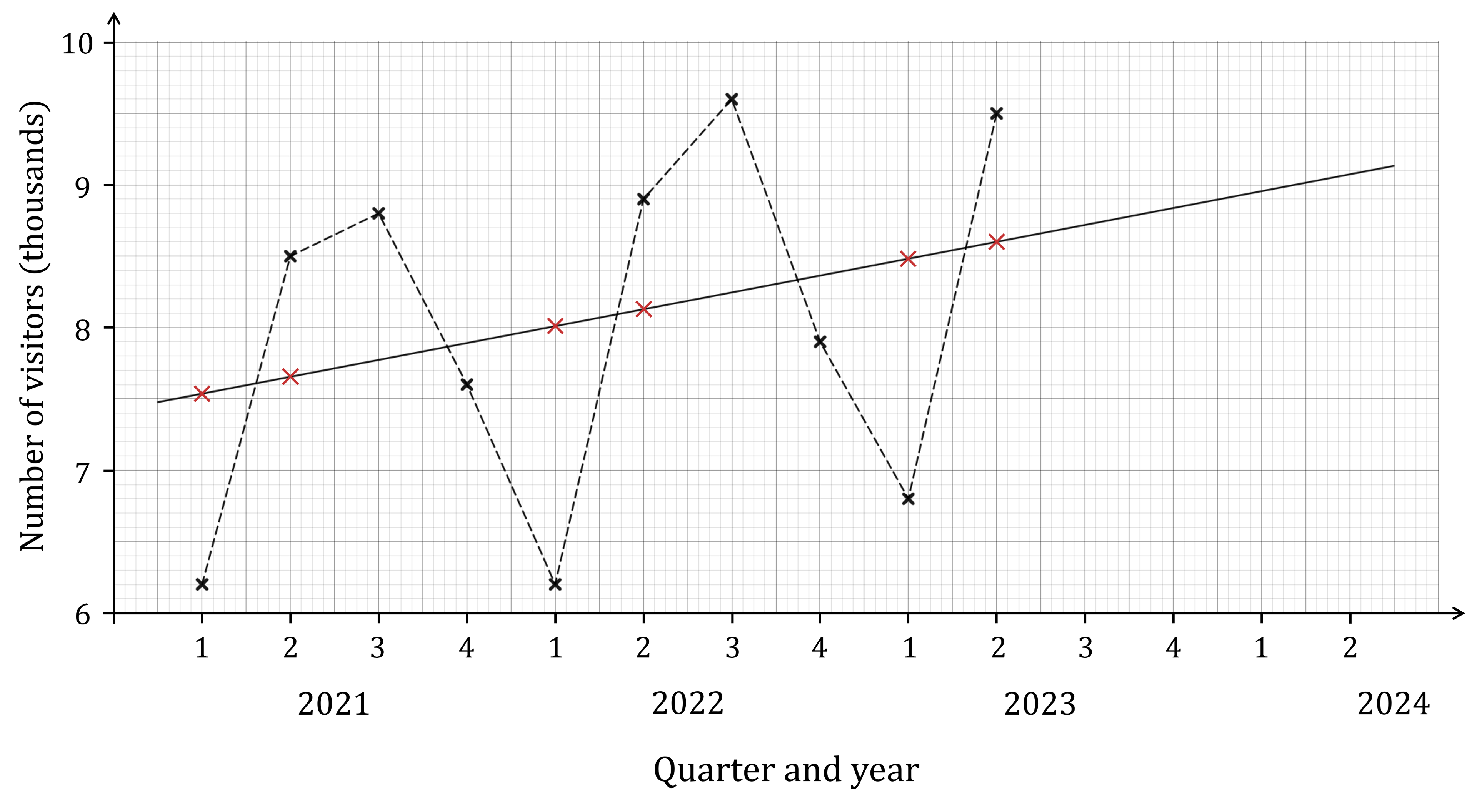
Time series graph and trend line with Quarter 1 and Quarter 2 points marked on the trend line

First find the seasonal variations for Quarter 1

Remember it's actual value minus trend line value

Quarter 1

2021 colon space space 6.2 minus 7.54 equals negative 1.34

2022 colon space space 6.2 minus 8.01 equals negative 1.81

2023 colon space space 6.8 minus 8.48 equals negative 1.68

The average seasonal effect for Quarter 1 is the mean of those three values

fraction numerator negative 1.34 plus open parentheses negative 1.81 close parentheses plus open parentheses negative 1.68 close parentheses over denominator 3 end fraction equals negative 1.61

The average seasonal effect for Quarter 1 is -1.61 thousand visitors

A range of answers would be accepted to allow for variations in reading off graphs

Writing -1610 visitors would also be accepted

Now do the same thing for Quarter 2

Quarter 2

2021 colon space space 8.5 minus 7.66 equals 0.84

2022 colon space space 8.9 minus 8.12 equals 0.78

2023 colon space space 9.5 minus 8.6 equals 0.9

fraction numerator 0.84 plus 0.78 plus 0.9 over denominator 3 end fraction equals 0.84

The average seasonal effect for Quarter 2 is 0.84 thousand visitors

A range of answers would be accepted to allow for variations in reading off graphs

Writing 840 visitors would also be accepted

(b)  Hence predict the numbers of visitors for Quarters 1 and 2 of 2024.

We need to read the Quarter 1 and Quarter 2 values off the trend line for 2024

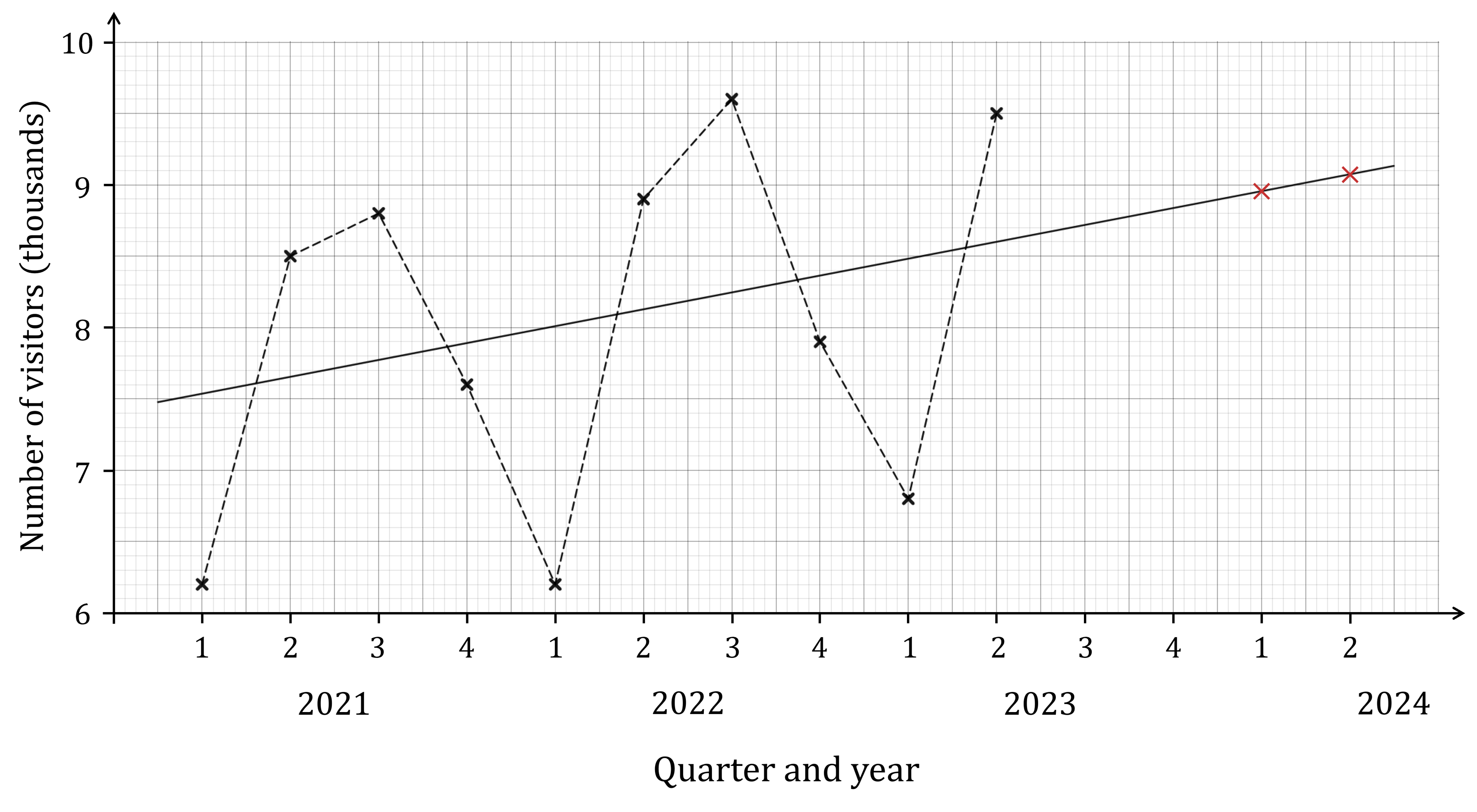
Time series graph and trend line with future Quarter 1 and Quarter 2 points on the trend line marked

The predicted value for a quarter is the value from the trend line plus the average seasonal effect

If the average seasonal effect is negative, this will give a prediction lower than the trend line value

Quarter 1:  8.95 plus left parenthesis negative 1.61 right parenthesis equals 7.34

Quarter 2:  9.07 plus 0.84 equals 9.91

Remember that those numbers are thousands of visitors!

7.34 cross times 1000 equals 7340

9.91 cross times 1000 equals 9910

The predicted number of visitors for Quarter 1 in 2024 is 7340 visitors

The predicted number of visitors for Quarter 2 in 2024 is 9910 visitors

A range of answers would be accepted to allow for variations in reading off graphs

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Moving AveragesNext:Quality Assurance
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.