Pie Charts (Edexcel GCSE Statistics)

Revision Note

Written by: Roger B

Reviewed by: Dan Finlay

Pie Charts

What is a pie chart?

A pie chart is a circle which is divided into slices (sectors) to show proportions
They show the relative size of categories of data compared to each other
- rather than their actual size or number
  - e.g. looking at the proportions of men and women working for a company, we might be more interested in the relative sizes of the groups than in the actual numbers of men and women
There are 360° in a circle
- We can use this to help us calculate the size of each slice of the pie chart

How do I draw a pie chart?

This is shown easiest through an example
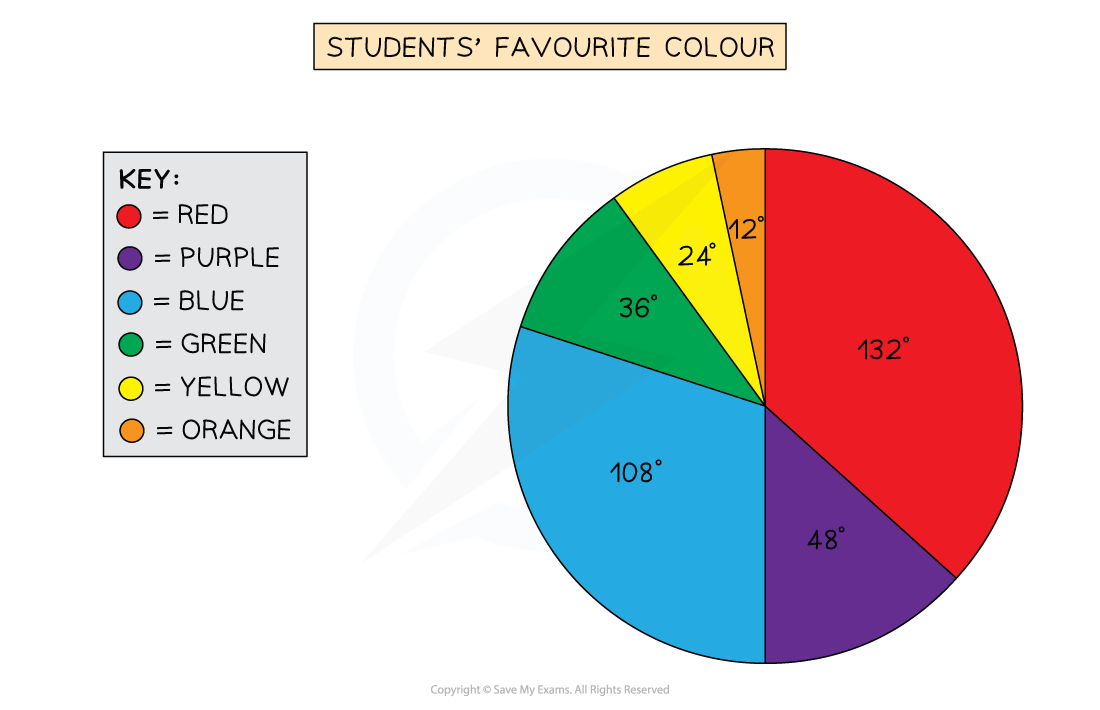
The following data is collected for a class of 30 students about their favourite colour

Colour	Red	Purple	Blue	Green	Yellow	Orange
Students	11	4	9	3	2	1

STEP 1
Find the number of degrees that represents 1 student
- There are 30 students in total, so 360° = 30 students
- Divide both sides by 30, so 12° = 1 student
STEP 2
Calculate the angle for each category by finding a fraction of 360°
- 11 students out of 30 said red was their favourite colour,
  - so this is $\frac{11}{30} \times 360 ° = 132 °$
- 4 students out of 30 said purple,
  - so this is $\frac{4}{30} \times 360 ° = 48 °$
- Repeat this for each category, they should sum to 360° in total

Colour	Red	Purple	Blue	Green	Yellow	Orange
Students	11	4	9	3	2	1
Angle	132°	48°	108°	36°	24°	12°

STEP 3
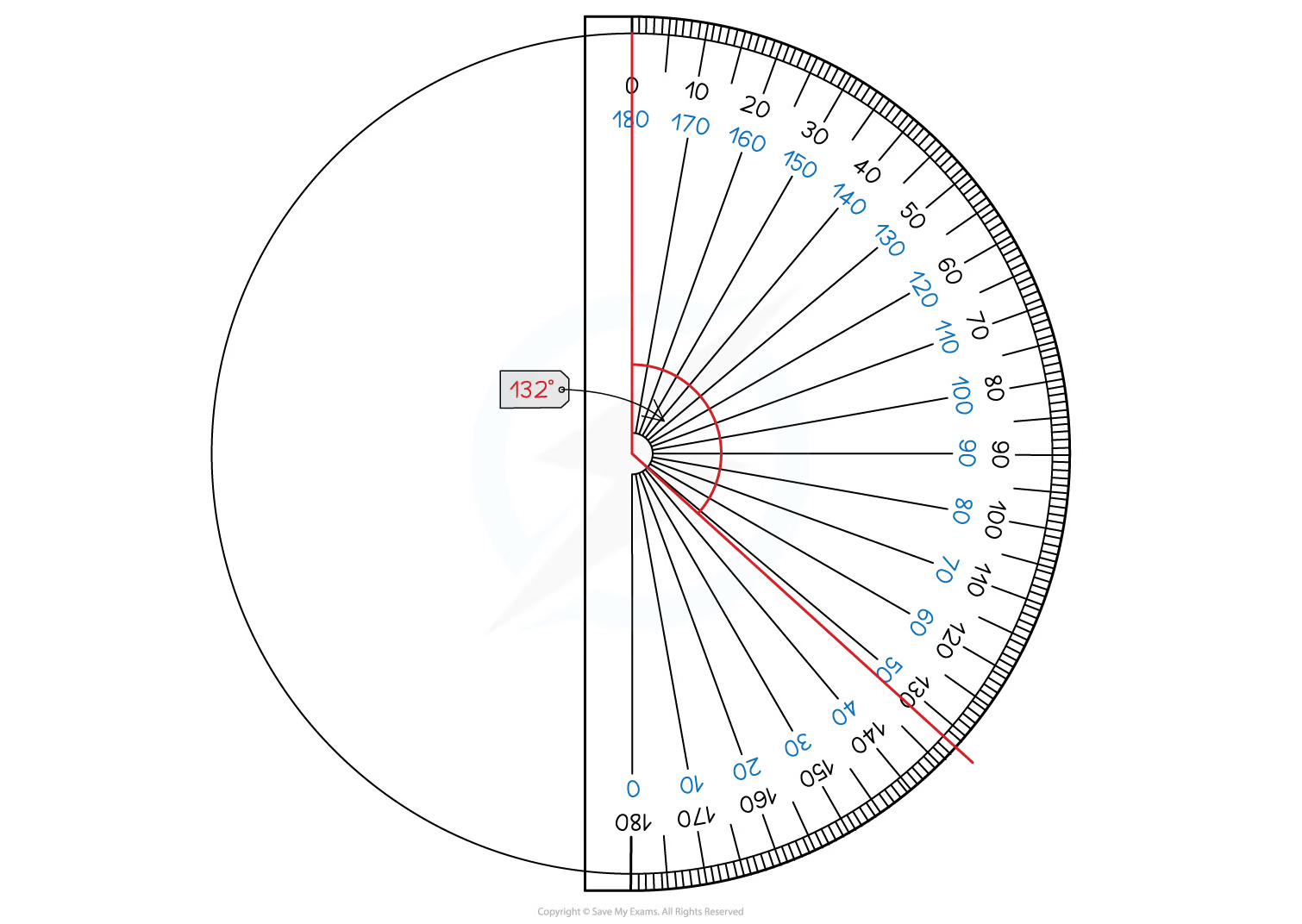
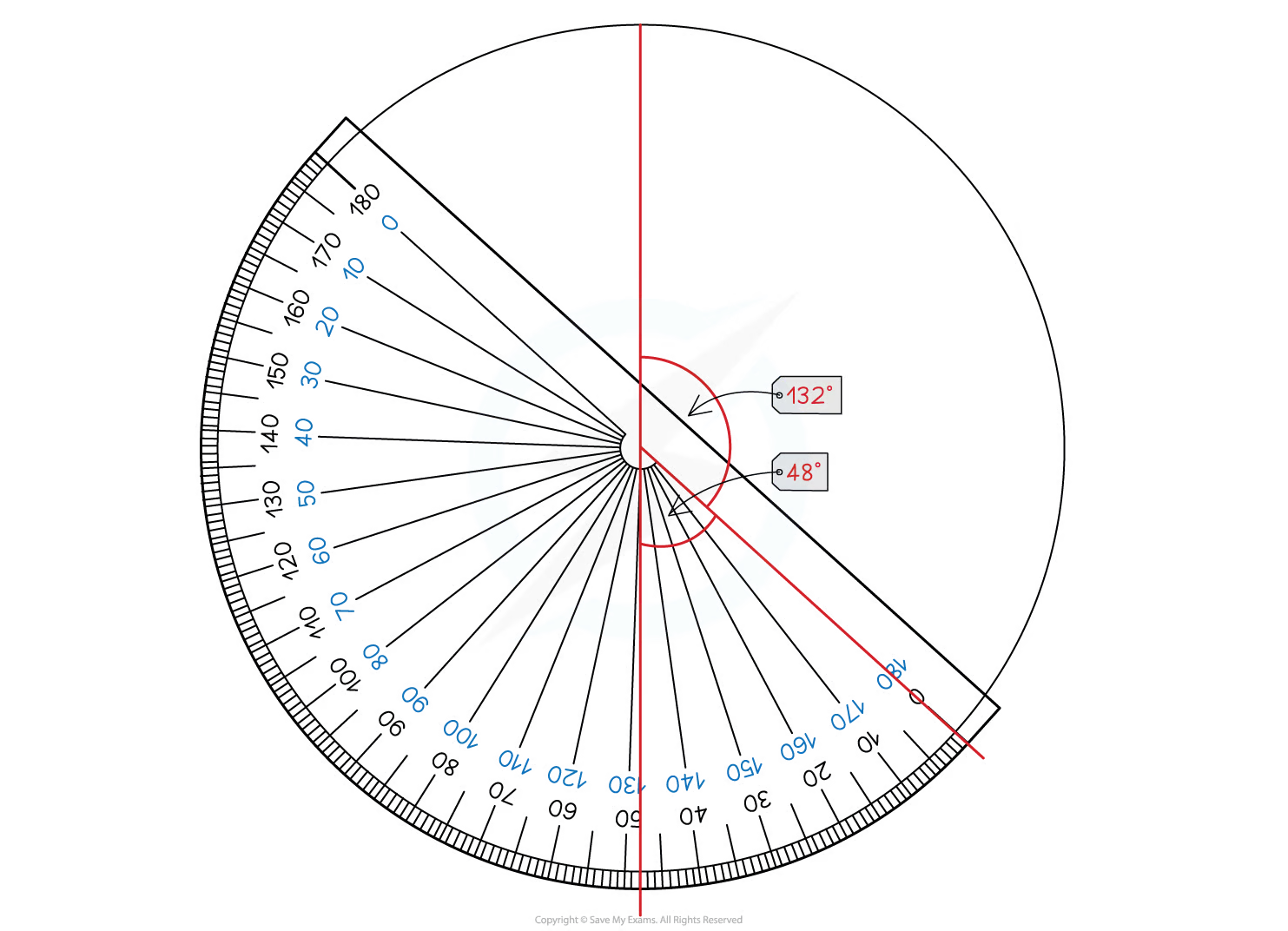
Draw the pie chart, using a protractor to measure the angles
- Start by drawing a vertical line from the centre of the circle to the top ("12 o'clock")
- Then use your protractor to measure the first angle and draw a line to this point
- Move your protractor to this line, and repeat for the next category
- Continue until the slices for all the categories are drawn
- You should include a key or labels to show which slice represents which category

How do I interpret a pie chart or find missing information?

It is easy to spot from a pie chart which category is the largest or smallest proportion
- But you may be asked to do something more advanced like finding some missing information
- Remember that all of the data is represented by 360°
You can use the information you are given to find
- how many degrees each person/piece of data is represented by
- how many people/pieces of data 1 degree represents
For example if you are told that there is a slice measuring 30° which represents 15 people
- 30° = 15 people
  - 1° = 0.5 people (divide by 30)
  - 2° = 1 person (divide the first statement by 15, or double the second statement)
- You can then use this information to help solve problems or find missing information

Examiner Tips and Tricks

A pie chart given in an exam may not be to scale
- If it is not to scale, do not try to use your protractor to measure it!
- Instead use the methods described in this revision note to calculate the information you need

Worked Example

The following pie chart is created to show the total value of items stocked in a sports shop for 4 different sports.

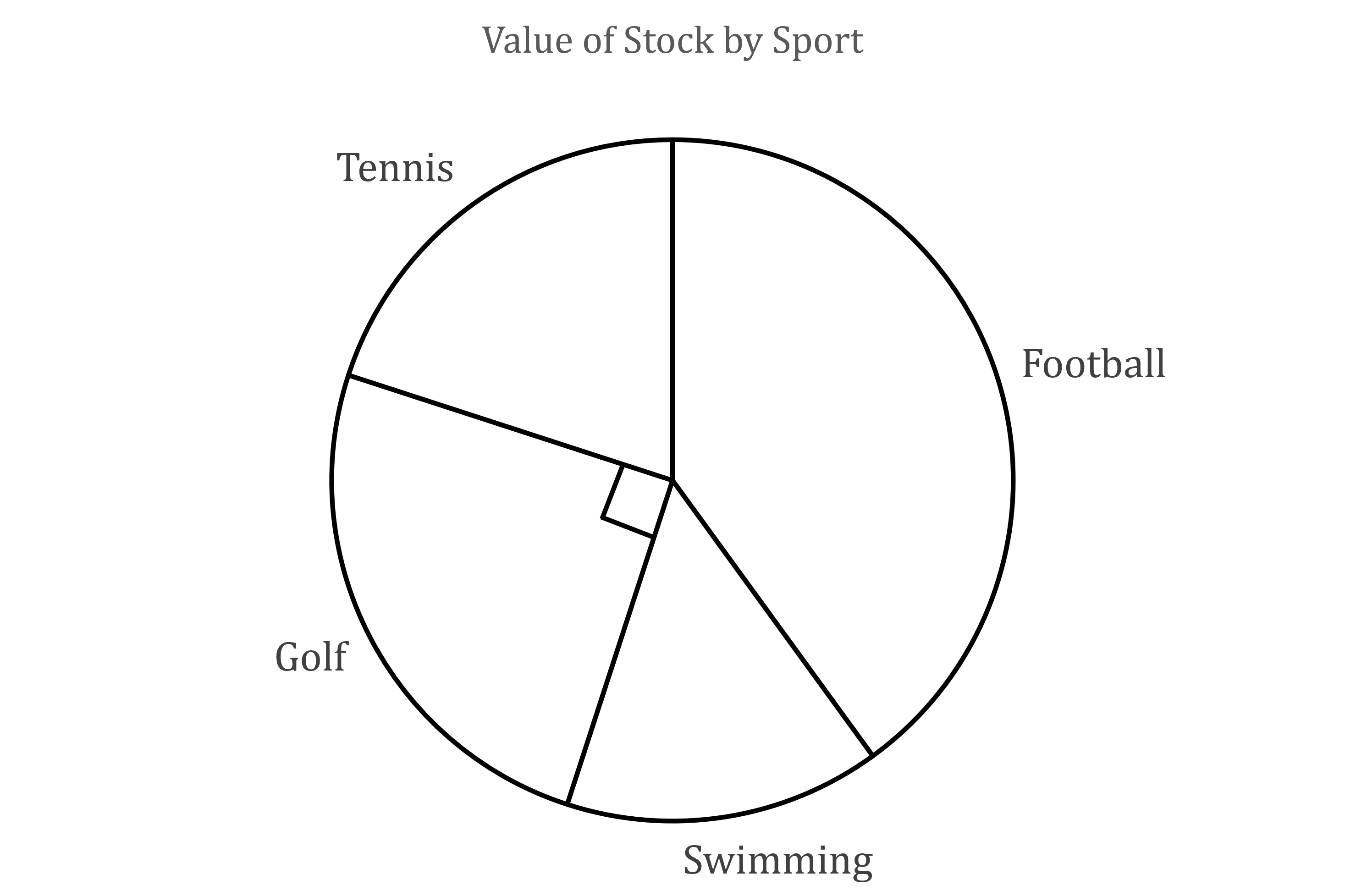
(a) Using the angle marked on the pie chart, and the fact that the shop stocks $12 000 worth of Golf items, find the total value of the shop’s stock across the 4 sports.

The angle marked on the diagram is 90°

$\frac{90}{360} = \frac{1}{4}$

So a quarter of the stock is for golf
That means we can multiply the value of the golf stock by 4 to find the total value of the shop’s stock

$12000 \times 4 = 48000$

Total value is $48 000

(b) Given that the angle on the pie chart for Tennis is 72°, find the value of the Tennis items that the shop stocks.

The fraction of the value of the shop’s stock will be the same as the fraction of the circle for each category

Therefore the value of tennis items will be

$48000 \times \frac{72}{360} = 9600$

Value of tennis items is $9 600

Comparative Pie Charts

How are comparative pie charts different from regular pie charts?

For two data sets of different sizes (different total frequencies), drawing two pie charts that are the same size can be misleading
- It makes it 'look like' the two sets are the same size
- A sector ('slice') in one pie chart can be the same size as a sector in the other one
  - even though the number of things represented can be very different
With comparative pie charts, the areas of the two pie charts are in the same ratio as the total frequencies of the two data sets
- e.g. if one pie chart represents data for 500 people and the other one represents data for 1000 people
- then the area of the second chart will be twice as big as the area of the first one
  - because $500 : 1000 = 1 : 2$
The relationship between the radiuses of two pie charts and the total frequencies of their data sets can be given by the formula
- $\frac{F_{2}}{F_{1}} = \frac{{r_{2}}^{2}}{{r_{1}}^{2}}$
  - $r_{1}$ is the radius of the pie chart for data set 1
  - $F_{1}$ is the total frequency of data set 1
  - $r_{2}$ is the radius of the pie chart for data set 2
  - $F_{2}$ is the total frequency of data set 2
- It can be rearranged as $r_{2} = r_{1} \times \sqrt{\frac{F_{2}}{F_{1}}}$
  - This can be used to find $r_{2}$ if you know the other three values
- Or as $F_{2} = F_{1} \times \frac{{r_{2}}^{2}}{{r_{1}}^{2}}$
  - This can be used to find $F_{2}$ if you know the other three values
The formula is not in the formula booklet so you need to remember it
- It might help if you understand where it comes from
  - Remember that the area of a circle is $π r^{2}$
  - So we want the areas to give $F_{2} : F_{1} = π {r_{2}}^{2} : π {r_{1}}^{2}$
  - That's the same as $\frac{F_{2}}{F_{1}} = \frac{π {r_{2}}^{2}}{π {r_{1}}^{2}}$
  - Cancel the $π$ 's to get $\frac{F_{2}}{F_{1}} = \frac{{r_{2}}^{2}}{{r_{1}}^{2}}$
- To get the ' $r_{2} =$ ' version
  - multiply both sides by ${r_{1}}^{2}$ to get ${r_{2}}^{2} = {r_{1}}^{2} \times \frac{F_{2}}{F_{1}}$
  - then take square roots: $r_{2} = \sqrt{{r_{1}}^{2} \times \frac{F_{2}}{F_{1}}} = r_{1} \times \sqrt{\frac{F_{2}}{F_{1}}}$
- To get the ' $F_{2} =$ ' version
  - multiply both sides by $F_{1}$ to get $F_{2} = F_{1} \times \frac{{r_{2}}^{2}}{{r_{1}}^{2}}$

How do I compare two data sets represented by comparative pie charts?

When comparing two data sets represented by comparative pie charts:
- To compare frequencies compare areas
  - This is true for the total frequencies
  - It is also true for the frequencies of individual sectors
- To compare proportions compare the angles of the sectors
If a question asks you about frequencies of individual sectors
- it is may be easier to find the total frequencies of the pie charts first
- See the Worked Example

Examiner Tips and Tricks

If the question tells you that comparative pie charts are "drawn accurately", then you can find
- their radiuses by measuring with your ruler
- the angles of sectors by measuring with your protractor

Worked Example

In 2022, a cruise line started offering combined '18-30, 45-55 and 70+' cruises.

The comparative pie charts show information about the numbers of people from each age group that went on these cruises in 2022 and in 2023.

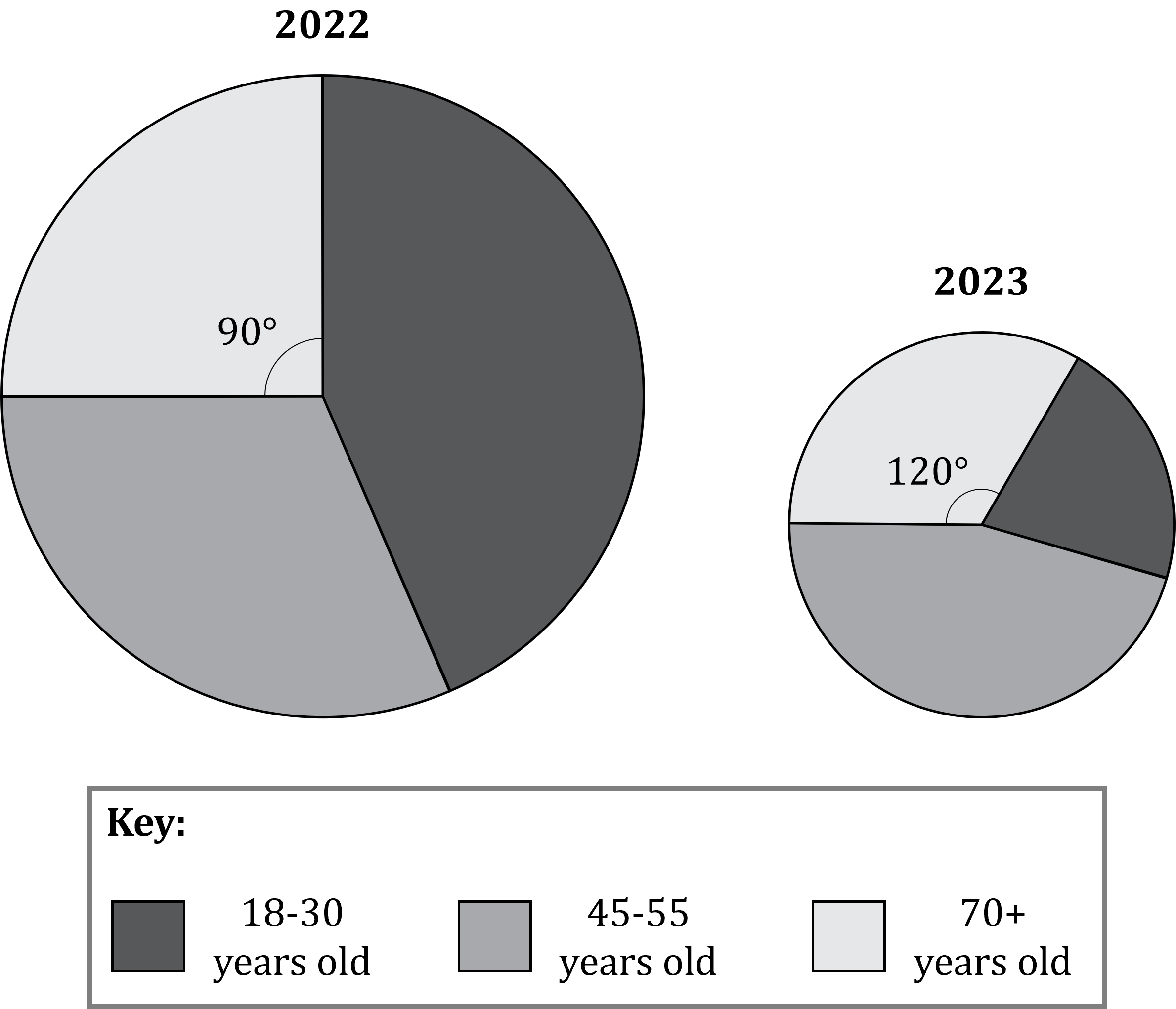
Comparative pie charts for the two data sets referred to in the question

The radius of the pie chart for 2023 is smaller than the radius of the pie chart for 2022.

(a) Explain what can be deduced from this information.

A smaller radius means a smaller area
And with comparative pie charts a smaller area means a smaller total frequency

Fewer people went on the cruises in 2023

1250 people who were 70+ years old went on the cruises in 2022.

The radius of the 2022 pie chart is 5 cm, and the radius of the 2023 pie chart is 3 cm.

(b) Work out the number of people who were 70+ years old that went on the cruises in 2023.

Work out the total number of people who went on cruises in 2022
$\frac{90}{360}$ of the 2022 circle is taken up by the '70+' sector
That corresponds to 1250 people, so

$\begin{array}{rcl} \frac{90}{360} \times 2022 total & = & 1250 \\ \frac{1}{4} \times 2022 total & = & 1250 \end{array}$

Divide both sides by $\frac{1}{4}$

$2022 total = 1250 \div \frac{1}{4} = 1250 \times 4 = 5000$

Use $\frac{F_{2}}{F_{1}} = \frac{{r_{2}}^{2}}{{r_{1}}^{2}}$ to find the total number of people for 2023
$F_{1} = 5000$ , $r_{1} = 5$ and $r_{2} = 3$
$F_{2}$ will then be the total frequency for 2023

$\frac{2023 total}{5000} = \frac{3^{2}}{5^{2}}$

Multiply both sides by 5000

$2023 total = 5000 \times \frac{3^{2}}{5^{2}} = 5000 \times \frac{9}{25} = 1800$

Now work out the number of people 70+ years old who went on cruises in 2023
$\frac{120}{360}$ of the 2023 circle is taken up by the '70+' sector, so

$\frac{120}{360} \times 1800 = \frac{1}{3} \times 1800 = 600$

600 people who were 70+ years old went on the cruises in 2023

Last updated: 7 May 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Next topic

Did this page help you?

Pie Charts (Edexcel GCSE Statistics)

Revision Note

Pie Charts

What is a pie chart?

How do I draw a pie chart?

How do I interpret a pie chart or find missing information?

Examiner Tips and Tricks

Worked Example

Comparative Pie Charts

How are comparative pie charts different from regular pie charts?

How do I compare two data sets represented by comparative pie charts?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay