Histograms & Frequency Polygons (Edexcel GCSE Statistics): Revision Note
Exam code: 1ST0
Frequency Polygons
What is a frequency polygon?
Frequency polygons are a very simple way of showing frequencies for continuous, grouped data
They give a quick guide to how frequencies change from one class interval to the next
What are the key features of a frequency polygon?
Apart from plotting and joining up points with straight lines there are 3 rules for frequency polygons:
Plot points at the midpoint of class intervals
Unless one of the frequencies is 0 do not join the frequency polygon to the x-axis
Do not join the first point to the last one
The result is not actually a polygon
It's more of an 'open' polygon that ‘floats’ in mid-air!
You may be asked to draw a frequency polygon and/or use it to make comments and compare data
How do I draw a frequency polygon?
This is most easily shown by an example
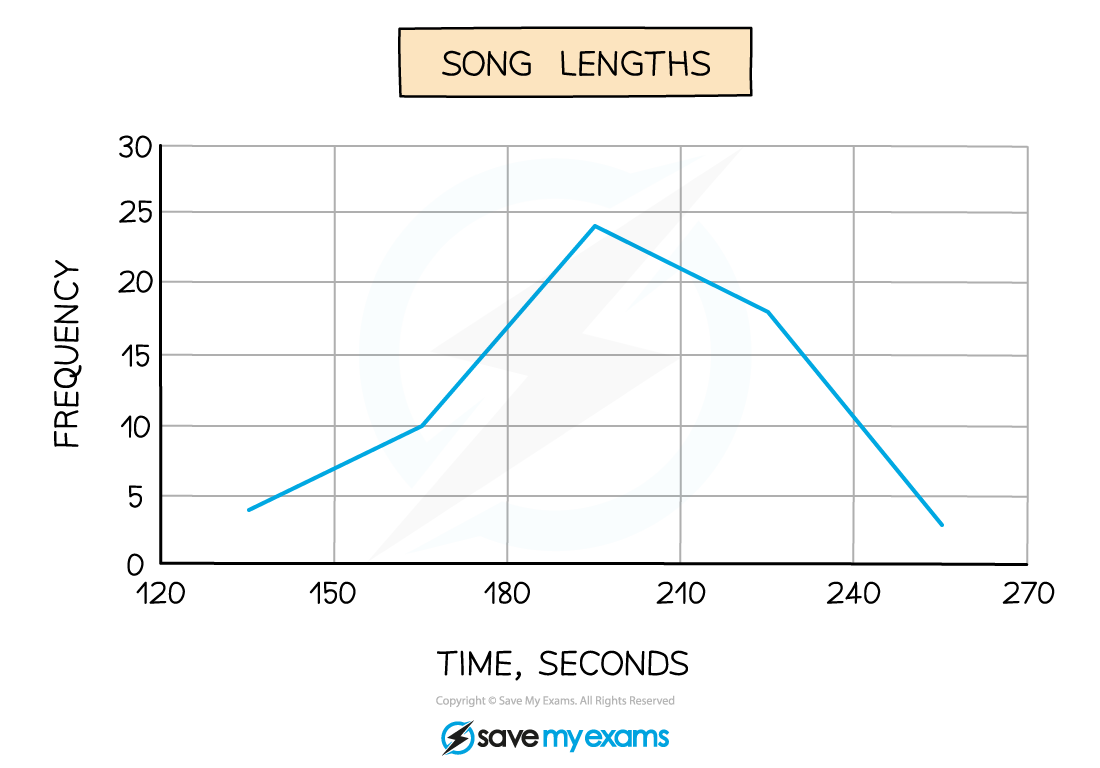
e.g. The lengths of 59 songs, in seconds, are recorded in the table below
Song length | Frequency |
120 ≤ t < 150 | 4 |
150 ≤ t < 180 | 10 |
180 ≤ t < 210 | 24 |
210 ≤ t < 240 | 18 |
240 ≤ t < 270 | 3 |
Frequencies are plotted at the midpoints of the class intervals, so in this case we would plot the points (135, 4), (165, 10), (195, 24), (225, 18) and (255, 3).
Join these up with straight lines (but do not join the last to the first!)
If you have a histogram with equal class widths
then a frequency polygon can be drawn
by marking the points at the centres of the tops of all the histogram bars
and joining those points together to make the 'polygon'
How do I use and interpret a frequency polygon?
Think about what you could you say about the data above, particularly by looking at the diagram only
The two things to look for are averages and spread
The modal class is 180 ≤ t < 210
Because the graph reaches its highest point there
It would be acceptable to say that 195 seconds is (an estimate of) the modal song length
The diagram (rather than the table) shows (an estimate of) the range of song lengths is 255 – 135 = 120 seconds
i.e. midpoint of highest class interval minus midpoint of lowest class interval
If 2 frequency polygons are drawn on the same graph comparisons between the 2 sets of data can be made
Examiner Tips and Tricks
Jot down the midpoints next to the frequencies so you are not trying to work them out in your head while also concentrating on actually plotting the points
Worked Example
A local council ran a campaign to encourage households to waste less food.
To compare the impact of the campaign the council recorded the weight of food waste produced by 30 households in a week both before and after the campaign.
The results are shown in the table below.
Food waste | Frequency | Frequency |
1 ≤ w < 1.4 | 3 | 5 |
1.4 ≤ w < 1.8 | 4 | 8 |
1.8 ≤ w < 2.2 | 8 | 14 |
2.2 ≤ w < 2.6 | 10 | 3 |
2.6 ≤ w < 3 | 5 | 1 |
(a) On the same diagram, draw two frequency polygons, one for before the council’s campaign and one for after.
Remember to include a key to show which frequency polygon is which.
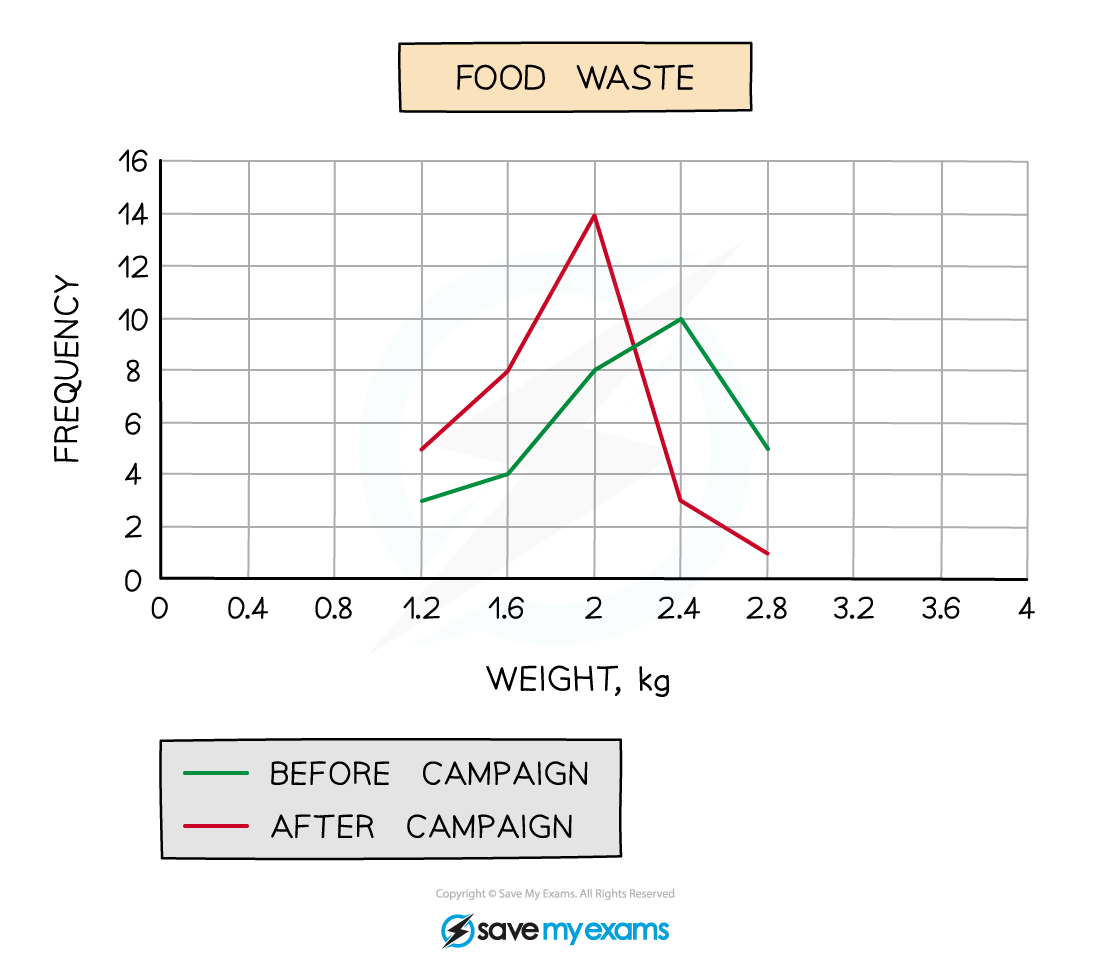
(b) Comment on whether you think the council’s campaign has been successful or not and give a reason why.
Remember to look for average(s) and/or spread
The mode (average) is appropriate in this case.
The council campaign has been successful as the modal amount of waste has decreased from 2.4 kg of food waste per week to 2 kg
Frequency Density
What is frequency density?
Frequency density is given by the formula
This formula is not on the exam formula sheet, so you need to remember it
Frequency density is used with grouped data (i.e. data grouped by class intervals)
It is useful when the class intervals are of unequal width
It provides a measure of how dense data is within its class interval
relative to the width of the interval
For example,
10 data values spread over a class interval of width 20 would have a frequency density of
20 data values spread over a class interval of width 100 would have a frequency density of
As
the data in the first interval is more dense (closer together) than in the second interval
even though the second interval has twice as many data values
How do I calculate frequency density?
In questions it is usual to be presented with grouped data in a table
So add two extra columns to the table
one to work out and write down the class width of each interval
the second to then work out the frequency density for each group (row)
Worked Example
The table below shows information regarding the average speeds travelled by trains in a region of the UK.
The data is to be plotted on a histogram.
Average speed | Frequency |
5 | |
15 | |
28 | |
38 | |
14 |
Work out the frequency density for each class interval.
Add two columns to the table - one for class width, one for frequency density
Use
Writing the calculation in each box helps to maintain accuracy
Average speed | Frequency | Class width | Frequency density |
5 | 40 - 20 = 20 | 5 ÷ 20 = 0.25 | |
15 | 50 - 40 = 10 | 15 ÷ 10 = 1.5 | |
28 | 55 - 50 = 5 | 28 ÷ 5 = 5.6 | |
38 | 60 - 55 = 5 | 38 ÷ 5 = 7.6 | |
14 | 70 - 60 = 10 | 14 ÷ 10 = 1.4 |
Histograms
What is a histogram?
A histogram looks similar to a bar chart, but there are important differences
Bar charts are used for discrete (and possibly non-numerical) data
In a bar chart, the height (or length) of a bar determines the frequency
There are usually gaps between the bars
Histograms are used with continuous data, grouped into class intervals (usually of unequal width)
In a histogram, the area of a bar determines the frequency
This means it is difficult to tell anything simply from looking at a histogram
Some basic calculations will be needed for conclusions and comparisons to be made
There are no gaps between the bars
How do I draw a histogram?
Drawing a histogram first requires the calculation of the frequency densities for each class interval (group)
Use
Exam questions often ask you to finish an incomplete histogram, rather than start with a blank graph
Once the frequency densities are known, the bars (rectangles) for each class interval can be drawn
with widths being measured on the horizontal (x) axis
and the height of each bar (the frequency density) being measured on the vertical (y) axis
As the data is continuous, the bars will be touching
How do I interpret a histogram?
It is important to remember that the frequency density (y-) axis does not tell us frequency
The area of the bar is equal to the frequency
Note that a very simple histogram may have equal class widths
In this case the y-axis may be labelled 'frequency' instead of 'frequency density'
If 'frequency' is on the y-axis, then you can use the heights of the bars to directly determine the frequencies
You may be asked to estimate the frequency of part of a bar/class interval within a histogram
Find the area of the bar for the part of the interval required
Once area is known, frequency can be found as above
You can use histograms for two data sets to compare the data distributions
but only if they have the same class intervals and the same frequency density scales
Examiner Tips and Tricks
Always work out and write down the frequency densities
It is easy to make errors and lose marks by going straight to the graph
Method marks may depend on showing you know to use frequency density rather than frequency
The frequency density axis will not always be labelled
Look carefully at the scale, it is unlikely to be 1 unit to 1 square
Worked Example
A histogram is shown below representing the distances achieved by some athletes throwing a javelin.

There are two classes missing from the histogram. These are:
Distance, | Frequency |
8 | |
2 |
Add these to the histogram.
Before completing the histogram, remember to show clearly you've worked out the missing frequency densities
Distance, | Frequency | Class width | Frequency density |
8 | 70 - 60 = 10 | 8 ÷ 10 = 0.8 | |
2 | 100 - 80 = 20 | 2 ÷ 20 = 0.1 |
Now the bars can be drawn on the histogram
They should stretch along the x-axis from the start to the end of the class interval
The heights will be equal to the frequency densities

Worked Example
The table below and the corresponding histogram show the weight, in kg, of some newborn bottlenose dolphins.
Weight | Frequency |
4 ≤ w < 8 | 4 |
8 ≤ w < 10 | 16 |
10 ≤ w < 12 | 19 |
12 ≤ w < 15 | 12 |
15 ≤ w < 30 |

(a) Use the histogram to complete the table.
The frequency for the 15 ≤ w < 30 class interval is missing
The bar for that class interval on the histogram has a
height (frequency density) of 0.6
width of 30-15 = 15
Rearrange to get
Weight | Frequency |
4 ≤ w < 8 | 4 |
8 ≤ w < 10 | 16 |
10 ≤ w < 12 | 19 |
12 ≤ w < 15 | 12 |
15 ≤ w < 30 | 9 |
(b) Use the table to complete the histogram.
The bar for the 4 ≤ w < 8 class interval is missing
That class interval has a
frequency of 16
width of 10-8 = 2
Use to find the frequency density
Draw a bar with that height on the histogram, between 8 and 10 on the horizontal axis

(c) Estimate the number of dolphins whose weight is greater than 13 kg.
We know from part (a) that there are 9 dolphins in the 15 ≤ w < 30 class interval
So we need to estimate the number of dolphins that are in the interval 13 ≤ w < 15
For 13 ≤ w < 15, the histogram shows that
the frequency density is 4
the width is 15-13 = 2

Now use to estimate the number of dolphins in the 13 ≤ w < 15 interval
(Note that using the histogram in this way is actually a form of linear interpolation)
This is only an estimate because we don't actually know that dolphins are evenly distributed across the entire 12 ≤ w < 15 class interval
Now the total number of dolphins with a weight greater than 13 kg can be estimated
There are approximately 17 dolphins with a weight greater than 13 kg

Unlock more, it's free!
Did this page help you?