Spearman's Rank Correlation Coefficient (Edexcel GCSE Statistics)

Revision Note

Written by: Roger B

Reviewed by: Dan Finlay

Spearman's Rank Basics

What is Spearman’s rank correlation coefficient?

Spearman's rank correlation coefficient measures the strength of the correlation between two data sets
- i.e., to what extent does one always go up when the other one goes up (or always go down when the other one goes up)
- It is not always easy to see this clearly on a scatter diagram
The notation for the Spearman’s rank correlation coefficient of a sample is $r_{S}$
Spearman's rank correlation coefficient is always a number between -1 and 1
- i.e. $- 1 \leq r_{S} \leq 1$
The value of $r_{S}$ tells you about the type and strength of any correlation
- A positive value ( $r_{S} > 0$ ) means there is positive correlation between the data sets
  - An $r_{S}$ value close to 1 means strong positive correlation
- If $r_{S}$ is zero ( $r_{S} = 0$ ), then there is no correlation
- A negative value ( $r_{S} < 0$ ) means there is negative correlation between the data sets
  - An $r_{S}$ value close to -1 means strong negative correlation
- In general, the closer to 1 or -1 that $r_{S}$ is, the stronger the correlation between the data sets

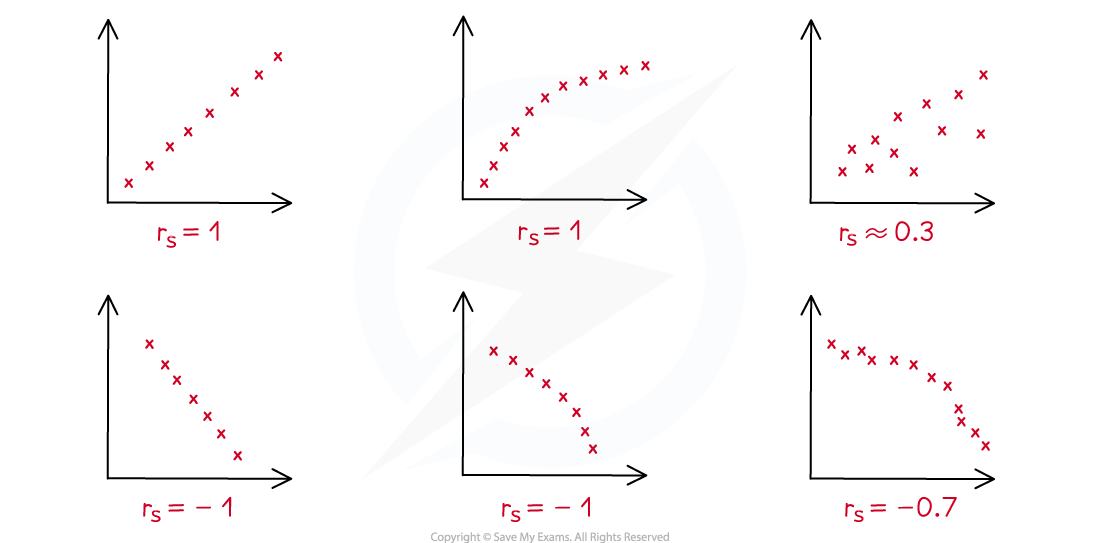
For example, if $r_{S}$ is calculated for the rankings of competitors given by two judges in a competition, then
- $r_{S} = 1$ would mean there was perfect agreement between the two judges' rankings
- $r_{S} = - 1$ would mean the rankings were in completely opposite orders
- $r_{S} = 0$ would mean there was no agreement in the ranks given (but also not consistent disagreement)
Spearman's rank correlation coefficient does not tell you anything about whether or not the data points lie along a straight line
- It only tells you how true it is that one always tends to go up (or down) when the other one goes up

Worked Example

Regina has been watching the judging at a 'best jam' competition at a village fête.

Two judges ranked the 10 different jams that were submitted for the competition.

Regina calculated the Spearman’s rank correlation coefficient for the ranks given by the judges.

She got a value of $- 0.8$ .

(a) What type of correlation is shown by the value $- 0.8$ ? Select one of the three options below:

Negative correlation No correlation Positive correlation

The value is negative, which means negative correlation

Negative correlation

(b) Interpret Regina’s value.

The value is close to -1, which indicates strong negative correlation
This means there was quite a lot of disagreement between the judges' rankings

-0.8 is close to -1, so there is a strong amount of disagreement between the judges' rankings. One tended to like the jams that the other one didn't like, and vice versa.

Calculating Spearman's Rank Correlation Coefficients

How do I calculate a Spearman's rank correlation coefficient?

A Spearman's rank correlation coefficient can be calculated for two sets of data
- This will be bivariate data
  - i.e. the data will occur in pairs of values that 'go together'
  - One set can be thought of as the 'x values'
  - And the other set as the corresponding 'y values'
STEP 1
Rank the values in each set
- Rank the highest x value as 1, the next highest as 2, etc.
  - Then do the same thing for the y values
- It's helpful to add extra rows (or columns) to a table to write down the rankings in
  - along with additional rows (or columns) for the $d$ and $d^{2}$ values calculated in Steps 2 and 3
- You can also start with the lowest value as 1 and rank from lowest to highest
  - But you must do the same thing for both sets!
STEP 2
Calculate the difference $d$ between the ranks for each pair of values
- $d = (rank of x value) - (rank of y value)$
STEP 3
Calculate the squares of the differences between the ranks for each pair of values
- i.e. square each $d$ value to find the corresponding $d^{2}$ value
STEP 4
Find the sum of all the $d^{2}$ values found in Step 3
- This sum of $d^{2}$ values is denoted by $\sum d^{2}$
STEP 5
Calculate the Spearman's rank correlation coefficient $r_{S}$ by using the formula
- $r_{S} = 1 - \frac{6 \sum d^{2}}{n (n^{2} - 1)}$
  - $\sum d^{2}$ is the sum of the differences squared
  - $n$ is the number of data values in each set
  - This formula is on the exam formula sheet, so you don't need to remember it

Examiner Tips and Tricks

Remember that Spearman's rank correlation coefficient is calculated from the rankings of the data values
- not from the data values themselves
Your calculator may be able to calculate a Spearman's rank correlation coefficient directly from lists of the rankings
- An answer using this sort of calculator function will be accepted on the exam

Worked Example

Rex was watching the bonnie pet judging competition at a village fête.

He wrote down the scores (out of 10) that the judges gave to each of 6 pets, and recorded them in the following table.

Pet	Judge 1 score	Judge 2 score
A	9	7.5
B	4.5	6
C	7.5	5.5
D	6	9.5
E	7	10
F	8.5	9

Work out Spearman's rank correlation coefficient for the two judges' scorings, giving your answer correct to 3 decimal places.

First of all, rank the scores in each judge's list
Note that each list is ranked separately
Here we will let '1' be the highest score in each list, and rank from highest to lowest
(You could also call the lowest '1' and rank from lowest to highest, as long as you do that for both lists)

Pet	Judge 1 score	Judge 1 rank	Judge 2 score	Judge 2 rank
A	9	1	7.5	4
B	4.5	6	6	5
C	7.5	3	5.5	6
D	6	5	9.5	2
E	7	4	10	1
F	8.5	2	9	3

Now calculate the differences by subtracting each Judge 2 rank from the corresponding Judge 1 rank

Pet	Judge 1 score	Judge 1 rank	Judge 2 score	Judge 2 rank	d
A	9	1	7.5	4	1-4=-3
B	4.5	6	6	5	6-5=1
C	7.5	3	5.5	6	3-6=-3
D	6	5	9.5	2	5-2=3
E	7	4	10	1	4-1=3
F	8.5	2	9	3	2-3=-1

Now square those to find the d² values

Pet	Judge 1 score	Judge 1 rank	Judge 2 score	Judge 2 rank	d	d²
A	9	1	7.5	4	1-4=-3	(-3)²=9
B	4.5	6	6	5	6-5=1	1²=1
C	7.5	3	5.5	6	3-6=-3	(-3)²=9
D	6	5	9.5	2	5-2=3	3²=9
E	7	4	10	1	4-1=3	3²=9
F	8.5	2	9	3	2-3=-1	(-1)²=1

Find the sum of the d² values

$9 + 1 + 9 + 9 + 9 + 1 = 38$

Now use $r_{S} = 1 - \frac{6 \sum d^{2}}{n (n^{2} - 1)}$
There are 6 scores in each list, so $n = 6$

$\begin{array}{rcl} r_{S} & = & 1 - \frac{6 (38)}{6 (6^{2} - 1)} \\ = & 1 - \frac{228}{210} \\ = & - \frac{3}{35} \\ = & - 0.085714 . . . \end{array}$

Round to 3 decimal places

-0.086

Last updated: 16 April 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Next topic

Did this page help you?

Spearman's Rank Correlation Coefficient (Edexcel GCSE Statistics)

Revision Note

Spearman's Rank Basics

What is Spearman’s rank correlation coefficient?

Worked Example

Calculating Spearman's Rank Correlation Coefficients

How do I calculate a Spearman's rank correlation coefficient?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay