The Normal Distribution (Edexcel GCSE Statistics): Revision Note
Exam code: 1ST0
Characteristics of the Normal Distribution
What is a normal distribution?
A normal distribution is a probability distribution that can be used with continuous quantities
The distribution is symmetrical and bell-shaped about the mean
The mean, median, and mode are all equal
The notation for a normal distribution is
is the mean of the distribution
is called the variance of the distribution
it is a measure of how spread out the data is
it is equal to the standard deviation (
) squared
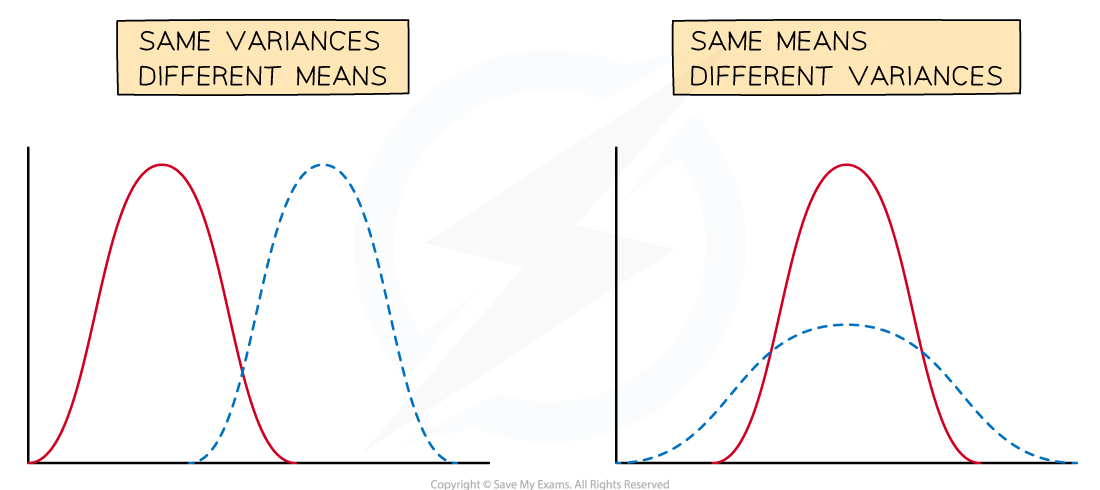
If the mean changes but the standard deviation (or variance) stays the same
then the shape of the distribution stays the same
If the standard deviation (or variance) increases but the mean stays the same then the distribution is stretched out horizontally
A small standard deviation (small variance) means a tall curve with a narrow centre
A large standard deviation (large variance) leads to a short curve with a wide centre
When is a normal distribution a suitable model for a distribution of data?
To use a normal distribution to model a distribution of data, the following must be true
The data must be continuous
e.g. height or weight (in the real world, heights and weights of populations are often normally distributed)
The distribution must be symmetrical and bell-shaped
Most data points near the middle
Decreasing evenly to right and left
The mean, median and mode must be approximately equal
They don't need to be exactly equal, but should be close
This means that a normal distribution is not appropriate for skewed data
How are the data points distributed in a normal distribution?
For a normal distribution
The mean (and mode and median) is μ
The standard deviation is
Remember that standard deviation is the square root of the variance
Of all the data values:
Approximately 68% (just over two thirds) of the data lies within one standard deviation of the mean (
)
Approximately 95% of the data lies within two standard deviations of the mean (
)
Nearly all of the data (99.7%) lies within three standard deviations of the mean (
)
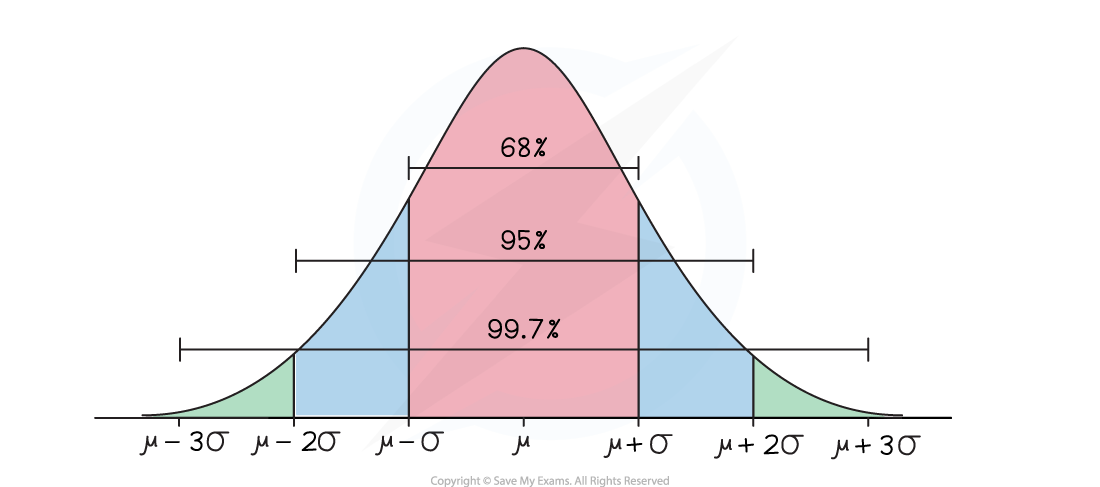
Because the distribution is symmetrical, those regions can be divided into equal halves
Approximately 34% (just over one third) of the data lies
between
and
or between
and
Approximately 47.5% of the data lies
between
and
or between
and
Nearly half the data (49.9%) lies
between
and
or between
and
Note that values more than 3 standard deviations from the mean are very unusual
Such extreme values are considered to be outliers
Examiner Tips and Tricks
Be sure to know the conditions for when a normal distribution is a suitable model
There will often be a question part about this in a normal distribution question
Worked Example
The information from collected data has been used to model the heights of girls and boys in UK Sixth Form colleges.
The graphs below give information about these models.
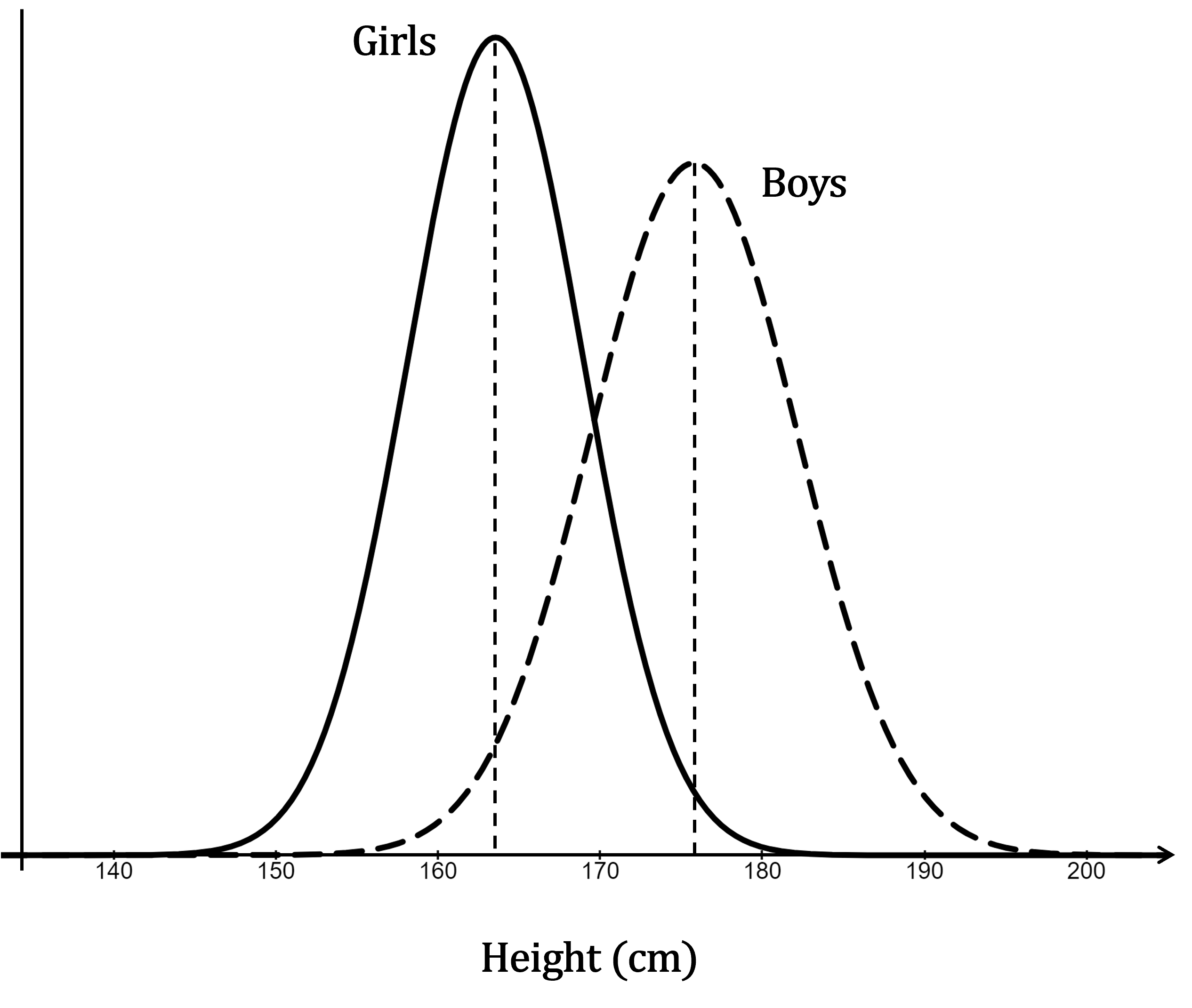
(a) Write down the name of the distribution that is suggested by each of these graphs.
The graphs are symmetrical and bell-shaped, so the normal distribution is suggested
Normal distribution
(b) Comment on the difference between the means of these two distributions.
Remember, the mean is at the centre of a normal distribution's bell-shaped curve
The centre of the 'Boys' curve is further to the right, so that distribution has the higher mean
Don't be fooled by the fact that the 'Girls' curve is higher in the middle!
That just means that the girls' distribution is less spread out than the boys' distribution (so more data values near the middle, and less to the sides)
The boys have a higher mean height (about 176 cm) than the girls (about 164 cm)
The data for the girls' heights has a mean of 163.6 cm and a standard deviation of 5.4 cm.
The data for the boys' heights has a mean of 175.8 cm, and a standard deviation of 6.4 cm.
(c) Calculate an estimate for the percentage of girls that have a height between 158.2 cm and 169.0 cm.
158.2 cm and 169.0 cm are one standard deviation on either side of the mean:
In a normal distribution, about 68% of values lie within that interval
68%
(d) Calculate an estimate for the percentage of boys that have a height greater than 163.0 cm.
163.0 cm is two standard deviations below the mean:
In a normal distribution, 47.5% of the data values lie between and
So 47.5% lie between 163.0 cm and 175.8 cm
Also, 50% lie above the mean (because the distribution is symmetrical and the mean is the same as the median)
So 50% lie above 175.8 cm
Add those together to find the percentage greater than 163.0 cm
97.5%

Unlock more, it's free!
Did this page help you?