Probability Diagrams (Edexcel GCSE Statistics)

Revision Note

Written by: Roger B

Reviewed by: Dan Finlay

Sample Space Diagrams

What is a sample space diagram?

In probability, the sample space means all the possible outcomes
- A sample space diagram is a way of showing all these outcomes in a systematic and organised way
In simple situations sample space diagram can just be a list
- For flipping a coin, the sample space is: Heads, Tails
  - the letters H, T can be used
  - For flipping two coins the sample space could be given as: HH, HT, TH, TT (4 possible outcomes)
- For rolling a six-sided dice, the sample space is: 1, 2, 3, 4, 5, 6
  - But for rolling two dice there would be 36 possibilities!
When combining two things a grid can be used to show the sample space
- For example, rolling two six-sided dice and adding their scores
  - A list of all the possibilities would be very long
    - It would be hard to spot if you had missed any possibilities
    - It would be hard to spot any patterns
- Use a grid instead

A sample space diagram for the sum of the numbers gotten on two dice

If you need to combine more than two things you'll probably need to go back to using a list
- For example, flipping three coins (or flipping one coin three times!)
  - In this case the sample space is: HHH, HHT, HTH, THH, HTT, THT, TTH, TTT (8 possible outcomes)

How do I use a sample space diagram to calculate probabilities?

Probabilities can often be found by counting the possibilities you want,
- then dividing by the total number of possibilities in the sample space
For example, in the sample space 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 you can count 4 prime numbers (2, 3, 5 and 7)
- So the probability of getting a prime number is $\frac{4}{10} = \frac{2}{5}$
Or for rolling two dice and adding the results, the possibility diagram above shows there are 5 ways to get '8', and 36 outcomes in total
- So the probability of getting an 8 is $\frac{5}{36}$
But be careful - this counting method only works if all possibilities in the sample space are equally likely
- For a fair six-sided dice: 1, 2, 3, 4, 5, 6 are all equally likely
- For a fair coin: H, T are equally likely
- Winning the lottery: Yes, No. These are not equally likely!
  - You cannot count possibilities here to say the probability of winning the lottery is $\frac{1}{2}$
This method can also be used for finding the probability of an event occurring given that another event has occurred (conditional probability)
- For example when two dice are rolled, you can use the sample space diagram above to find the probability that an individual dice shows a 6, given that the total showing on the two dice is 7
  - count the number of outcomes that sum to 7 (there are 6 of them) - this goes in the denominator
  - count the number of those outcomes in which one of the dice shows a 6 (there are two of these, (1,6) and (6,1)) - this goes in the numerator
  - So the probability is $\frac{2}{6} (= \frac{1}{3})$

Examiner Tips and Tricks

A questions may not say "by drawing a sample space diagram", so you may have to decide to do it on your own

Worked Example

Two fair six-sided dice are rolled.

(a) Find the probability that the sum of the numbers showing on the two dice is an odd number greater than 5, giving your answer as a fraction in simplest form.

Draw a sample space diagram (in this case a grid) to show all the possible outcomes

Circle the possibilities that are odd numbers greater than 5.
(5 is not included!)

A sample space diagram for the sum of the numbers gotten on two dice, with odd numbers greater than 5 circled

Count the number of possibilities that are circled (12) and divide that by the total number of possibilities in the diagram (36)

$\frac{12}{36}$

Finally, simplify your answer

$\frac{12}{36} = \frac{12 \times 1}{12 \times 3} = \frac{1}{3}$

$\frac{1}{3}$

(b) Given that the sum of the numbers showing on the two dice is an odd number greater than 5, find the probability that one of the dice shows the number 2. Give your answer as a fraction in its simplest form.

From part (a) you already know there are 12 ways to get an odd number greater than 5

Now find how many of those ways (i.e., how many of the circled possibilities in the sample space grid) have one of the dice showing the number 2
There are two of these: (2, 5) and (5, 2)
So the probability we are looking for is 2 divided by 12

$\frac{2}{12}$

Finally, simplify your answer

$\frac{2}{12} = \frac{2 \times 1}{2 \times 6} = \frac{1}{6}$

$\frac{1}{6}$

Two-way Tables for Probability

For basic information about Two-way Tables see the 'Two-way Tables & Venn Diagrams' revision note in the 'Tabulation, Diagrams & Representation' topic. Here we are looking at how to use two-way tables to calculate probabilities.

How do I find probabilities from a two-way table?

Consider the data in the following table, on numbers of Year 12 and 13 students studying Spanish and German in a college with 55 students
- Here the 'totals' have all been given
- On an exam you might need to add the totals rows and columns yourself

	Spanish	German	Total
Year 12	15	10	25
Year 13	5	25	30
Total	20	35	55

You can use this to answer probability questions
- If a random student is selected from the whole college, it will be out of 55
  - The probability a student selected from the college studies Spanish and is in Year 12 is $\frac{15}{55}$
  - The probability a student selected from the college studies Spanish is $\frac{20}{55}$
- If a random student is selected from a specific category, the denominator will be that category total
  - The probability a student selected from Year 13 studies Spanish is $\frac{5}{30}$

How do I work with two-way tables and conditional probability?

With two-way tables, conditional probabilities deal with subsets of things in the table
Conditional probability questions are often (but not always!) introduced by the expression 'given that...'
- For example 'Find the probability that a randomly chosen student studies German, given that the student is in Year 12'
- The answer would be the number of 'Year 12 and German' students divided by the total for the 'Year 12' row
Conditional probabilities can be written using the 'straight bar' notation $P (B | A)$
- That is read as 'the probability of B given A'
  - It is the probability that B will happen if A has happened
- For example $P (German | Year 12)$ would be the probability that a student studies German, given that the student is in Year 12
  - i.e. if a Year 12 student has been selected, what is the probability that that student will study German
The following example shows how conditional probabilities can be calculated from a more complicated two-way table

CP Notes fig5, downloadable IGCSE & GCSE Maths revision notes

Examiner Tips and Tricks

If you had to complete a two-way table (or add the 'total' rows and columns), double-check that your numbers are correct
- If there are errors in the table, probabilities calculated from it will be incorrect and you could lose marks

Worked Example

At an art group, children are allowed to choose between colouring, painting, clay modelling and sketching.

A total of 60 children attend and are split into two classes: class A and class B.

The data for the art group is represented in the following two-way table.

	Colouring	Painting	Clay modelling	Sketching	Total
Class A	12	8	2	8	30
Class B	1	12	13	4	30
Total	13	20	15	12	60

A child is selected at random from the art group. Find the probability that the child

(a) chose colouring

A total of 13 children chose colouring, out of 60 students in total

$\frac{13}{60}$

(b) is a member of class B who chose sketching

4 children are in class B and chose sketching
We are still selecting out of 60 children in total

$\frac{4}{60}$

The simplified answer $\frac{1}{15}$ is also accepted, but is not necessary to get full marks

Now the choice is only 'out of' the 30 children in class A
8 children in that class chose painting

$\frac{8}{30}$

The simplified answer $\frac{4}{15}$ is also accepted, but is not necessary to get full marks

(d) is a member of class B, given that the child chose sketching.

Note that this is not the same thing that is asked in part (b)!

The choice here is out of the 12 students who chose sketching
4 of those children are in class B

$\frac{4}{12}$

The simplified answer $\frac{1}{3}$ is also accepted, but is not necessary to get full marks

Venn Diagrams for Probability

For basic information about Venn Diagrams see the 'Two-way Tables & Venn Diagrams' revision note in the 'Tabulation, Diagrams & Representation' topic. Here we are looking at how to use Venn diagrams to calculate probabilities.

How do I find probabilities from Venn diagrams?

For basic probabilities, count the number of items you want and divide by the total number of items

For the Venn diagram shown above,
- The probability of being in A is $\frac{12 + 4}{12 + 4 + 21 + 8} = \frac{16}{45}$
  - There are 16 elements in A out of 45 in total
- The probability of being in both A and B is $\frac{4}{45}$
  - There are 4 elements in A and B (the 'overlap')
- The probability of being in A, but not B, is $\frac{12}{45}$
  - 12 elements are in A but not B

How do I use Venn diagrams with conditional probability?

With Venn diagrams, conditional probabilities deal with subsets of things in the diagram
Conditional probability questions are often (but not always!) introduced by the expression 'given that...'
- For example 'Find the probability that a randomly chosen item is in A and B, given that the item is in B'
- The answer would be the number of 'A and B' items divided by the total number of items in B
  - For the above diagram that would be $\frac{4}{4 + 21} = \frac{4}{25}$
Conditional probabilities can be written using the 'straight bar' notation $P (B | A)$
- That is read as 'the probability of B given A'
  - It is the probability that B will happen if A has happened
- So for the above example we could write $P (A and B | B) = \frac{4}{25}$
  - i.e. if an item from B has been selected, what is the probability that the item will also be in A

Examiner Tips and Tricks

If you had to create the Venn diagram (or fill in some of the numbers), double-check that your numbers are correct
- If there are errors in the Venn diagram, probabilities calculated from it will be incorrect and you could lose marks

Worked Example

In a class of 30 students, students can study Spanish, German, both, or neither.

The data for the class is represented on the following Venn diagram.

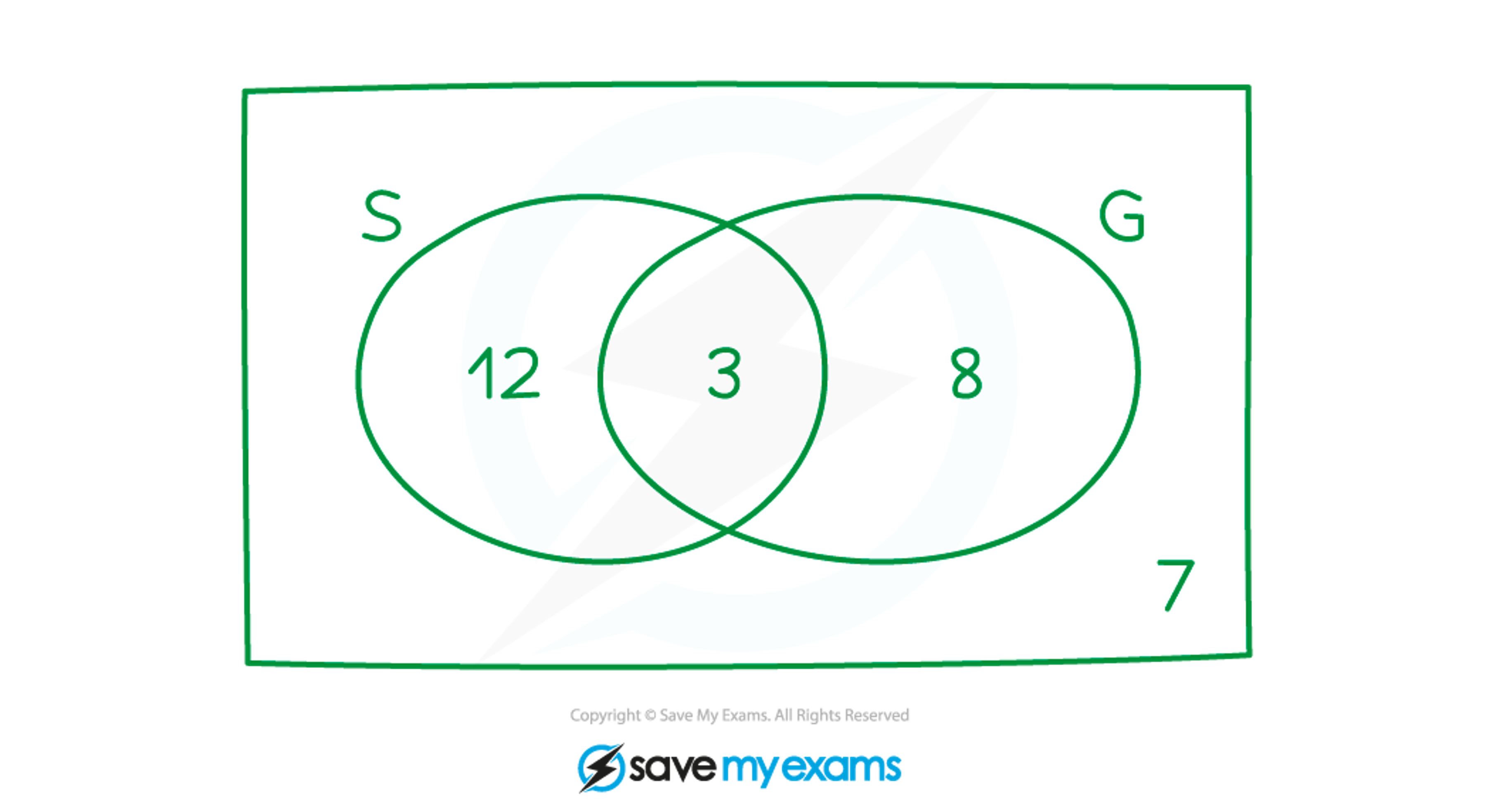
A Venn diagram representing the data for the question

A student is chosen from the class at random. Find the probability that the student

(a) studies German

11 (3+8) students study Spanish, out of 30 students in total

$\frac{11}{30}$

(b) studies Spanish but not German

12 students study Spanish but not German (the part of the 'S' oval that's outside the 'G' oval)
We are still selecting out of 30 students in total

$\frac{12}{30}$

The simplified answer $\frac{2}{5}$ is also accepted, but is not necessary to get full marks

Now the choice is out of the 15 (12+3) students who study Spanish
3 of those students also study German

$\frac{3}{15}$

The simplified answer $\frac{1}{5}$ is also accepted, but is not necessary to get full marks

(d) studies Spanish, given that they do not study German .

Note that this is not the same thing that is asked in part (b)!

There are 19 (12+7) students who do not study German (all the numbers outside the 'G' oval)
12 of those students study Spanish

$\frac{12}{19}$

Venn diagrams are also a context in which probability formulae can be used to answer questions
- See the 'Probability Formulae' revision note to review what these formulae are

Worked Example

The following Venn diagram shows the probabilities associated with two events, $A$ and $B$ .

A Venn diagram showing the probabilities associated with events A and B

It is known that $P (A or B) = 0.32$ .

(a) Find the values of $x$ and $y$ .

To find $x$ we can either use the general addition law $P (A or B) = P (A) + P (B) - P (A and B)$

$\begin{array}{rcl} 0.32 & = & (x + 0.03) + (0.03 + 0.12) - 0.03 \\ 0.32 & = & x + 0.15 \\ 0.17 & = & x \end{array}$

Or you could just notice that $P (A or B)$ has to be the sum of $x$ , 0.03 and 0.12

To find the value of $y$ , remember that these are probabilities
So all of them must add up to 1

$\begin{array}{rcl} 0.17 + 0.03 + 0.12 + y & = & 1 \\ y + 0.32 & = & 1 \\ y & = & 1 - 0.32 \\ y & = & 0.68 \end{array}$

$x = 0.17, y = 0.68$

(b) Show that $A$ and $B$ are independent.

Remember, if $P (A and B) = P (A) \times P (B)$ is true, then A and B are independent

The Venn diagram from the question with all the probabilities written in

$P (A and B) = 0.03 P (A) = 0.17 + 0.03 = 0.2 P (B) = 0.03 + 0.12 = 0.15 P (A) \times P (B) = 0.2 \times 0.15 = 0.03$

$P (A and B) = P (A) \times P (B)$ , so A and B are independent

Use $P (B | A) = \frac{P (A and B)}{P (A)}$

$P (B | A) = \frac{0.03}{0.2} = 0.15$

(You could also use the fact that because $A$ and $B$ are independent, $P (B | A) = P (B)$ )

$P (B | A) = 0.15$

Tree Diagrams

How do I draw a tree diagram?

Tree diagrams can be used for repeated experiments with two outcomes
- The 1st experiment has outcome A or not A
- The 2nd experiment has outcome B or not B
Read the tree diagram from left to right along its branches
- For example, the top branches give A followed by B
  - This is called A and B

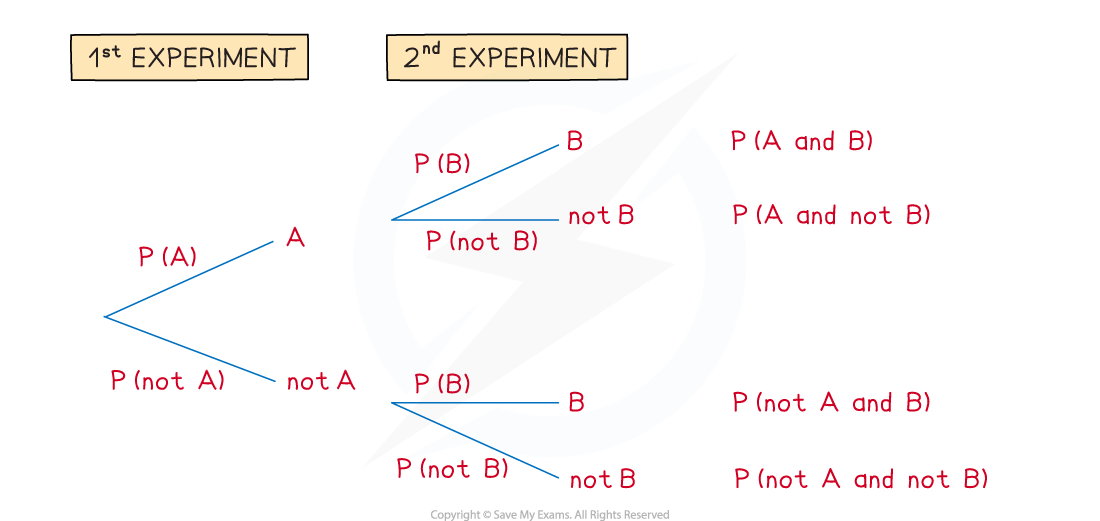
How to set up a tree diagram for two experiments each with two possible outcomes

How do I find probabilities from tree diagrams?

Write the probabilities on each branch
- Remember that P(not A) = 1 - P(A)
  - Probabilities on each pair of branches add to 1
Multiply along the branches from left to right
- This gives P(1st outcome and 2nd outcome)
Add between the separate cases
- For example
  - P('A and B' or 'A and not B') = P(A and B) + P(A and not B)
The probabilities of all possible cases add to 1

How do I use tree diagrams with conditional probability?

Probabilities that depend on a particular thing having happened first in a tree diagram are called conditional probabilities
- For example a team's win and loss probabilities in one game may change depending on whether they won or lost the previous game
  - You might be interested in the probability of them winning a game after losing the previous one
  - This probability will appear in the tree diagram in the set of branches that follow on from 'lose' in the first set of branches
- Or you might be asked to draw or complete a tree diagram for, say, the situation when two counters are drawn from a bag of different coloured counters without replacement
  - The probabilities on the second set of branches will change depending on which branch has been followed on the first set of branches
  - The denominators in the probabilities for the second set of branches will be one less than the denominators on the first set of branches
  - The numerators on the second set of branches will also change depending on what has happened on the first set of branches
  - See the second Worked Example below for an example of this
Conditional probability questions are sometimes (but not always!) introduced by the expression 'given that...'
- For example 'Find the probability that the team win their next game given that they lost their previous game'
Conditional probabilities are sometimes written using the 'straight bar' notation $P (A | B)$
- That is read as 'the probability of A given B'
- For example $P (win | lose)$ would be the probability that the team wins, given that they lost their previous game

Examiner Tips and Tricks

Remember $P (not A) = 1 - P (A)$
Tree diagrams have built-in checks
- the probabilities for each pair of branches should add up to 1
- the probabilities for all final outcomes should add up to 1
When multiplying along branches with fractions, don't cancel fractions in your working - having the same denominator makes them easier to add together!

Worked Example

Lisa drives through two sets of traffic lights on her way to work.

Each set of traffic lights has only two options: green or red.

The probability of the first set of traffic lights being on green is $\frac{5}{7}$ .

The probability of the second set of traffic lights being on green is $\frac{8}{9}$ .

(a) Draw and label a tree diagram. Be sure to show the probabilities of every possible outcome.

Work out the probabilities of each set of traffic lights being on red, R
Use P(red) = 1 - P(green)

$P (1^{st} R) = 1 - P (1^{st} G) = 1 - \frac{5}{7} = \frac{2}{7}$
$P (2^{nd} R) = 1 - P (2^{nd} G) = 1 - \frac{8}{9} = \frac{1}{9}$

Draw the branches (with a label of G or R on the ends)
Write the probabilities above each branch
Calculate probabilities of each outcome by multiplying along the branches from left to right

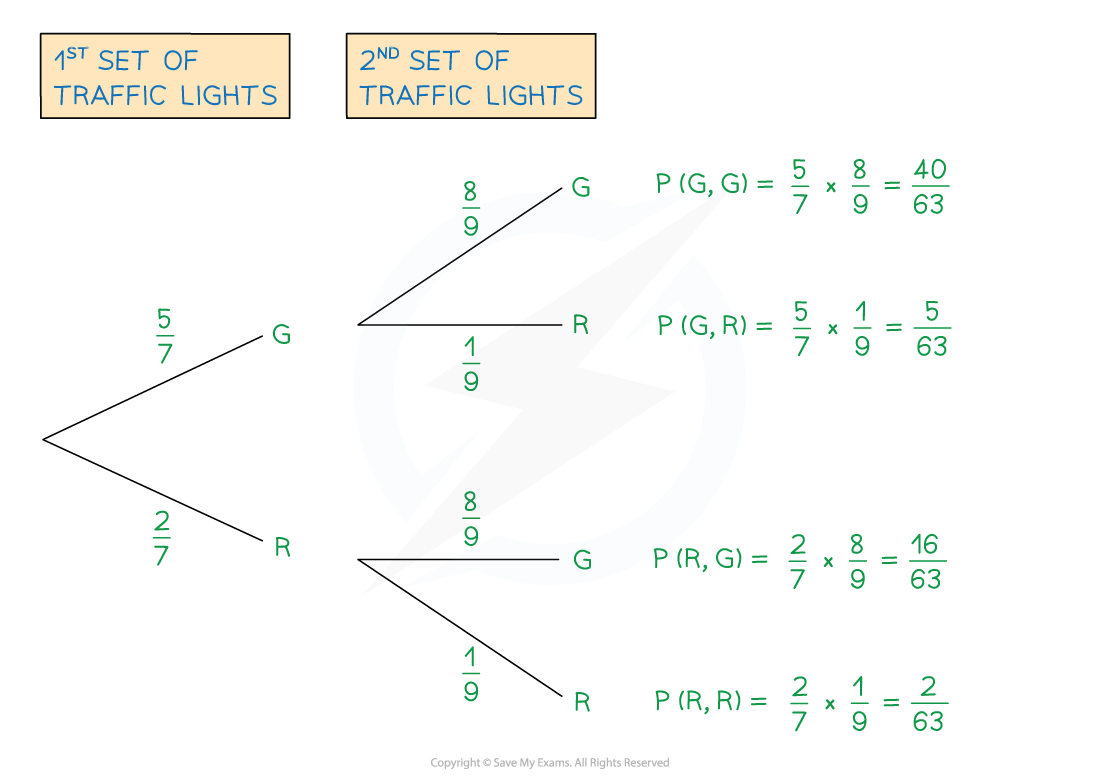
A tree diagram showing different outcomes at traffic lights

(b) Find the probability that both sets of traffic lights are on red.

This is the answer for P(R, R) from the tree diagram

$\frac{2}{63}$

This means the 1st is green and the 2nd is red
Or the 1st is red and the 2nd is green
Or the 1st is red and the 2nd is red ('at least one' could mean both)
Add the probabilities for the separate cases

$P (at least one R) = P (G, R) + P (R, G) + P (R, R) = \frac{5}{63} + \frac{16}{63} + \frac{2}{63} = \frac{23}{63}$

$\frac{23}{63}$

Alternative Method
At least one red means all the possible cases shown except two greens
So P(at least 1 red) = 1 - P(two greens)

$1 - P (G, G) = 1 - \frac{40}{63} = \frac{23}{63}$

$\frac{23}{63}$

Worked Example

Liana has 10 pets: 7 guinea pigs (G) and 3 rabbits (R).

Liana is choosing two pets to feature in her latest online video.

Firstly, she is going to choose one of the pets at random.

Once she has carried that pet to her video studio, she is going to go back and choose a second pet at random, to also feature in the video.

(a) Draw and label a tree diagram including the probabilities of all possible outcomes.

For the 1st pet chosen, there will be a 7/10 probability of choosing a guinea pig, and a 3/10 probability of choosing a rabbit

If the first pet is a guinea pig, there will only be 6 guinea pigs and 3 rabbits left (9 animals total)
So for the second pet the probability of choosing a guinea pig would be 6/9, and probability of choosing a rabbit would be 3/9

If the first pet is a rabbit, there will only be 7 guinea pigs and 2 rabbits left (9 animals total)
So for the second pet the probability of choosing a guinea pig would be 7/9, and probability of choosing a rabbit would be 2/9

Put these probabilities into the correct places on the tree diagram, and then multiply along the branches to find the probabilities for each outcome

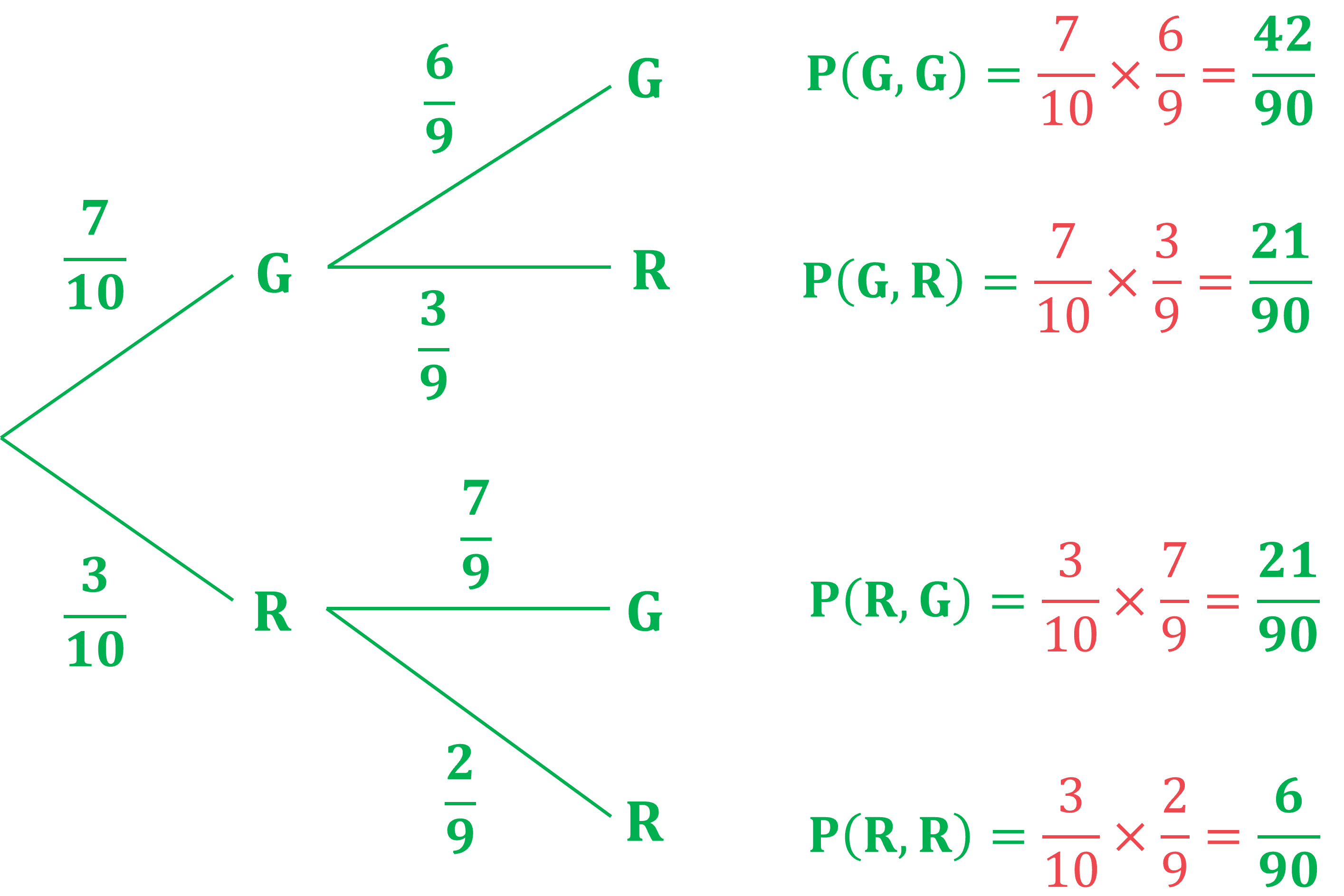
(b) Write down the probability that the second pet is a guinea pig, given that the first pet was a rabbit.

This conditional probability can be done by looking at the branches, without needing the conditional probability formula

This is the probability on the second pet 'G' branch that follows 'R' for the first pet

$\frac{7}{9}$

Using the conditional probability formula would also give this answer

As we have already calculated this probability in the tree diagram, we can just write the answer down

$P (two rabbits) = P (R, R) = \frac{6}{90}$

The simplified answer $\frac{1}{15}$ is also accepted, but is not necessary to get full marks

(d) Find the probability that Liana chooses two different kinds of animal.

This would be "G and R" or "R and G" so we need to add two of the final probabilities

$P (two different kinds) = P (G, R) + P (R, G) = \frac{21}{90} + \frac{21}{90} = \frac{42}{90}$

$P (two different kinds) = \frac{42}{90}$

The simplified answer $\frac{7}{15}$ is also accepted, but is not necessary to get full marks

You could also do this question using 1 - P(both the same)

Last updated: 22 April 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Probability FormulaeNext:The Binomial Distribution

Probability Diagrams (Edexcel GCSE Statistics)

Revision Note

Sample Space Diagrams

What is a sample space diagram?

How do I use a sample space diagram to calculate probabilities?

Two-way Tables for Probability

How do I find probabilities from a two-way table?

How do I work with two-way tables and conditional probability?

Venn Diagrams for Probability

How do I find probabilities from Venn diagrams?

How do I use Venn diagrams with conditional probability?

Tree Diagrams

How do I draw a tree diagram?

How do I find probabilities from tree diagrams?

How do I use tree diagrams with conditional probability?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

The Collection of Data

Planning & Types of Data

Planning an Enquiry

Types of Data

Population, Sampling & Collecting Data

Population & Sampling

Collecting Data

Processing, Representing & Analysing Data

Tabulation, Diagrams & Representation

Bar Charts, Line Graphs & Pictograms

Pie Charts

Stem & Leaf Diagrams

Two-way Tables & Venn Diagrams

Population Pyramids

Choropleth Maps

Cumulative Frequency Charts

Box Plots

Histograms & Frequency Polygons

Selecting & Interpreting Data Representations

Measures of Central Tendency

Mode, Median & Arithmetic Mean

Mode & Mean from Grouped Data

Linear Interpolation

Transforming Data

Other Types of Mean

Measures of Dispersion

Quartiles & Percentiles

Types of Range

Standard Deviation

Outliers

Using Summary Statistics

Using Measures of Central Tendency

Using Measures of Dispersion

Skewness

Index Numbers & Rates of Change

Index Numbers

Rates of Change

Scatter Diagrams & Correlation

Scatter Diagrams & Correlation

Lines of Best Fit & Regression Lines

Spearman's Rank Correlation Coefficient

Pearson's Product Moment Correlation Coefficient (PMCC)

Time Series

Time Series Graphs

Moving Averages

Identifying & Interpreting Trends in Data

Quality Assurance & Estimation

Quality Assurance

Estimation from Statistical Data

Probability

Probability Basics

Probabilities & Data

Risk & Bias

Probability Formulae

Probability Diagrams

Probability Distributions

The Binomial Distribution

The Normal Distribution

Author: Roger B

Author: Dan Finlay