Probabilities & Data (Edexcel GCSE Statistics)

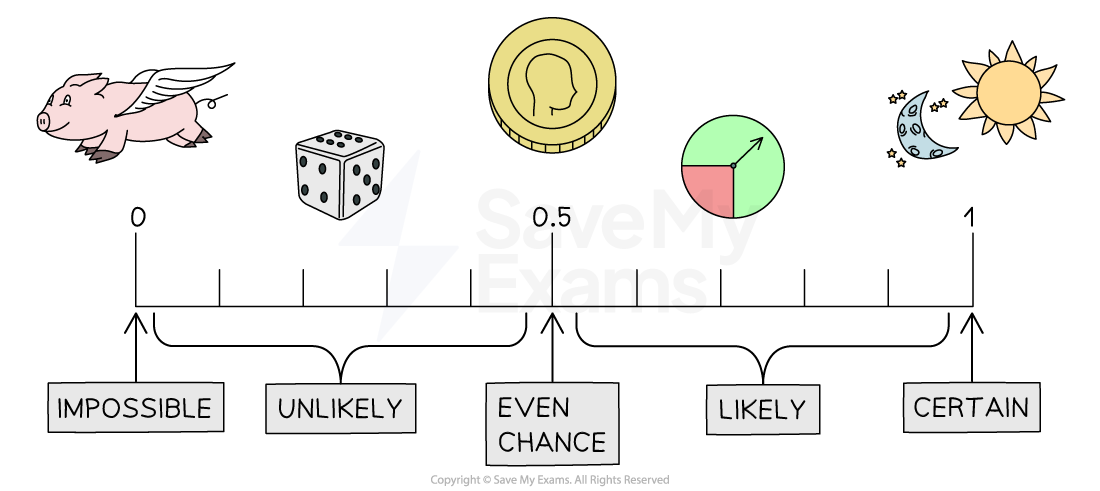
The Probability Scale & Basic Probabilities

What is the probability scale?

• Probability describes the likelihood of something happening

  • In real-life you might use words such as impossible, unlikely and certain

  • In maths we use the probability scale to describe probability

• On the probability scale likelihood is measured by a number between 0 and 1

  • 0 means impossible (i.e. it will never happen)

    • a pig will grow wings and fly

  • Between 0 and 0.5 means unlikely

    • getting a '6' when you roll a fair 6-sided dice

    • getting a '6' when you choose a number between one and a million at random can be described as very unlikely

  • 0.5 means even chance (i.e. it happens 50% of the time)

    • getting 'heads' when you flip a fair coin

  • Between 0.5 and 1 means likely

    • a spinner that is three quarters green landing on green

    • not getting a '6' when you choose a number between one and a million at random can be described as very likely

  • 1 means certain (i.e. it will always happen)

    • the sun will rise tomorrow morning

• Probabilities can be given as fractions, decimals or percentages

How do I calculate basic probabilities?

• An outcome is a single possible result of a trial

  • For example:

    • a dice lands on 6

    • a dice lands on 5

• If all possible outcomes are equally likely then the probability for each outcome is the same

  • The probability for each outcome is

  • If there are 50 marbles in a bag then the probability of selecting a specific one is

• An event is an outcome or a collection of outcomes

  • For example:

    • a dice lands on a six (one outcome)

    • a dice lands on an even number (a collection of outcomes)

  • Events can be referred to by capital letters

    • e.g. event A might be 'a dice lands on an odd number'

    • The probability of event A occurring can be written as P(A)

• If all possible outcomes are equally likely then the probability of an event can be calculated by dividing the number of 'successful' outcomes by the total number of possible outcomes

  •  

  • A 'successful' outcome is an outcome belonging to the event

    • e.g. for the event 'a dice lands on an even number'

    • '2', '4' and '6' are all successful outcomes

  • If there are 50 marbles in a bag and 20 are blue, then the probability of selecting a blue marble is

    • The probability of selecting a particular blue marble is still

• A probability worked out this way is sometimes known as a theoretical probability

• The word 'fair' is used to indicate equally likely outcomes

  • e.g. for tossing a fair coin, heads and tails are equally likely

  • or for rolling a fair dice, each number on the dice is equally likely

Expected Frequency

What is expected frequency?

• Expected frequency refers to the number of times you would expect a particular event to occur 

• It is found by multiplying the probability of the event by the number of trials

  • 

    • e.g. if you flip a fair coin 100 times

    • you would expect 0.5 × 100 = 50 heads

Estimating Probabilities from Data

How can I estimate probabilities from data?

• In the real world it can be difficult or impossible to find out the exact probability of an event occurring

  • By conducting an appropriate experiment we can estimate the probability

    • e.g. to estimate the probability of a chicken egg having two yolks

    • we can collect a sample of chicken eggs and see how many have two yolks

• Each repeat of an experiment is called a trial

  • e.g. each chicken egg tested would count as one trial

    • if a particular egg has two yolks that would be a successful outcome

• To find the estimated probability, divide the number of successful outcomes by the total number trials

  • 

• A probability estimated in this way is known as an experimental probability or relative frequency

How does the number of trials affect an estimated probability?

• Using a larger number of trials will increase the reliability of an estimated probability

  • e.g. using a larger sample of eggs to check for double yolks

  • or rolling a dice a larger number of times to estimate the true probability of getting a 6

• In general

  • the experimental probability will tend towards the true probability

  • as the number of trials is increased

• For example, it is unlikely that you will get exactly 5 heads if you flip a fair coin 10 times

  • But the more and more times you flip it

  • the closer to 50% the total number of heads will tend to become

How can I make predictions using estimated probabilities?

• You can use an estimated probability to calculate an expected frequency

  • e.g. if you flip a biased coin 40 times and get 10 heads, how many heads would you expect when flipping 100 times?

    • The estimated probability is = 0.25 from the first 40 flips

    • 0.25 × 100 = 25, so you would expect to get heads 25 times from 100 throws

• It is possible that you will be asked to make predictions based on a relative frequency diagram

  • This is a type of bar chart that has relative frequencies instead of frequencies on the vertical axis

  • See the Worked Example