Bar Charts, Line Graphs & Pictograms (Edexcel GCSE Statistics) : Revision Note
Bar Charts & Vertical Line Graphs
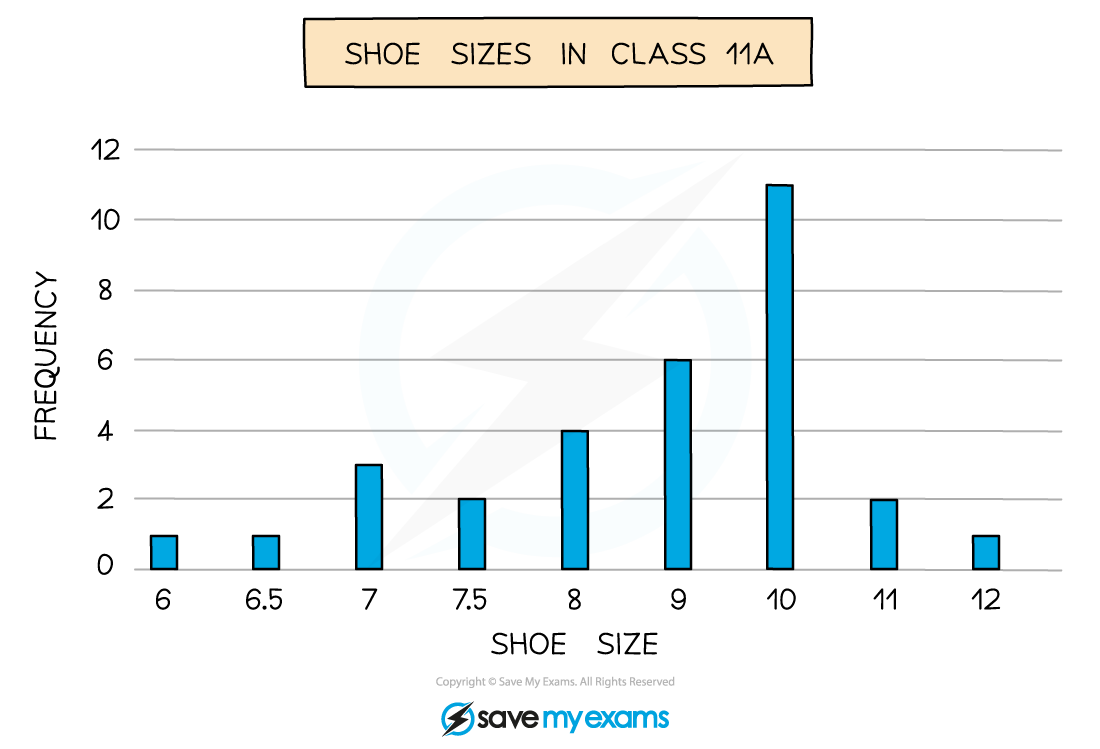
What is a bar chart?
A bar chart is a visual way to represent discrete data
Discrete data is data that can be counted
This can be numerical like shoe sizes in a class
Or non-numerical (categorical) like colours of cars down a road
The horizontal axis shows the different outcomes
The vertical axis shows the frequency
The heights of the bars show the frequency
Bars should be separated by gaps
Bars should have equal widths
What is a dual (comparative) bar chart?
Dual (or comparative) bar charts compare two data sets on one bar chart
The data sets measure the same variable, so use the same scale
The bars are in pairs (side-by-side) for each outcome
e.g. For comparing the shoe sizes of two year groups
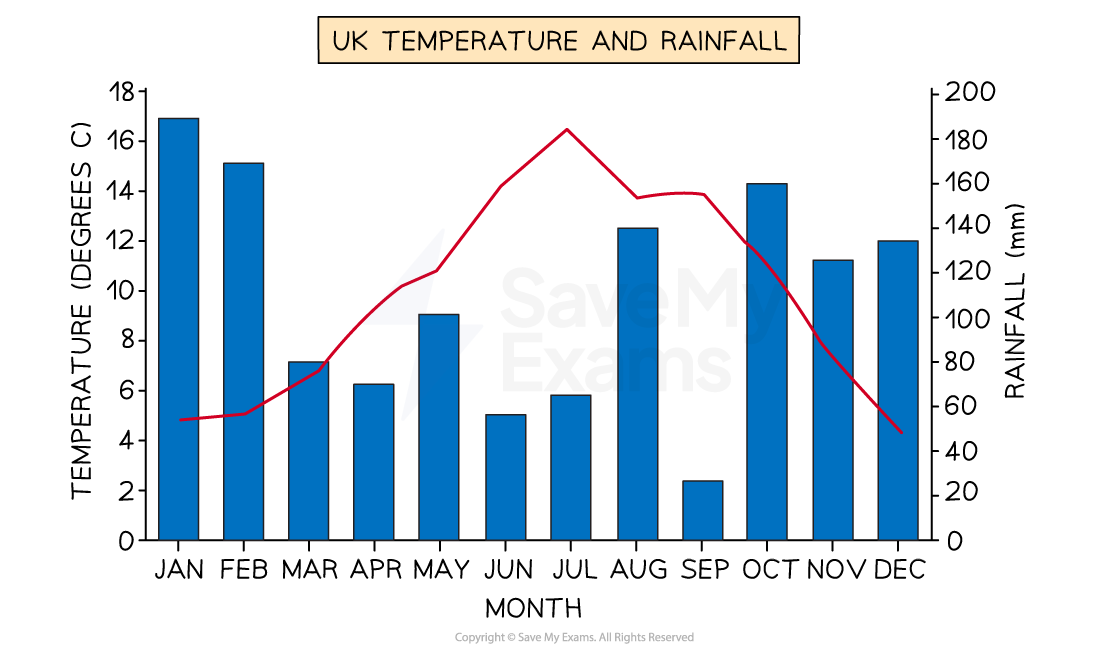
What is a bar-line chart?
A bar-line chart also shows two data sets on one chart
However one data set is represented by a line, and the other by bars
This allows two different variables to be shown, with a different scale for each
e.g. For showing the monthly temperature (as a line) and the monthly rainfall (as bars) across the year for a location
One scale would be in °C, and the other would be in mm
There are also composite bar charts, which are covered in their own section below
What is a vertical line graph?
A vertical line graph (or vertical line chart), is a visual way to represent discrete data
Vertical line graphs are used for numerical data (rather than categorical data)
They are particularly useful when there are lots of different options to show
e.g. Results of a test where scores are given as percentages
Do not confuse these with the line graphs which are used when drawing time series graphs
For those, see the 'Time Series Graphs' revision note
The vertical axis shows the frequency
The horizontal axis shows the different outcomes

You can easily identify the mode (most common value) using a line chart
This will be the outcome with the highest (tallest/longest) line
e.g. In the line chart above, 11 was the modal test score, with a frequency of 7
You can quickly see how the data is spread using a line chart
Lines may be crowded around a particular group of options
This may help identify anomalies or outliers in the data
e.g. In the line chart above you can see
the majority of the test scores, out of 20, were between 7 and 12
one pupil scored 19 out of 20, much higher than anyone else in the class
Examiner Tips and Tricks
If asked to draw a bar chart, find the largest frequency and select a scale which allows it to fit in the space provided
Worked Example
Mr Barr teaches students in Year 7 and Year 8.
He records the number of pets that students in each year have.
His results are shown in the dual bar chart below.
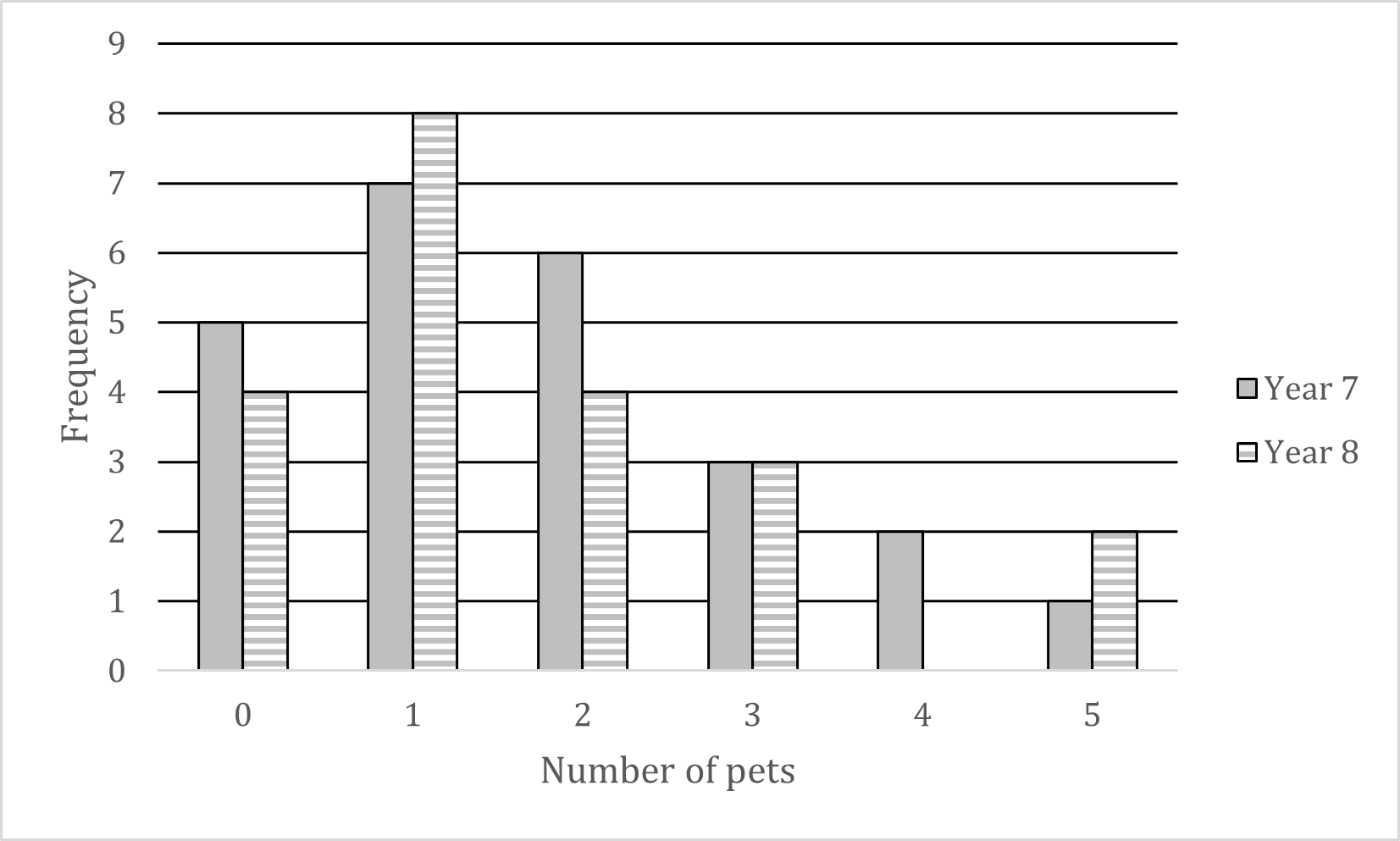
(a) Write down the modal number of pets for his Year 7 students.
The modal number (mode) is the number of pets that occurs the most
Visually, this will be the highest bar for Year 7s
The mode for Year 7 is 1 pet
(b) How many Year 8 students does he teach?
Add up all the heights (frequencies) of the Year 8 bars
4 + 8 + 4 + 3 + 0 + 2 = 21
He teaches 21 Year 8 students
Pictograms
What is a pictogram?
A pictogram is an alternative to a bar chart
It is used in the same situations
There are no axes
Frequency is represented by symbols
A key shows the value of 1 symbol
For example, 1 symbol represents a frequency of 2
Half and quarter symbols are often used

The pictogram above shows the shoe sizes of students in a class
As 1 picture of a shoe represents 2 students
Half a shoe represents 1 student
The number of students with a shoe size of 7, is 3
Composite Bar Charts
What is a composite bar chart?
A composite bar chart shows the total frequency for a category as well as the proportions in each category
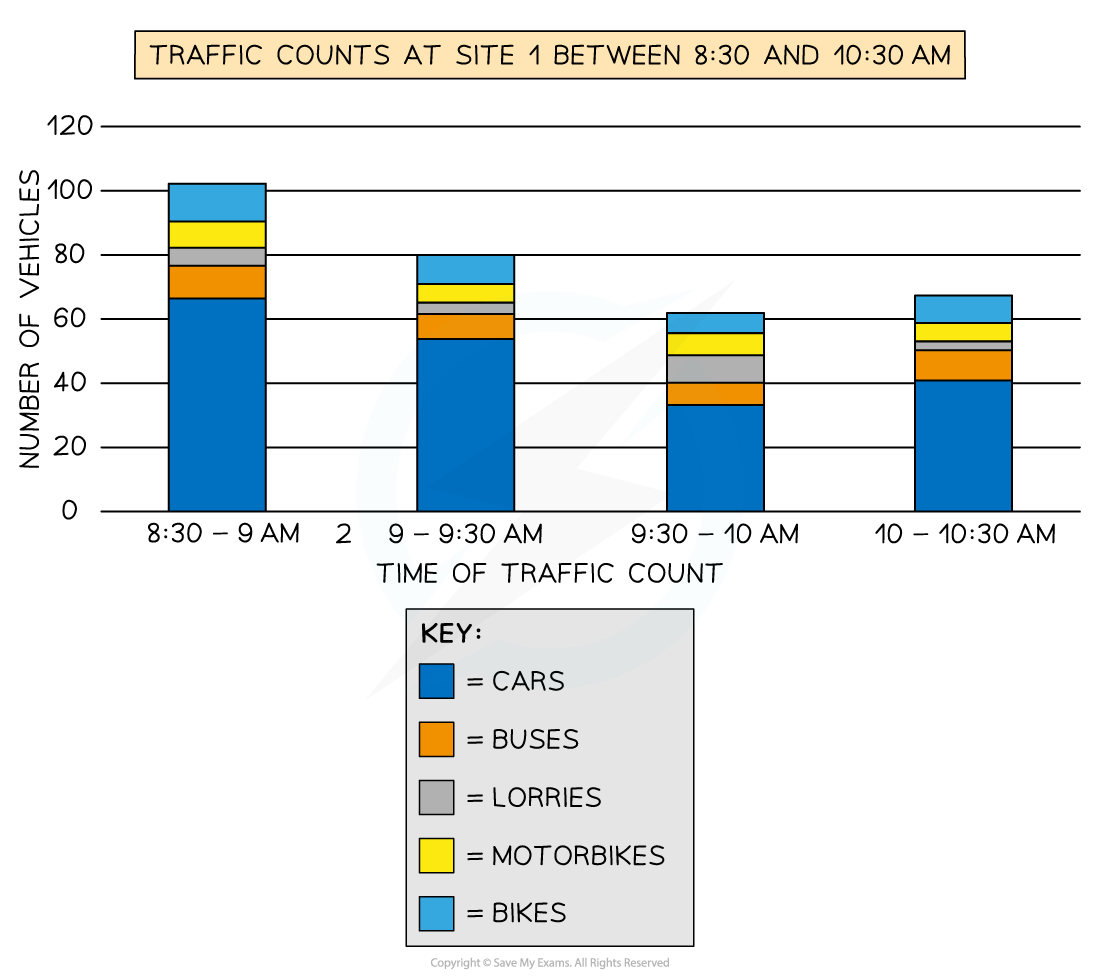
For example, the chart below shows the total number of vehicles passing a location at different times
The overall height of each bar shows the total number of vehicles
The sections within each bar show the proportion of vehicles by type
Be careful - it is just the height of each coloured section which shows the frequency, not the whole bar
e.g. For 9-9:30 am, there are around 10 bikes, not 80
Composite bar charts can reveal more information that a regular bar chart
e.g. The below chart shows the least traffic in total is between 9:30-10 am, but it is also during this time that the greatest number of lorries are present
Examiner Tips and Tricks
It can be useful to annotate each section of the bar with its frequency when working
Worked Example
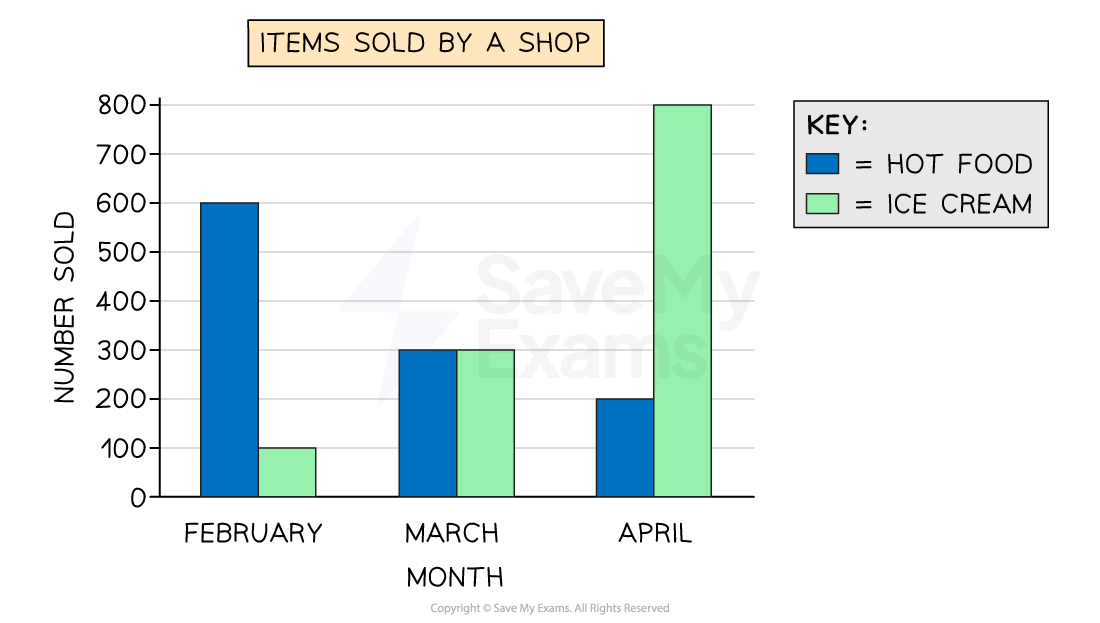
The composite bar chart below shows the number of ice creams and hot food items sold by a shop each month, for three months.
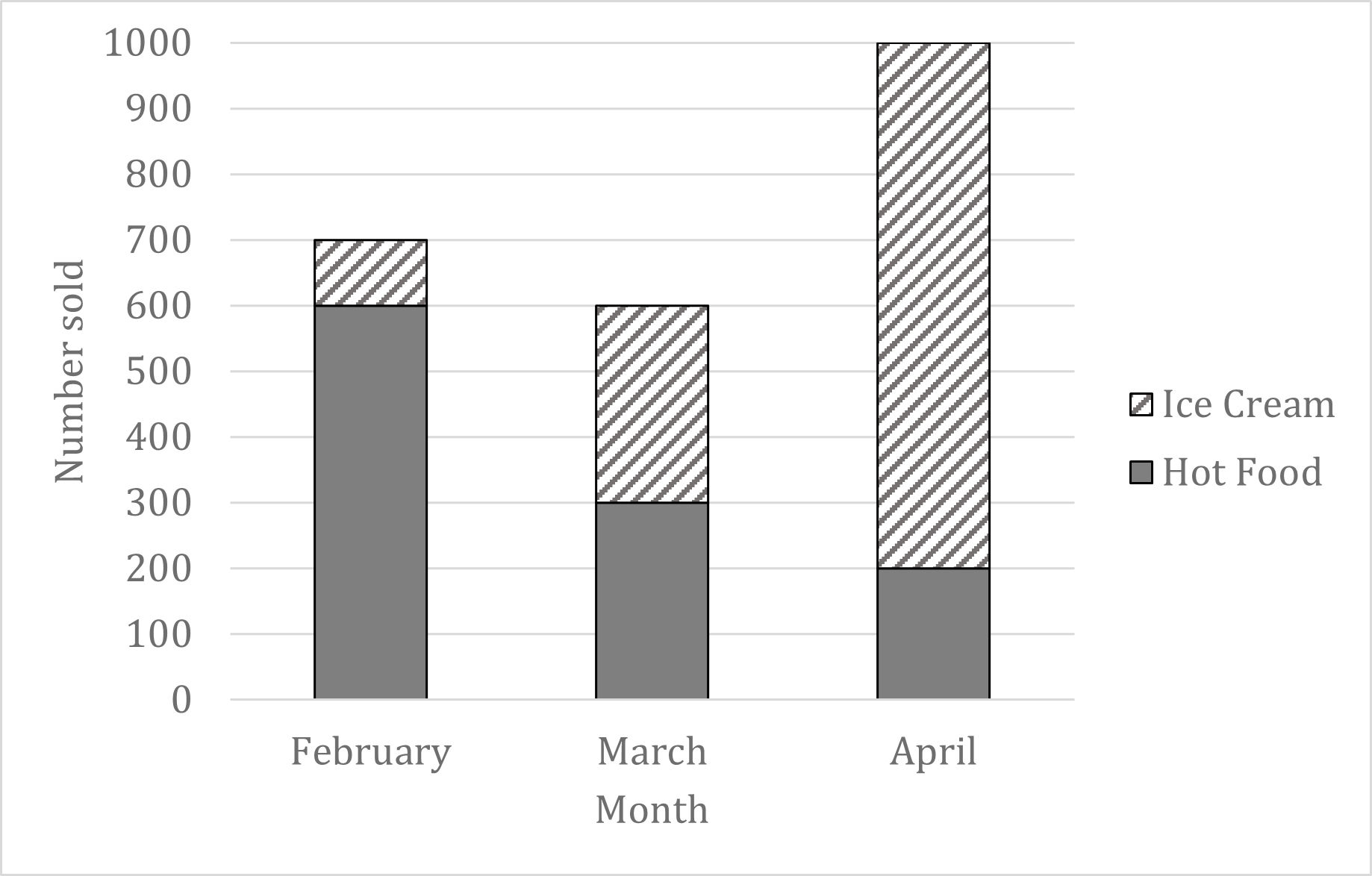
(a) Write down the month in which the most items were sold in total.
The total number of items sold (both ice creams and hot food) is represented by the overall height of the bars
Most items were sold in total in April
(b) Write down the number of ice creams sold in February.
Ice creams are shown by the striped part of the bar
In February, this part of the bar spans from 600 to 700
700 - 600 = 100
In February 100 ice creams were sold
(c) Calculate how many more ice creams were sold in March than in February.
We know that in February 100 ice creams were sold
In March, the striped part of the bar spans from 300 to 600
600 - 300 = 300 ice creams sold in March
Find the difference
300 - 100 = 200
In March 200 more ice creams were sold than in February
(d) Find the total percentage of items sold that were ice cream, across the three months. Give your answer to 1 decimal place.
We need to find the total number of ice creams sold across the three months
We already know that the number of ice creams sold in February was 100, and 300 in March
In April, the striped part of the bar spans from 200 to 1000
1000 - 200 = 800 ice creams sold in April
Find the total number of ice creams sold
100 + 300 + 800 = 1200 ice creams sold in total
We need to find the total number of items sold across the three months
Add up the total heights of all the bars
700 + 600 + 1000 = 2300 items sold in total
Find the number of ice creams sold as a percentage of the total number of items
1200 ÷ 2300 = 0.521739... = 52.1739... %
Round to 1 decimal place
52.2 % of all items sold were ice creams

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

