Investigating the Force-Extension Graph for a Spring (WJEC GCSE Science (Double Award)): Revision Note

Specified Practical: Investigating the Force-Extension Graph for a Spring

Aim of the Experiment

•  This experiment aims to investigate the relationship between the force and extension of a spring F = kx 

  • Also known as Hooke's Law

Variables:

• Independent variable = Force, F

• Dependent variable = Extension, x

• Control variables:

  • Spring with spring constant, k

  • Equipment used and set up

  • Method of taking measurements

Equipment List

Equipment Used for Force and Extension of a Spring Investigation

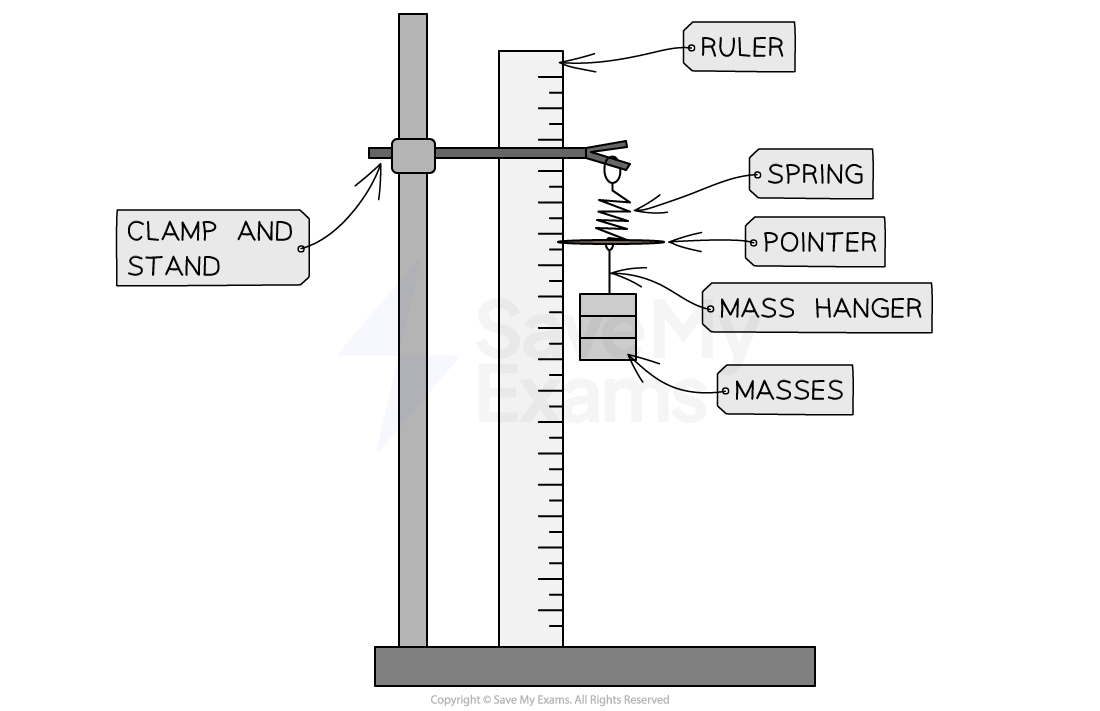
Fixing the ruler to the clamp stand will reduce movement in the ruler and therefore reduce errors in measurement

Method

1. Attach the ruler to the clamp stand, hang the spring, and attach the pointer to the bottom of the spring

2. Measure the initial length of the spring with no masses attached

3. Add the mass hanger (of mass 100 g) and record the length of the spring

4. Remove and repeat 3 times to calculate an average length

5. Subtract the initial length of the spring from the average length to calculate the extension

6. Add a 100 g mass to the mass hanger and record the length of the spring

7. Repeat the process adding an additional 100 g mass each time

An Example Table of Results

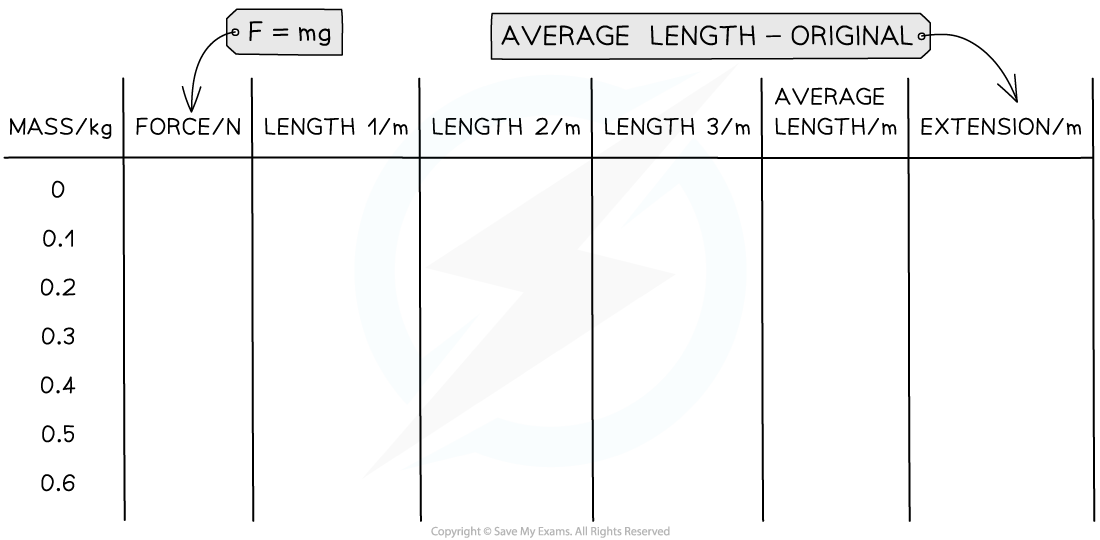
A suitable table of results must contain the calculations for force and extension

A Table of Expected Results

Analysis of Results

• The force, F added to the spring is the weight of the mass

• The weight is calculated using the equation:

W = mg

• Where:

  • W = weight in Newtons (N)

  • m = mass in kilograms (kg)

  • g = gravitational field strength on Earth in Newtons per kg (N/kg)

• The extension of the spring is calculated using the equation:

extension = final length – original length

1. Plot a graph of the force against the extension

2. Draw a line of best fit

3. If the graph has a linear region (a straight line with an increasing gradient), then the force is proportional to the extension and the spring obeys Hooke's Law

An Example Force-Extension Graph for a Spring

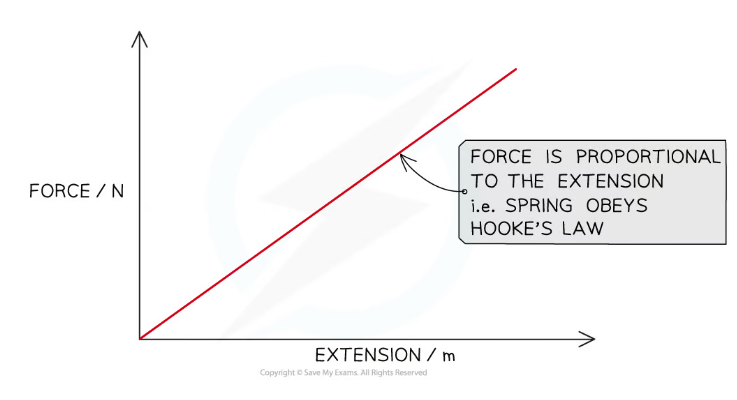
The graph is a straight line that goes through the origin which shows that the extension of the spring is directly proportional to the force applied 

Evaluating the Experiment

Systematic Errors:

• Make sure the measurements on the ruler are taken at eye level to avoid parallax error

Random Errors:

• The precision of the experiment is improved with the use of a pointer at the bottom of the spring

• Wait a few seconds for the mass to become stationary after it is added, before taking the readings for its length

• Check that the spring has not gone past its limit of proportionality otherwise, it has been stretched too far and will no longer obey this relationship

• Make sure the measurements are taken from the same point on the bottom of the spring every time

Safety Considerations

• Wear goggles during this experiment in case the spring snaps

• Stand up while carrying out the experiment making sure no feet are directly under the masses

• Place a mat or a soft material below the masses to prevent any damage in case they fall

• Use a G clamp to secure the clamp stand to the desk so that the clamp and masses do not fall over

  • As well as this, place each mass carefully on the hanger and do not pull the spring too hard so it breaks or pulls the apparatus over

• Do not pull the masses down further with your hand

• Do not exceed the maximum load of the spring, roughly 700 g