Calculating Half-Life (WJEC GCSE Science (Double Award)): Revision Note

Calculating Half-Life

• Aside from calculating the half-life of an isotope, calculations involving half-life might involve

  • Predicting the amount remaining, or activity, of a sample after a certain time

  • Calculating the age of a sample

Predicting the amount of sample remaining

• After each half-life, the amount of isotope remaining decreases by half

• Half-life can also be represented in a table

• As the number of half-lives increases, the proportion of the isotope remaining halves

Number of half-lives vs proportion of isotope remaining

Calculating the age of a sample

• Carbon-14 can be used to estimate the age of organic samples in a process called carbon dating

• This is done by measuring the proportion of carbon-14 to the proportion of the stable isotope carbon-12

  • The proportion of carbon-14 is constant in living organisms as carbon is continuously replaced during the period they are alive

  • When an organism dies, the activity of the carbon-14 begins to fall

  • So, the amount of carbon-14 remaining in a sample can be compared to the amount a living tissue contains to determine the approximate age of the sample

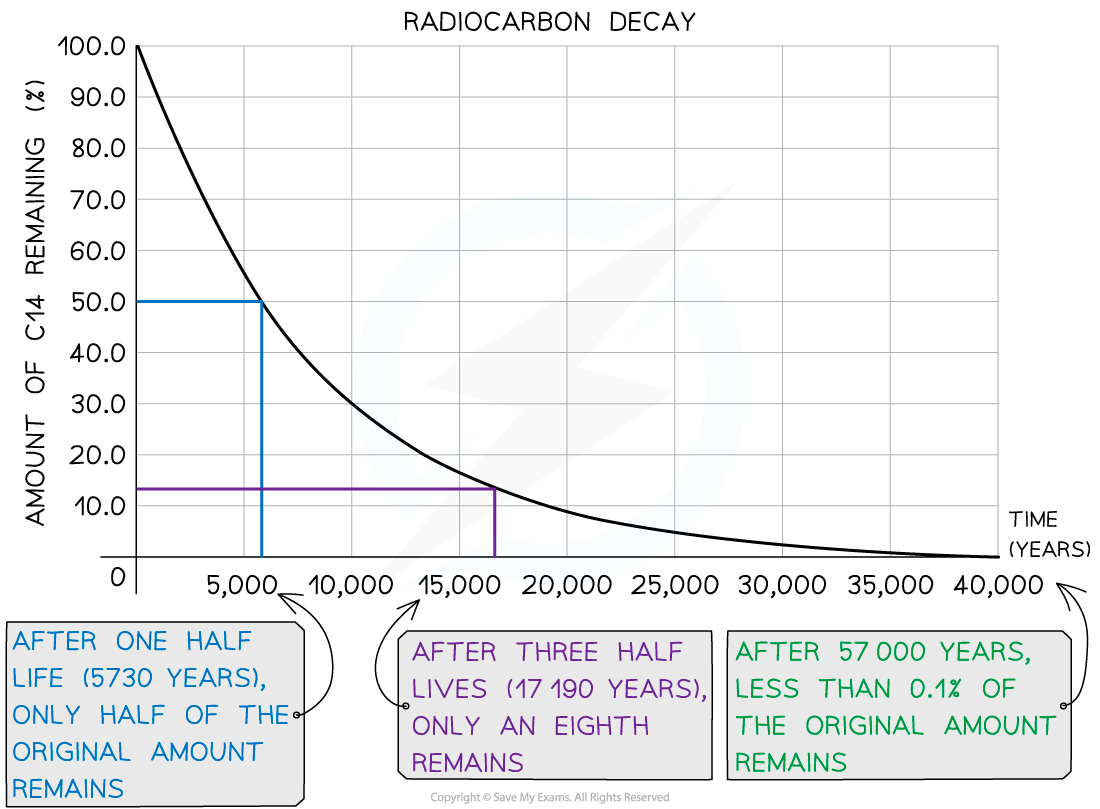
• Carbon-14 has a half-life of around 5700 years

  • After 5700 years, there would be 50% of the original amount of carbon-14 remaining

  • After two half-lives, or 11 400 years, there would be just 25% of the carbon-14 remaining

Decay Curve for Carbon-14