Velocity-Time Graphs (WJEC GCSE Science (Double Award)) : Revision Note
Velocity-Time Graphs
A speed-time graph shows how the speed of an object varies with time
A velocity-time graph shows how the speed of an object moving in a certain direction varies with time
Acceleration & Deceleration on a Speed-Time Graph
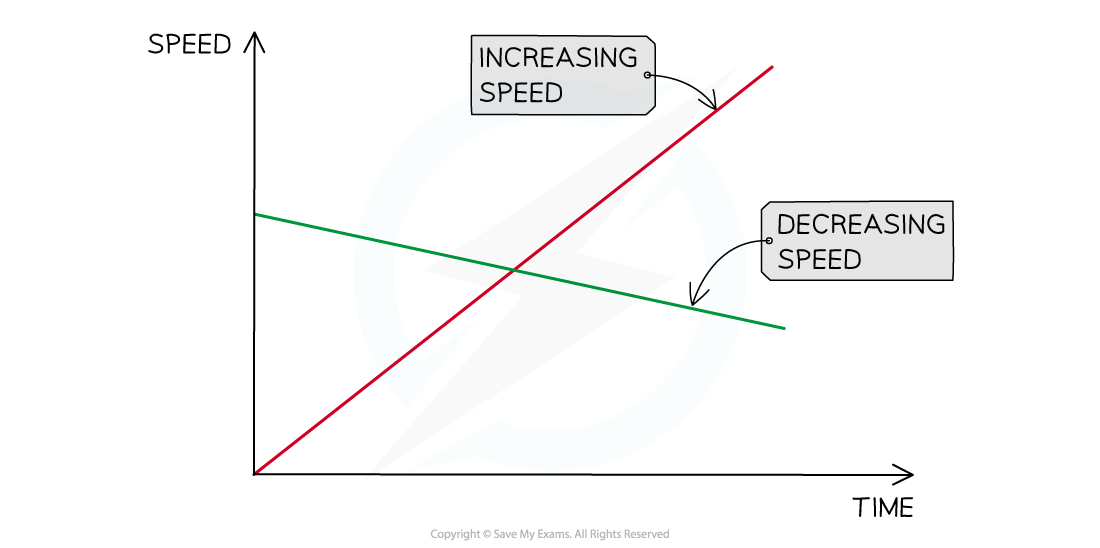
The red line shows the speed of an object increasing over time, whilst the green line shows the speed of an object decreasing over time
Acceleration on a Velocity-Time Graph
The slope of the line represents the magnitude of acceleration
A steep slope means large acceleration (or deceleration)
The object's velocity changes very quickly
A gentle slope means small acceleration (or deceleration)
The object's velocity changes very gradually
A flat line means the acceleration is zero
The object is moving with a constant velocity
A constant velocity means a constant speed in a straight line
Interpreting Gradients on a Velocity-Time Graphs
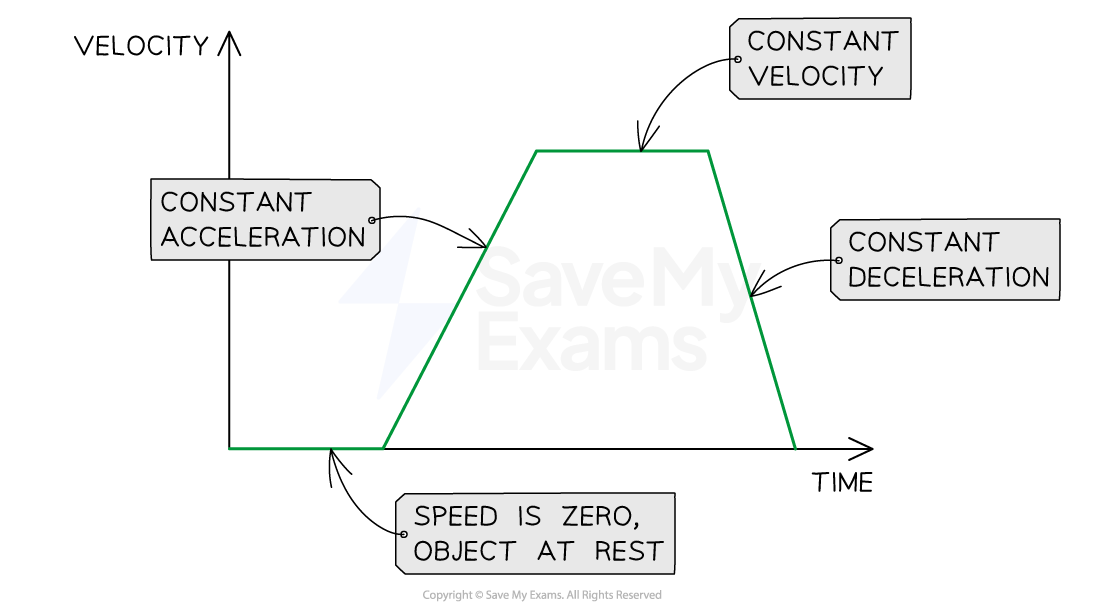
This image shows how to interpret the slope of a velocity-time graph
The acceleration of an object can be calculated from the gradient of a velocity-time graph
Calculating Gradient of a Velocity-Time Graph
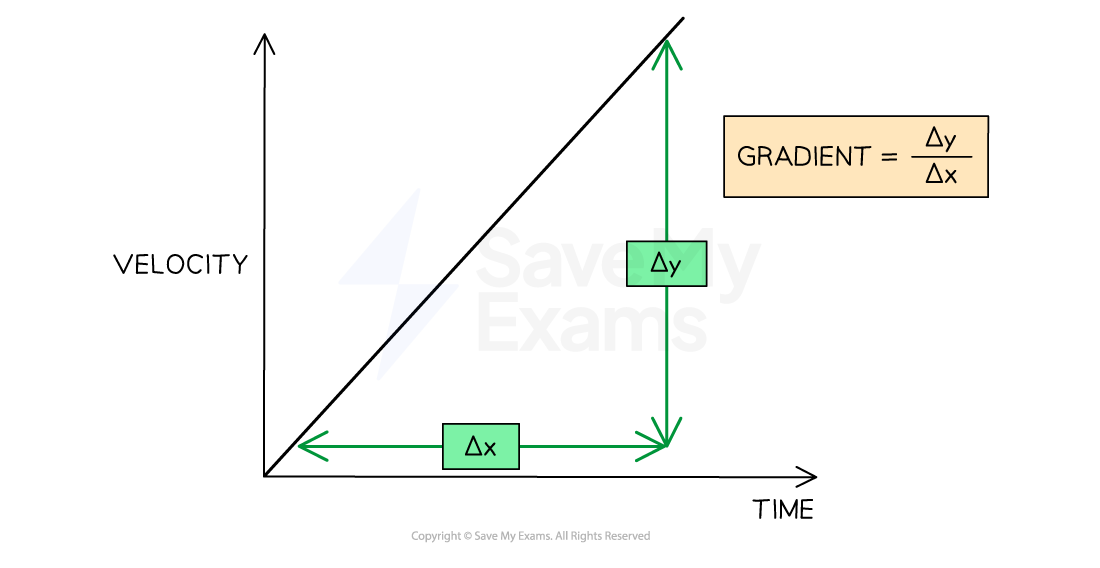
The gradient of a velocity-time graph can be found by dividing the change in velocity by the change in time
Worked Example
A cyclist is training for a cycling tournament.
The velocity-time graph below shows the cyclist's motion as they cycle along a flat, straight road.

(a) In which section (A, B, C, D, or E) of the velocity-time graph is the cyclist's acceleration the largest?
(b) Calculate the cyclist's acceleration between 5 and 10 seconds.
Answer:
Part (a)
Step 1: Recall that the slope of a velocity-time graph represents the magnitude of acceleration
The slope of a velocity-time graph indicates the magnitude of acceleration
Therefore, the only sections of the graph where the cyclist is accelerating are sections B and D
Sections A, C, and E are flat; in other words, the cyclist is moving at a constant velocity (therefore, not accelerating)
Step 2: Identify the section with the steepest slope
Section D of the graph has the steepest slope
Hence, the largest acceleration is shown in section D
Part (b)
Step 1: Recall that the gradient of a velocity-time graph gives the acceleration
Calculating the gradient of a slope on a velocity-time graph gives the acceleration for that time period
Step 2: Draw a large gradient triangle at the appropriate section of the graph
A gradient triangle is drawn for the time period between 5 and 10 seconds
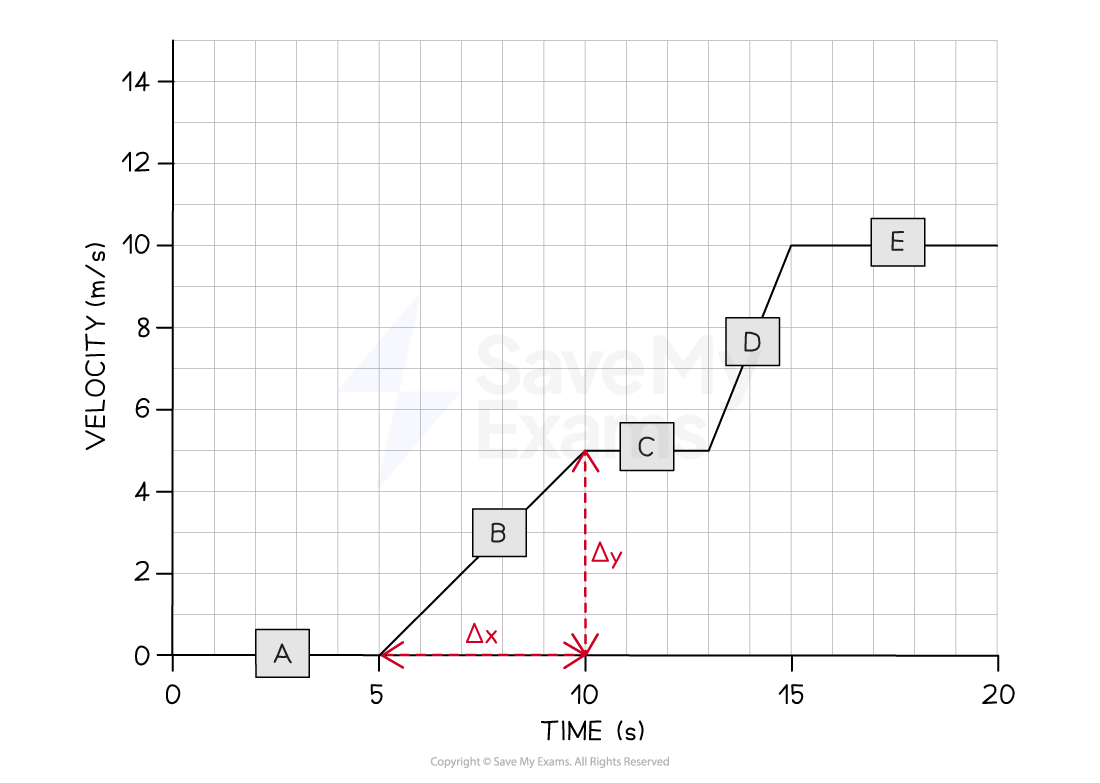
Step 3: Calculate the size of the gradient and state this as the acceleration
The acceleration is given by the gradient, which can be calculated using:
Therefore, the cyclist accelerated at 1 m/s2 between 5 and 10 seconds
Examiner Tips and Tricks
Use the entire slope, where possible, to calculate the gradient. Examiners tend to award credit if they see a large gradient triangle used.
Remember to actually draw the lines directly on the graph itself, particularly when the question asks you to use the graph to calculate the acceleration.
Area Under a Velocity-Time Graph
Higher Tier Only
The distance travelled by an object can be found by determining the area beneath a velocity-time graph
Calculating the Area Under a Velocity-Time Graph
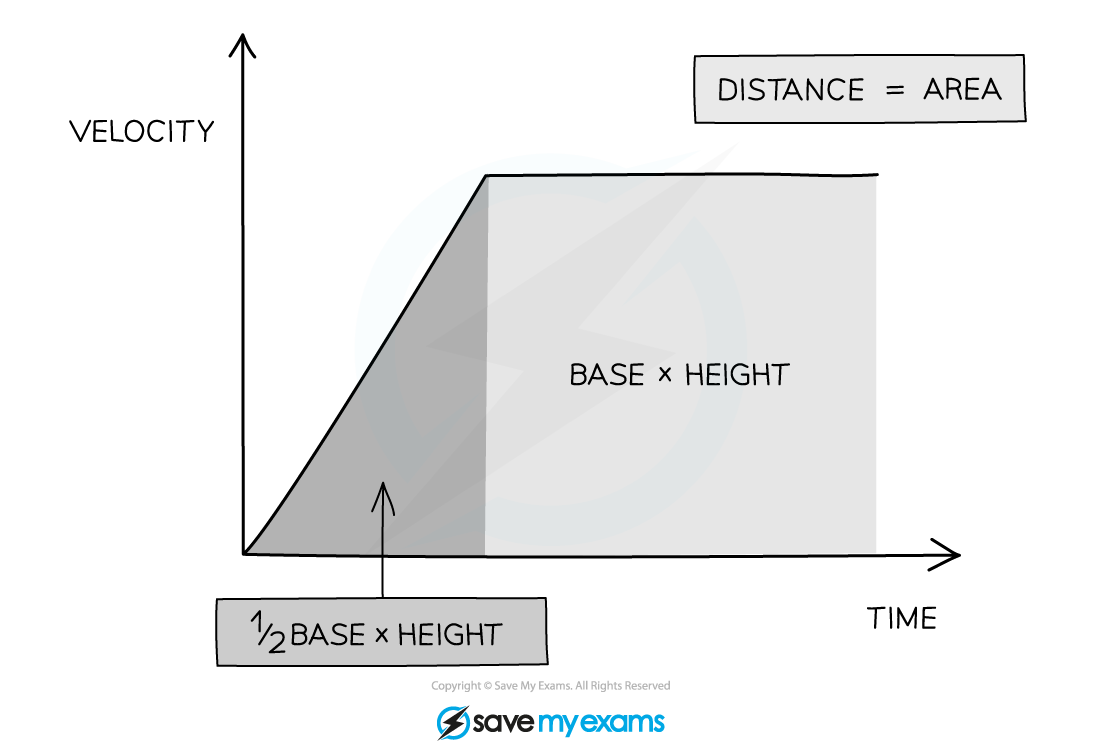
The distance travelled can be found from the area beneath the graph
If the area beneath the graph forms a triangle (the object is accelerating or decelerating) then the area can be determined using the formula:
If the area beneath the graph is a rectangle (constant velocity) then the area can be determined using the formula:
Worked Example
The velocity-time graph below shows a car journey which lasts for 160 seconds.

Calculate the total distance travelled by the car on this journey.
Answer:
Step 1: Recall that the area under a velocity-time graph represents the distance travelled
To calculate the total distance travelled, the total area underneath the line must be determined
Step 2: Identify each enclosed area
In this example, there are five enclosed areas under the line
These can be labelled as areas 1, 2, 3, 4 and 5, as shown in the image below:
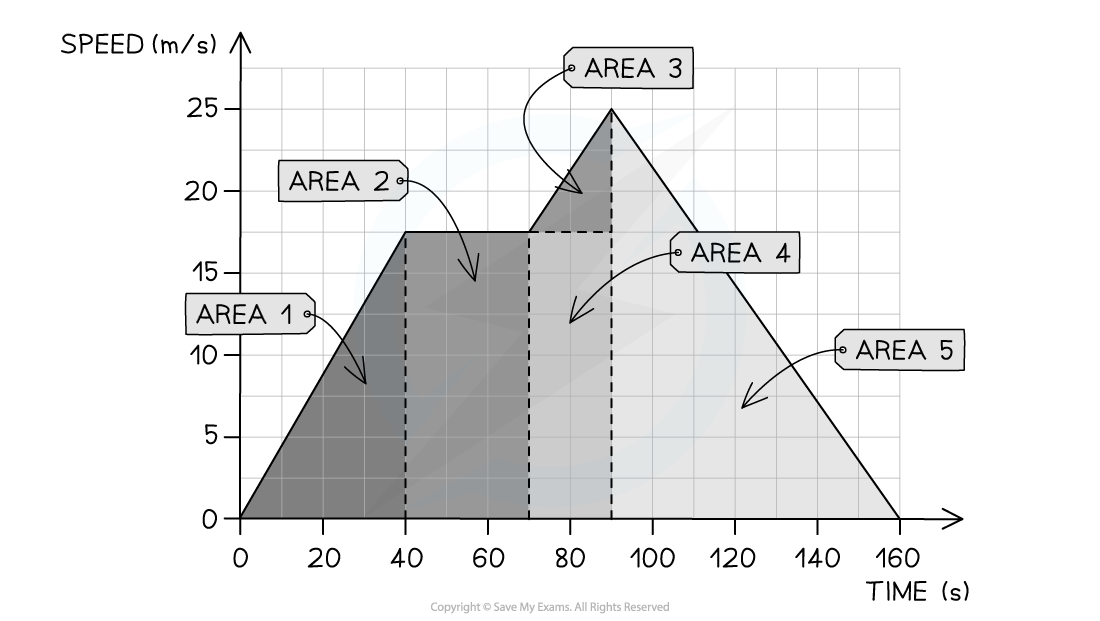
Step 3: Calculate the area of each enclosed shape under the line
Area 1 = area of a triangle = ½ × base × height = ½ × 40 × 17.5 = 350 m
Area 2 = area of a rectangle = base × height = 30 × 17.5 = 525 m
Area 3 = area of a triangle = ½ × base × height = ½ × 20 × 7.5 = 75 m
Area 4 = area of a rectangle = base × height = 20 × 17.5 = 350 m
Area 5 = area of a triangle = ½ × base × height = ½ × 70 × 25 = 875 m
Step 4: Calculate the total distance travelled by finding the total area under the line
Add up each of the five areas enclosed:
total distance = 350 + 525 + 75 + 350 + 875
total distance = 2175 m

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
