Revision NotesPast Papers
GCSEScienceWJECScience (Double Award)PhysicsRevision NotesElectricity, Energy & WavesElectric CircuitsResistors in Series & Parallel Circuits

Resistors in Series & Parallel Circuits (WJEC GCSE Science (Double Award)): Revision Note

Leander Oates

Last updated

WJEC Science (Double Award): PhysicsWJEC Physics

Resistors in Series & Parallel Circuits

  • Adding resistors in series increases the total resistance of the circuit

    • This is because in a series circuit, there is only one loop and therefore one path that the electrons can take

    • All the electrons have to pass through all the resistors, reducing the current

    • Therefore total resistance is increased

  • Adding resistors in parallel decreases the total resistance of the circuit 

    • This is because in a parallel circuit, there are multiple loops and therefore multiple paths that the electrons can take

    • These extra pathways increase the number of electrons flowing around the circuit, increasing the current

    • Therefore, total resistance is decreased

  • These rules are also true for any components (because all components have resistance)

 

How Adding Resistors in Series & Parallel affects Total Resistance

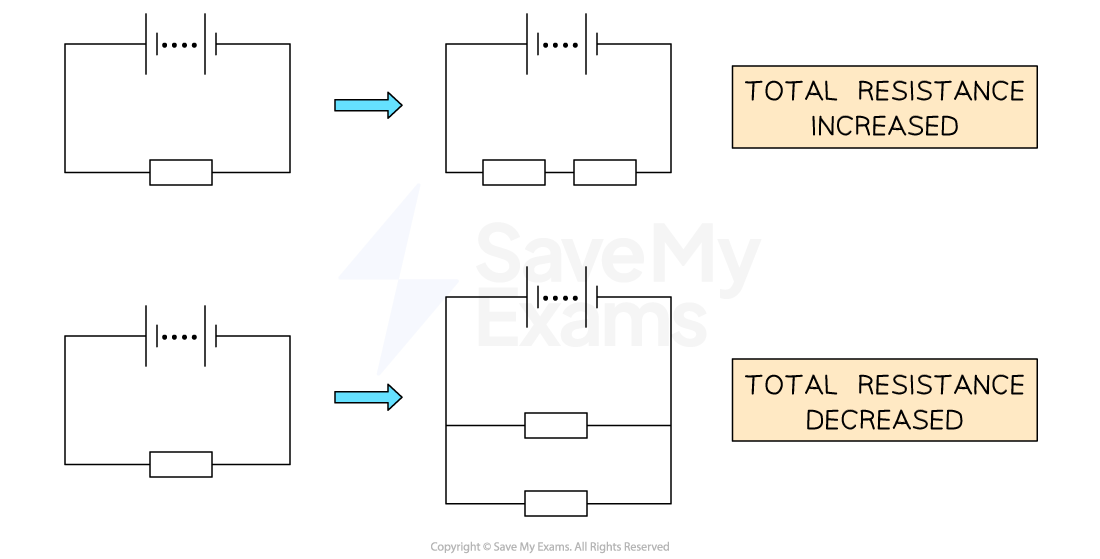
1-1-adding-resistors-in-series-and-parallel

Adding resistors in series increases the total resistance of a circuit. Adding resistors in parallel decreases the total resistance of a circuit

Calculating Resistance in Series Circuits

  • When two or more resistors are connected in series, the total resistance is equal to the sum of their individual resistances

  • For two or more resistors of resistance the total resistance can be calculated using:

R space equals space R subscript 1 space plus space R subscript 2...

  • Where:

    • R is the total resistance, in ohms (Ω)

    • R1 is the resistance of the first resistor, in ohms (Ω)

    • R2 is the resistance of the second resistor, in ohms (Ω)

  • Increasing the number of resistors in series increases the overall resistance and decreases the current

    • This is because the electrons now have more resistors to pass through

Resistance and Voltage of Resistors in Series

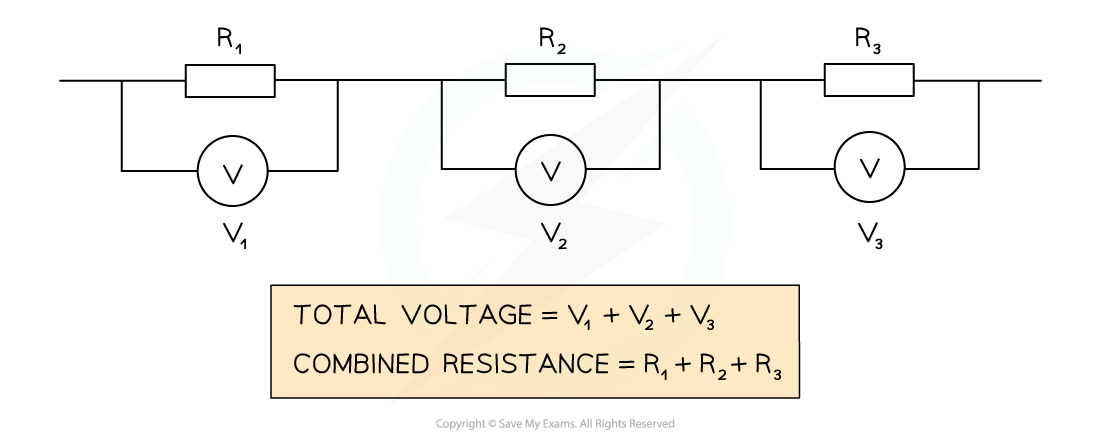
combined-resistance, IGCSE & GCSE Physics revision notes

The total resistance of resistors in series is the sum of the individual resistors. The total voltage across the resistors is the sum of the voltages across each individual resistor

Worked Example

The combined resistance R in the following series circuit is 60 Ω.What is the resistance value of R2?

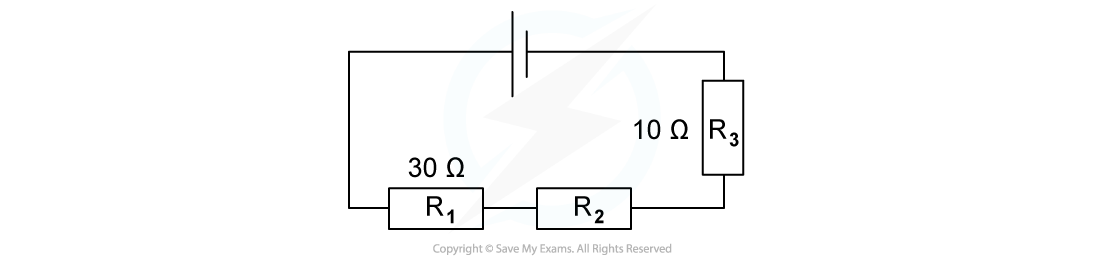
A. 100 Ω               

B. 30 Ω               

C. 20 Ω               

D. 40 Ω

Answer: C

Step 1: Write down the equation for the combined resistance in series

R = R1 + R2 + R3

Step 2: Substitute the values for total resistance R and the other resistors

60 Ω = 30 Ω + R2 + 10 Ω

Step 3: Rearrange for R2

R2 = 60 Ω – 30 Ω – 10 Ω

R2 = 20 Ω

Calculating Resistance in Parallel Circuits

Higher Tier Only

  • When two or more resistors are connected in parallel, the combined resistance decreases

  • For two or more resistors connected in parallel, the total resistance can be found by using:

1 over R space equals space 1 over R subscript 1 space plus space 1 over R subscript 2 space plus space 1 over R subscript 3...

  • Where R is the total resistance measured in ohms (Ω)

Resistors Positioned in Parallel

resistors-parallel-igcse-and-gcse-physics-revision-notes

When resistors are connected in parallel, the total resistance of the circuit is decreased

  • The advantages of resistors positioned in parallel are:

    • The components can be individually controlled, using their own switches

    • If one component stops working the others will continue to function

Worked Example

A 30 Ω resistor and a 20 Ω resistor are placed in parallel within a circuit. 

Calculate the combined resistance of these resistors.

Answer:

Step 1: Write out the equation for resistors in parallel

1 over R space equals space 1 over R subscript 1 plus 1 over R subscript 2

Step 2: Substitute in the values of the resistors

1 over R space equals space 1 over 30 space plus space 1 over 20

  • Because the values are added, it doesn't matter which resistor is R1 or R2 

Step 3: Calculate bold 1 over bold italic R

1 over R space equals space 1 over 12

  • You can use the fraction button on your calculator to type in the values, or you could do (1 ÷ 30) + (1 ÷ 20)

Step 4: Calculate R

R space equals space 12 space straight capital omega

  • To find the reciprocal you can use the reciprocal button on your calculator labelled x to the power of negative 1 end exponent or 1 over x

Examiner Tips and Tricks

The most common error that students make is giving an answer for 1 over R and forgetting to calculate R, always double check that you have remembered to do this!

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Current & Voltage RelationshipsNext:Electrical Power
    Leander Oates

    Author: Leander Oates

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.