Work Done on a Spring (OCR GCSE Combined Science A (Gateway)): Revision Note

Work Done on a Spring

• When a spring is stretched or compressed by a force, work is done by the spring

• Work done is the transfer of energy

  • The energy is transferred to its elastic potential energy store

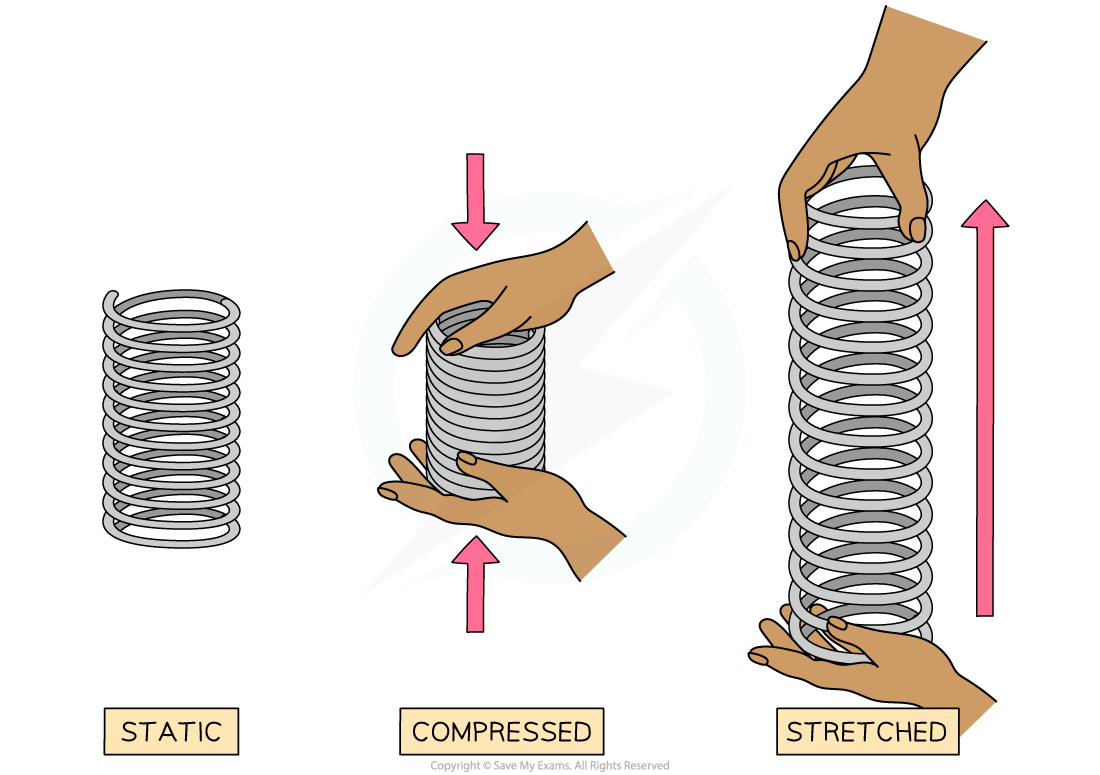
When a spring is stretched or compressed, there is work done and elastic potential energy is stored

• Elastic potential energy is defined as:

  The energy stored in an elastic object when work is done on the object

• Provided the spring is not inelastically deformed (i.e has not exceeded its limit of proportionality), the work done on the spring and its elastic potential energy stored are equal

Calculating the Work Done on a Spring

• The work done, or the elastic potential energy stored, while stretching or compressing a spring can be calculated using the equation:

E_e = ½ × k × e²

• Where:

  • E_e = elastic potential energy in joules (J)

  • k = spring constant in newtons per metre (N/m)

  • e = extension in metres (m)

The elastic potential energy in a stretched spring depends on its spring constant and extension

• This equation is only for springs that have not been stretched beyond their limit of proportionality

  • The term e² means that if the extension is doubled then the work done is quadrupled

  • This is because 2² = 4