Calculating Half-Life

Aside from calculating the half-life of an isotope, calculations involving half-life might involve
- Predicting the amount remaining, or activity, of a sample after a certain time
- Calculating the age of a sample

$100 % \overset{1 half - life}{\to} 50 % \overset{2 half - lives}{\to} 25 % \overset{3 half - lives}{\to} 12.5 %$

Half-life can also be represented in a table
As the number of half-lives increases, the proportion of the isotope remaining halves

Number of half-lives	Proportion of isotope remaining
0	1
1	$\frac{1}{2}$
2	$\frac{1}{4}$
3	$\frac{1}{8}$
4	$\frac{1}{16}$

Carbon-14 can be used to estimate the age of organic samples in a process called carbon dating
This is done by measuring the proportion of carbon-14 to the proportion of the stable isotope carbon-12
- The proportion of carbon-14 is constant in living organisms as carbon is continuously replaced during the period they are alive
- When an organism dies, the activity of the carbon-14 begins to fall
- So, the amount of carbon-14 remaining in a sample can be compared to the amount a living tissue contains to determine the approximate age of the sample

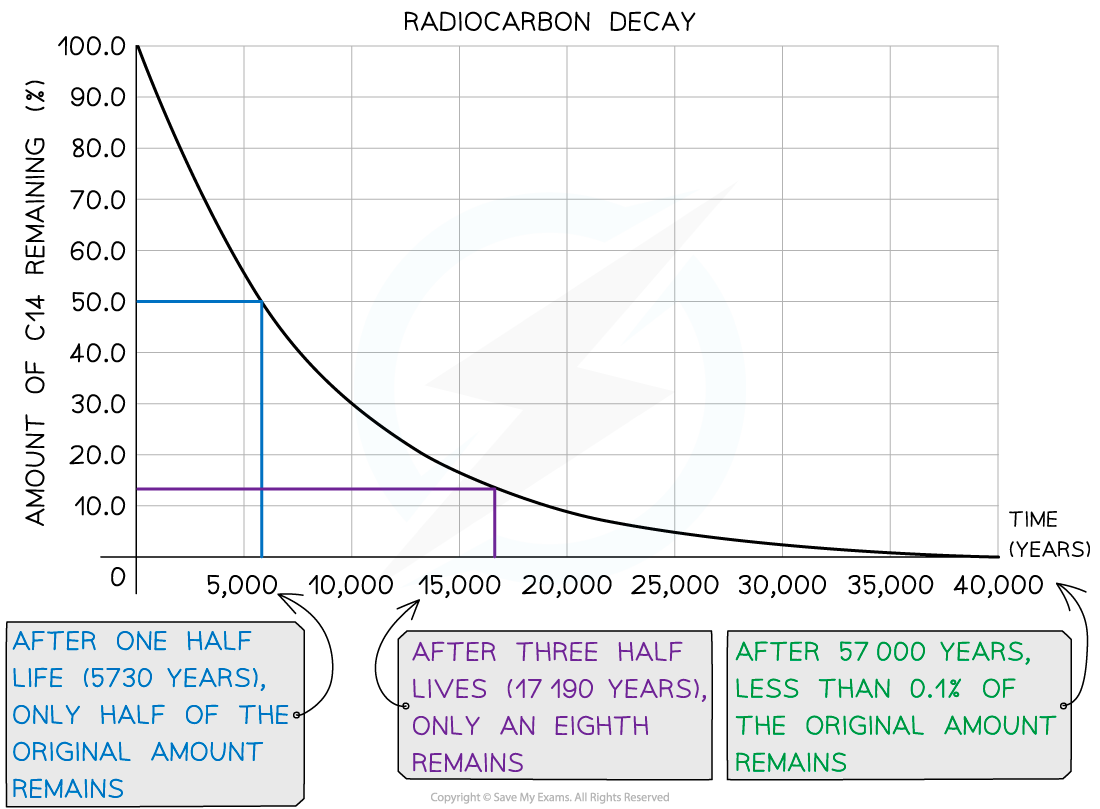
Carbon-14 has a half-life of around 5700 years
- After 5700 years, there would be 50% of the original amount of carbon-14 remaining
- After two half-lives, or 11 400 years, there would be just 25% of the carbon-14 remaining

Radiocarbon Decay

A particular radioactive sample contains 2 million undecayed atoms. After a year, there are 500 000 atoms left undecayed.

Calculate the half-life of this sample.

Answer:

Step 1: Calculate how many times the number of un-decayed atoms has halved

Step 2: Divide the time period by the number of half-lives

$1 year \overset{1 half life}{\to} 6 months \overset{2 half lives}{\to} 3 months$

Carbon-14 has a half-life of 5730 years. A sample of ancient wood is found to have 12.5% of the carbon-14 as a living sample.

Estimate the age of the sample of ancient wood.

Answer:

Step 1: Determine the number of half-lives that have passed

$100 % \overset{1 half - life}{\to} 50 % \overset{2 half - lives}{\to} 25 % \overset{3 half - lives}{\to} 12.5 %$

Step 2: Determine the age of the sample

age = 3 × 5730 = 17 190 years old

Calculating Half-Life (WJEC GCSE Physics: Combined Science)