GCSEPhysics: Combined ScienceWJECRevision NotesForces, Space & RadioactivityDistance, Speed & AccelerationThinking, Braking & Stopping Distances

Thinking, Braking & Stopping Distances (WJEC GCSE Physics: Combined Science)

Revision Note

Ann H

Author

Ann H

Last updated

Thinking, Braking & Stopping Distances

Principles of Forces and Motion

  • When a driver applies the brakes, there is a frictional force between the brakes and the wheels of the car, also known as the braking force
  • This frictional force does work on the brakes - i.e. it transfers energy from the car to the brakes
  • Therefore, the kinetic energy of the car decreases and the thermal energy of the brakes increases - i.e. the brakes heat up
  • This means the car decelerates (slows down)

Work Done when the Braking Force is Applied

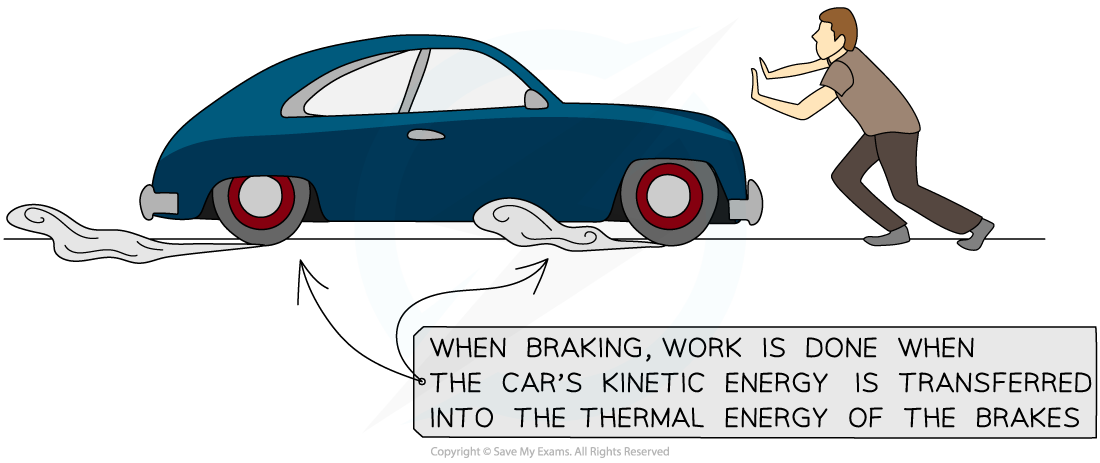
Braking and Friction, downloadable IGCSE & GCSE Physics revision notes

Work done by breaking transfers energy from the kinetic store into the thermal energy store 

  • The greater the speed of a vehicle, the greater the braking force required to bring the vehicle to a halt for a given distance
    • This is due to the link between resultant force and acceleration as stated in Newton's second law of motion
    • Since the braking force would need to be larger, the deceleration of the vehicle will be large as well
  • Large decelerations could lead to the brakes overheating and / or loss of control of the vehicle

Stopping Distance

  • The stopping distance of a car is defined as:

The total distance travelled during the time it takes for a car to stop in response to some emergency

  • It can be written as an equation involving two distances:

Stopping distance = Thinking distance + Braking distance

Thinking Distance

  • Thinking distance is defined as

The distance travelled in the time it takes the driver to react (reaction time) in metres (m)

  • The main factors affecting thinking distance are:
    • The speed of the car
    • The reaction time of the driver 
  • The reaction time is defined as:

A measure of how much time passes between seeing something and reacting to it

  • The average reaction time of a human is 0.25 s
  • Reaction time is increased by:
    • Tiredness
    • Distractions (e.g. using a mobile phone)
    • Intoxication (i.e. consumption of alcohol or drugs)

Breaking Distance

  • Braking distance is defined as

the distance travelled under the braking force in metres (m)

  • For a given braking force, the greater the speed of the vehicle, the greater the stopping distance

Calculating Stopping Distance

  • For a given braking force, the speed of a vehicle determines the size of the stopping distance
  • The greater the speed of the vehicle, the larger the stopping distance

The Effect of Speed on Stopping Distance

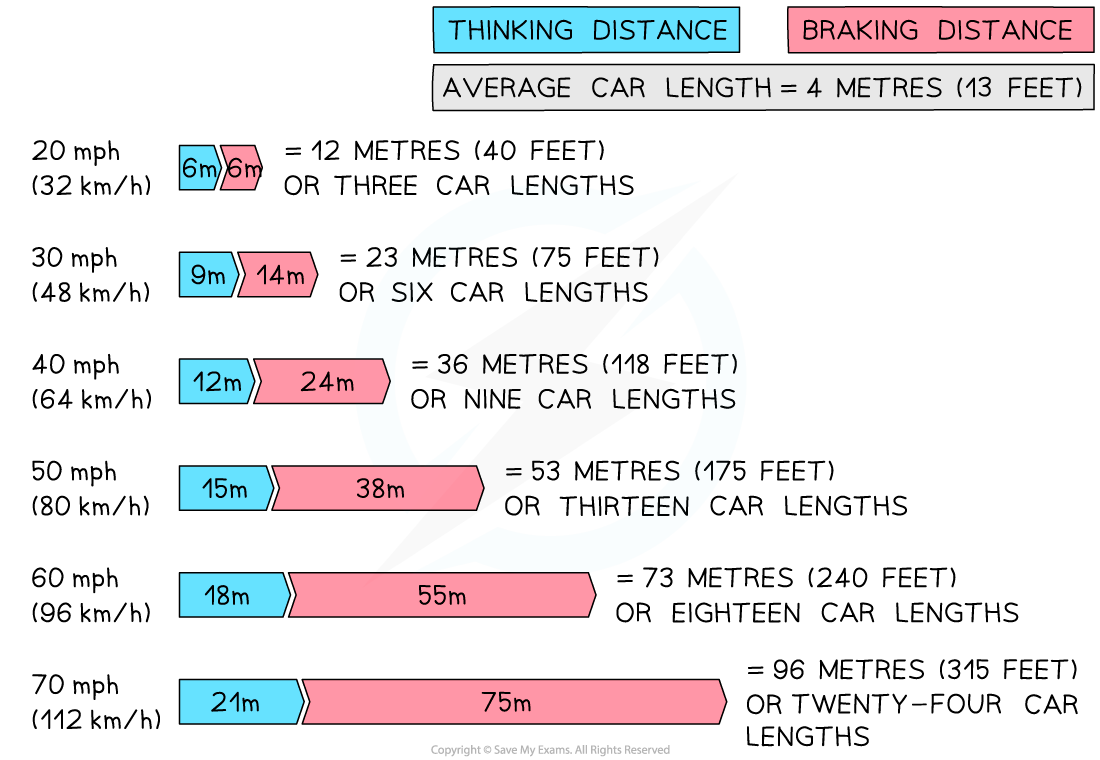
Highway Code, downloadable IGCSE & GCSE Physics revision notes

A vehicle's stopping distance increases with speed. At a speed of 20 mph the stopping distance is 12 m, whereas at 60 mph the stopping distance is 73 m (reproduced from the UK Highway Code) 

A Table Showing Speed and Stopping Distance

Speed (mph) Speed (m/s) Stopping Distances (m)
20 9 12
30 14 23
40 18 36
50 22 53
60 27 73

Worked example

At a speed of 20 m/s, a particular vehicle had a stopping distance of 40 metres. The car travelled 14 metres whilst the driver was reacting to the incident in front of him.

What was the braking distance?

A      54 m

B      34 m

C      26 m

D      6 m

Answer:  C

Step 1: Identify the different variables

  • Stopping distance = 40 m
  • Thinking distance = 14 m

Step 2: Rearrange the formula for stopping distance

Stopping distance = Thinking distance + Braking distance

Braking distance = Stopping distance – Thinking distance

Step 3: Calculate and identify the correct braking distance

Braking distance = 40 – 14

Breaking distance = 26 metres

Therefore, the answer is C

Worked example

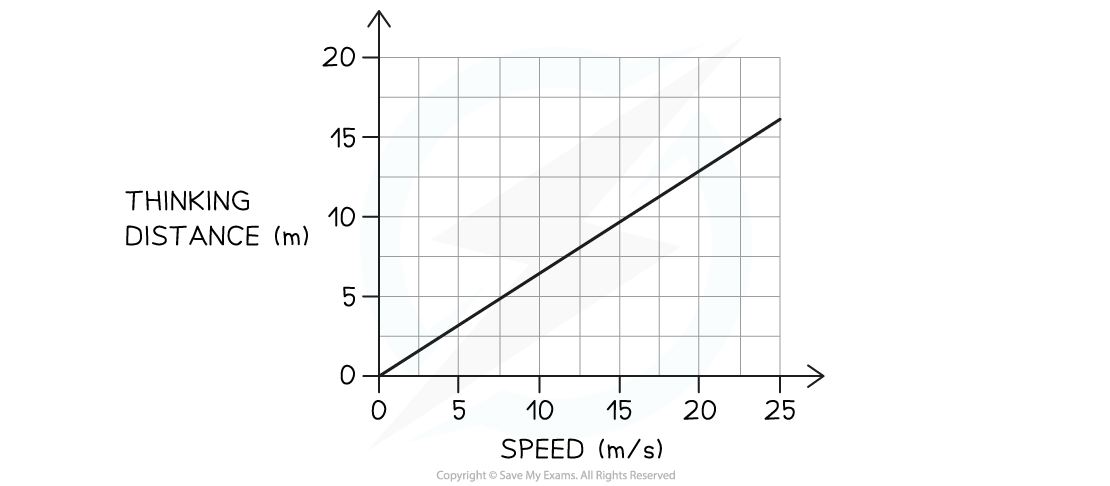
The graph below shows how the thinking distance of a driver depends on the speed of the car.WE Thinking distance question graph, downloadable IGCSE & GCSE Physics revision notes

(a)
Use the graph to describe the relationship between thinking distance and speed.
 
(b)
Some people drive when they are tired, despite warnings against doing so.
Draw a new line on the graph to show how thinking distance varies with speed for a tired driver.

Answer:

Part (a)

Step 1: Check if the line is straight and if it goes through the origin

  • The graph shows a straight line through the origin
  • Therefore, the thinking distance is directly proportional to the speed of the car

Part (b)

Step 1: Recall the factors which affect the thinking distance

  • Three additional factors affect the thinking distance, because they affect human reaction time:
    • Tiredness
    • Distractions
    • Intoxication
  • Hence, a tired driver's reaction time is greater (i.e. it takes longer for them to react)

Step 2: Draw a line that shows greater thinking distance for the same speed

  • At the same speed, a tired driver's thinking distance will be greater than a driver who is alert
  • This means a line should be drawn with a steeper gradient, as shown below:

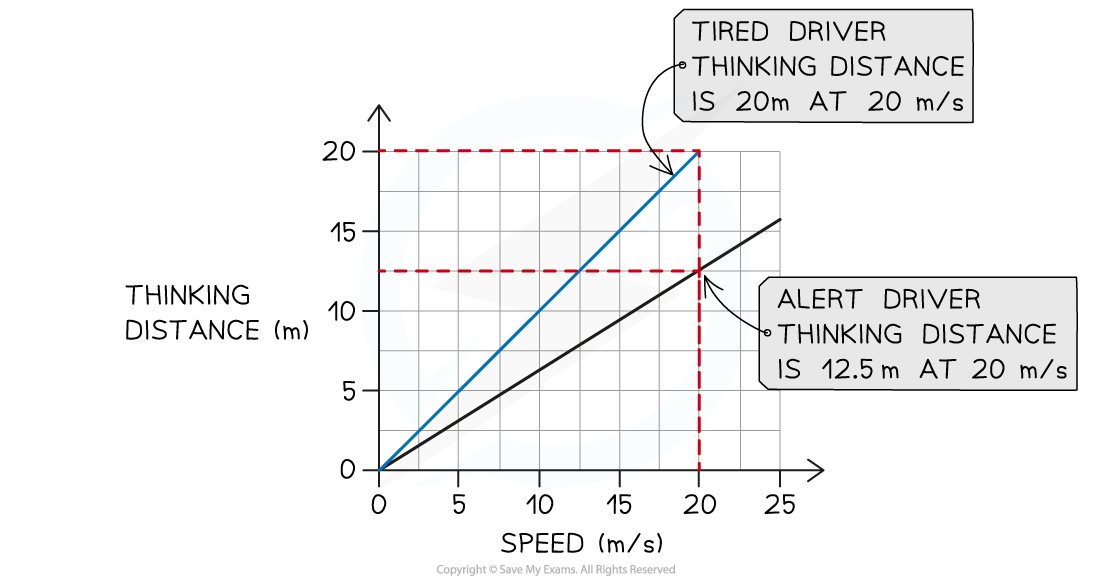
WE Thinking distance solution graph, downloadable IGCSE & GCSE Physics revision notes

Worked example

Higher Tier

A car is travelling at 15 m/s when the driver applies the brakes. The car decelerates uniformly and stops. The mass of the car and the driver is 1500 kg, and together they have a total kinetic energy of 168 750 J.

(a)
Determine the work done by the braking force to stop the car and the driver.
 
(b)
The braking force used to stop the car and the driver was 6000 N.
Calculate the braking distance of the car.

Answer:

Part (a)

Step 1: Recall the process of applying brakes to a vehicle

  • The work done is the energy transferred from the car and driver to the brakes
  • This energy transfer is from kinetic energy to thermal energy
  • In this case, the car is brought to a complete stop, so 168 750 J of energy is transferred from kinetic energy to heating up the brakes (assuming all energy is transferred to heat only!)

Part (b)

Step 1: State the equation for work done

Work done = Force × distance travelled

W space equals space F s

  • In this case, the force doing the work (transferring energy) is the braking force

Step 2: Rearrange the equation and solve for distance travelled

s space equals fraction numerator space W over denominator F end fraction

Step 3: Substitute the values for work and force 

s space equals fraction numerator space 168 space 750 over denominator 6000 end fraction

s space equals space 28.1 space straight m

  • Hence the braking distance (the distance travelled by the car under the braking force) is 28.1 m

Examiner Tip

If you are asked to explain why the temperature of the brakes increases when a vehicle stops, remember, work is done by the frictional force between the brakes and the wheel. It's a common mistake to write about the friction between the wheels and the road. This does happen, but in this case, the wheels heat up the road! The brake temperature increases because there is a transfer of energy from the car's kinetic energy to the thermal energy of the brakes.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Velocity-Time GraphsNext:Traffic Control Measures
    Ann H

    Author: Ann H

    Expertise: Physics

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students no matter their schooling or background.