Calculating Radioactive Decay (OCR Gateway GCSE Physics: Combined Science)

• To calculate the half-life of a sample, the procedure is:
  • Measure the initial activity, A₀, of the sample
  • Determine the half-life of this original activity
  • Measure how the activity changes with time

• The time taken for the activity to decrease to half its original value is the half-life
• Half-life can be shown clearly on a graph

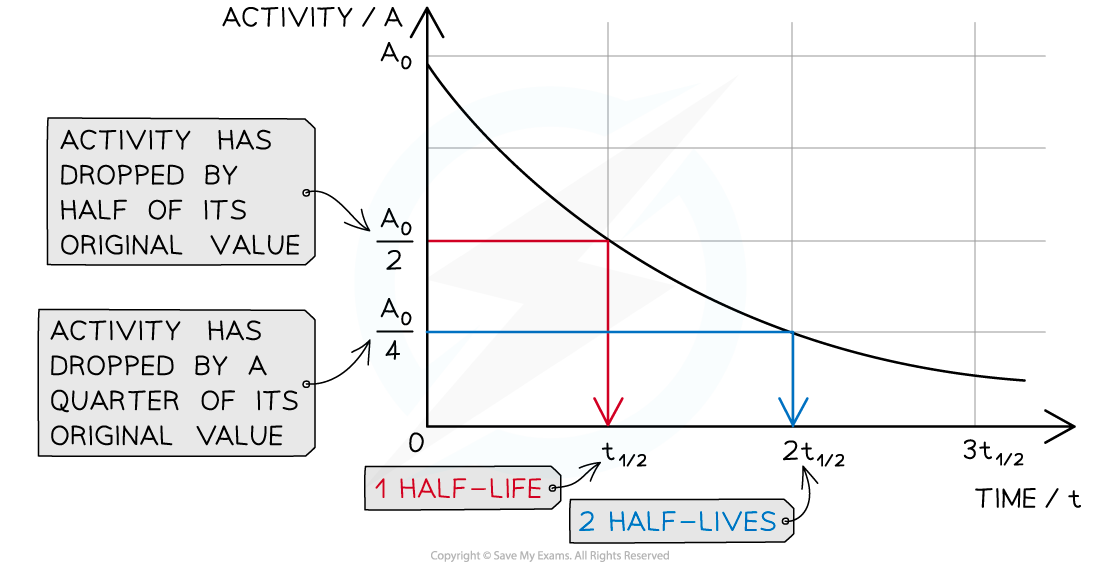
The diagram shows how the activity of a radioactive sample changes over time. Each time the original activity halves, another half-life has passed

• The time it takes for the activity of the sample to decrease from 100 % to 50 % is the half-life
• It is the same length of time as it would take to decrease from 50 % activity to 25 % activity
• The half-life is constant for a particular isotope

Step 1: Draw lines on the graph to determine the time it takes for technetium to drop to half of its original activity

Step 2: Read the half-life from the graph

• • In the diagram above the initial activity, A₀, is 8 × 10⁷ Bq
  • The time taken to decrease to 4 × 10⁷ Bq, or ½ A₀, is 6 hours
  • The time taken to decrease to 2 × 10⁷ Bq is 6 more hours
  • The time taken to decrease to 1 × 10⁷ Bq is 6 more hours
  • Therefore, the half-life of this isotope is 6 hours

Step 1: Calculate how many times the number of un-decayed atoms has halved

• • There were 2 000 000 atoms to start with
  • 1 000 000 atoms would remain after 1 half-life
  • 500 000 atoms would remain after 2 half-lives
  • Therefore, the sample has undergone 2 half-lives

Step 2: Divide the time period by the number of half-lives

• • The time period is a year
  • The number of half-lives is 2

• • 1 year divided by 4 (2²) is a quarter of a year or 3 months
  • Therefore, the half-life of the sample is 3 months