Specific Heat Capacity (AQA GCSE Physics: Combined Science)

• If the temperature of the system increases, the increase in temperature of this system depends on:
  • The mass of the substance heated
  • The type of material
  • The energy input to the system

• Energy is transferred to the thermal store of the substance 
• The amount of energy needed to raise the temperature of a given mass by a given amount can be calculated using the equation:

ΔE = mcΔθ

• Where:
  • ΔE = change in energy, in joules (J)
  • m = mass, in kilograms (kg)
  • c = specific heat capacity, in joules per kilogram per degree Celsius (J/kg °C)
  • Δθ = change in temperature, in degrees Celsius (°C)

• The specific heat capacity, c of a substance is defined as:

The amount of energy required to raise the temperature of 1 kg of the substance by 1 °C

• Different substances have different specific heat capacities

• If a substance has a low specific heat capacity, it heats up and cools down quickly
  • It takes less energy to change its temperature
• If a substance has a high specific heat capacity, it heats up and cools down slowly
  • It takes more energy to change its temperature 

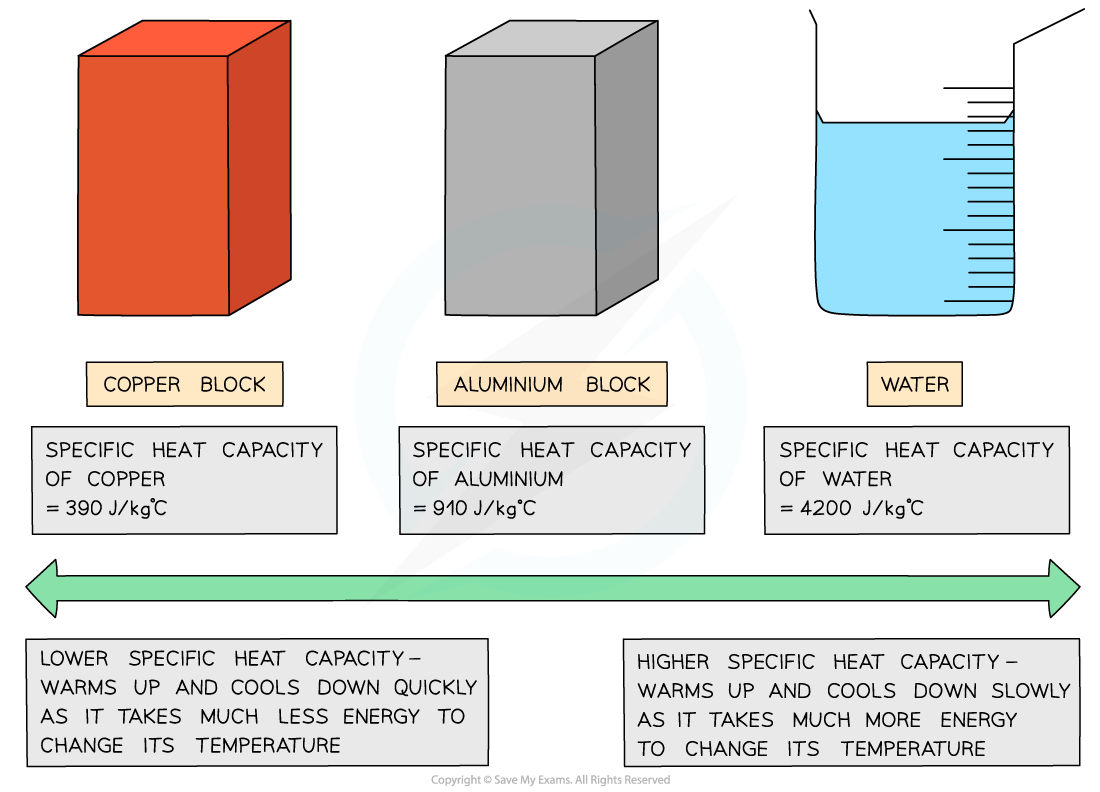
Low v high specific heat capacity

• Specific heat capacity is mainly used for liquids and solids
• The specific heat capacity of different substances determines how useful they would be for a specific purpose eg. choosing the best material for kitchen appliances
  • Good electrical conductors, such as copper and lead, are excellent conductors of heat due to their low specific heat capacity
  • On the other hand, water has a very high specific heat capacity, making it ideal for heating homes as the water remains hot in a radiator for a long time

• The specific heat capacity of some substances are given in the table below as examples:

Table of values of specific heat capacity for various substances

Step 1: Write down the known quantities

• • Mass, m = 0.48 kg
  • Change in temperature, Δθ = 0.7 °C
  • Specific heat capacity, c = 4200 J / kg °C

Step 2: Write down the relevant equation 

ΔE = mcΔθ

Step 3: Calculate the energy transferred by substituting in the values

ΔE = (0.48) × (4200) × (0.7) = 1411.2

Step 4: Round the answer to 2 significant figures

ΔE = 1400 J