Nuclear Equations for Fission & Fusion (WJEC GCSE Physics)

Revision Note

Author

Katie M

Last updated

29 February 2024

Balancing Nuclear Equations for Fission & Fusion

Nuclear Fission Equations

An example of a fission reaction is uranium-235 being bombarded with a neutron to produce two daughter nuclei, three neutrons and energy in the form of gamma radiation
This can be written in the form of an equation:

${}_{92}^{235}U + {}_{0}^{1}n \to {}_{36}^{92}{Kr} + {}_{56}^{141}{Ba} + 3 {}_{0}^{1}n$ + energy

Where:
- ${}_{92}^{235}U$ is an isotope of uranium
- ${}_{0}^{1}n$ is a neutron
- ${}_{36}^{92}{Kr}$ is an isotope of krypton (one daughter nucleus)
- ${}_{56}^{141}{Ba}$ is an isotope of barium (the other daughter nucleus)

The sum of the top (nucleon) numbers on the left-hand side equals the sum of the top number on the right-hand side: 235 + 1 = 92 + 141 + (3 × 1)
The same is true for the lower (proton) numbers: 92 + 0 = 36 + 56 + (3 × 0)

Representing Nuclear Fission Reactions

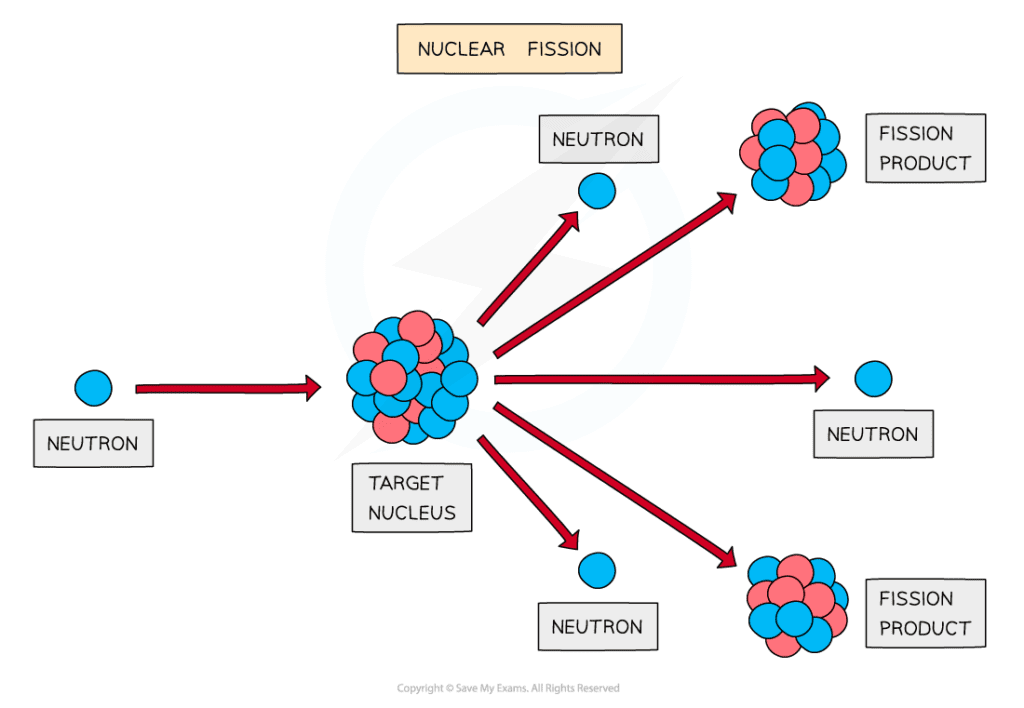
Nuclear fission

A neutron is fired at a target nucleus, causing it to split into two fission products plus 3 neutrons

The above equation represents a fission reaction where
- A uranium nucleus absorbs a neutron
- It splits into two smaller nuclei – a krypton nucleus and a barium nucleus
- Three neutrons are released in the process, along with a large amount of energy

Nuclear Fusion Equations

An example of a fusion reaction is deuterium and tritium nuclei combining at high energies to produce a helium nucleus, a neutron and a lot of energy
This can be written as a nuclear equation:

${}_{1}^{2}H + {}_{1}^{3}H \to {}_{2}^{4}{He} + {}_{0}^{1}n$ + energy

Where:
- ${}_{1}^{2}H$ is deuterium (an isotope of hydrogen with 1 proton and 1 neutron)
- ${}_{1}^{3}H$ is tritium (an isotope of hydrogen with 1 proton and 2 neutrons)
- ${}_{2}^{4}{He}$ is a stable helium nucleus
- ${}_{0}^{1}n$ is a neutron

The sum of the top (nucleon) numbers on the left-hand side equals the sum of the top number on the right-hand side: 2 + 3 = 4 + 1
The same is true for the lower (proton) numbers: 1 + 1 = 2 + 0

Representing Nuclear Fusion Reactions

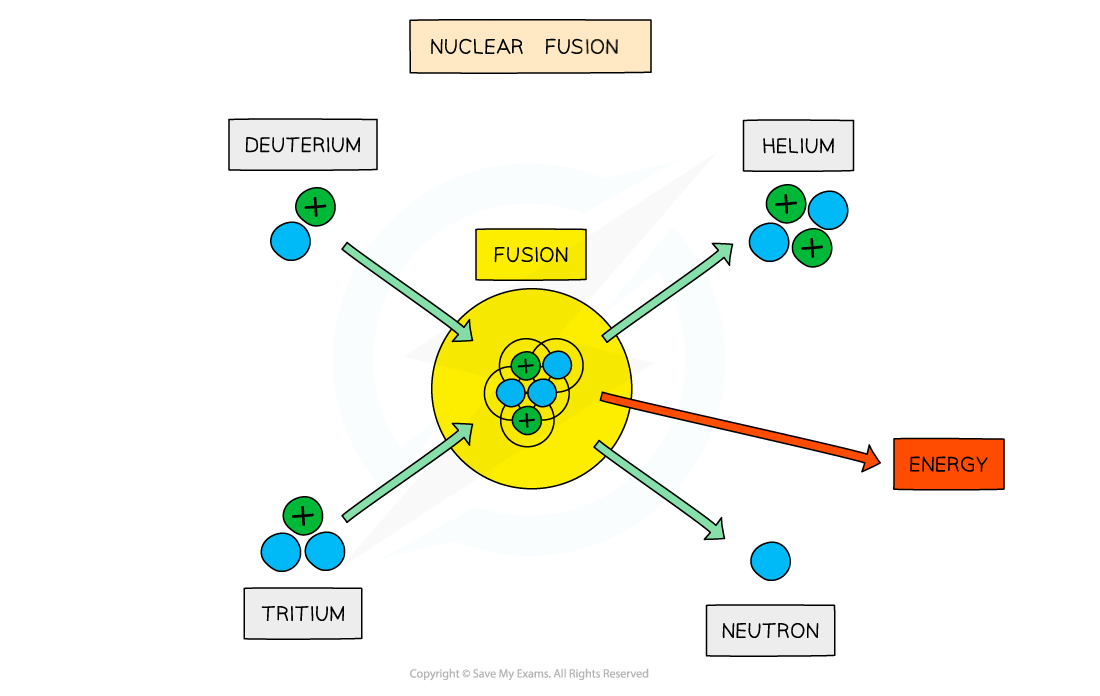
Nuclear Fusion

Isotopes of hydrogen, deuterium and tritium, can fuse into a helium nucleus and a neutron plus the release of energy

The above equation represents a fusion reaction where
- A deuterium nucleus collides with a tritium nucleus
- They become close enough to fuse into a helium-4 nucleus
- A neutron is released in the process, along with a large amount of energy

Worked example

A possible nuclear equation for the fission of uranium-235 is

${}_{92}^{235}U + {}_{0}^{1}n \to {}_{37}^{96}{Rb} + {}_{55}^{137}{Cs} + N {}_{0}^{1}n$

Calculate the number of neutrons N released in this reaction.

Answer:

Step 1: Calculate the nucleon number on the left side of the equation

235 + 1 = 236

Step 2: Calculate the nucleon number on the right side of the equation

96 + 138 + (N × 1) = 233 + N

Step 3: Equate the nucleon number for both sides of the equation

236 = 233 + N

Step 4: Rearrange for the number of neutrons, N

N = 236 – 233 = 3

Worked example

One of the nuclear fusion reactions that occurs in the Sun is shown below.

${}_{. . . . .}^{. . . . .}H + {}_{. . . . .}^{. . . . .}H \to {}_{2}^{3}{He} + γ$

Complete the equation.

Answer:

Step 1: Recall the proton number for hydrogen and the meaning of isotope

Isotopes are elements with the same proton number but different nucleon numbers
Hydrogen has a proton number of 1
So, the bottom number for both hydrogen nuclei is 1

Step 2: Determine the nucleon numbers of the hydrogen isotopes

The total nucleon number on the right side of the equation is 3, as gamma is an electromagnetic wave so does not have a nucleon or proton number
The hydrogen nuclei on the left side are isotopes
Therefore, their nucleon numbers must be 1 and 2

Step 3: Write the equation out in full and check both sides

${}_{1}^{1}H + {}_{1}^{2}H \to {}_{2}^{3}{He} + γ$

Nucleon numbers: 1 + 2 = 3 + 0
Proton numbers: 1 + 1 = 2 + 0
The numbers balance, so the equation must be correct

Writing Nuclear Equations for Fission & Fusion

Higher Tier

Given some information about different nuclei, you could be asked to write full, balanced nuclear equations for particular nuclear reactions, such as fission or fusion
Remember the key rule for writing balanced equations:

The sum of the nucleon numbers and proton numbers must be equal before and after the reaction

In nuclear fusion equations:
- Two small nuclei react
- One larger nucleus is produced
- There may be a neutron released, but not always

In nuclear fission equations:
- One large nucleus absorbs a neutron
- Two smaller nuclei are produced
- Two or three neutrons are always released

The worked examples below illustrate the kinds of questions that could be asked

Worked example

The diagram below shows an example of a nuclear fusion reaction in which two isotopes of helium $(He)$ fuse together to make a beryllium-7 $({}_{4}^{7}{Be})$ nucleus plus the emission of a gamma ray.

2-9-worked-example---writing-fusion-equationsworked-example---writing-fusion-equations

Write a balanced nuclear equation for this fusion reaction.

Answer:

Step 1: Write a word equation using the information in the question

Underline or highlight the keywords in the question:

"Two isotopes of helium fuse together to make a beryllium-7 nucleus plus the emission of a gamma ray"

Write a word equation for the reaction:

helium + helium → beryllium-7 + gamma

Step 2: Work out the symbols for the helium isotopes

The notation for beryllium-7 is
- This means it contains 4 protons and 3 neutrons
- Using the diagram, we can deduce the light particles are protons and the dark particles are neutrons

Isotopes are elements with the same proton number but different nucleon numbers
So, both helium nuclei must have a proton number of 2
The two helium isotopes are therefore:
- Helium-3: ${}_{2}^{3}{He}$ (2 protons, 1 neutron)
- Helium-4: ${}_{2}^{4}{He}$ (2 protons, 2 neutrons)
Gamma particles have no mass or charge so have nucleon and proton numbers of 0

Step 3: Write the balanced nuclear equation using the correct symbols

${}_{2}^{3}{He} + {}_{2}^{4}{He} \to {}_{4}^{7}{Be} + {}_{0}^{0}γ$

Nucleon numbers: 3 + 4 = 7 + 0
Proton numbers: 2 + 2 = 4 + 0
The numbers balance, so the equation must be correct

Worked example

The table shows some information about different nuclei involved in a nuclear fission reaction.

Nucleus	Symbol	Number of protons	Number of neutrons
Uranium	U	92	143
Barium	Ba	56	88
Krypton	Kr	36	53

A nucleus of uranium undergoes fission when bombarded with a slow-moving neutron (n) causing it to split into the daughter nuclei barium and krypton plus the release of further neutrons.

Write a balanced nuclear equation for this fission reaction.

$. . . . . . . . . + . . . . . . . . . \to . . . . . . . . . + . . . . . . . . . + . . . . . . . . .$

Answer:

Step 1: Write a word equation using the information in the question

Underline or highlight the keywords in the question which tell us about the nuclei on the left-hand side (LHS):

"A nucleus of uranium undergoes fission when bombarded with a slow-moving neutron"

Underline or highlight the keywords in the question which tell us about the nuclei on the right-hand side (RHS):

"causing it to split into the daughter nuclei barium and krypton plus the release of further neutrons"

Write a word equation for the reaction:

uranium + neutron → barium + krypton + neutrons

Step 2: Determine the correct symbols for each nucleus or particle

We need to write each nucleus or particle in ${}_{Z}^{A}X$ notation
It can be useful to draw an extra row and column onto the table to do this (green indicates the changes made to the table):

Nucleus	Symbol ${}_{Z}^{A}X$	Number of protons Z	Number of neutrons	Nucleon number A
Uranium	${}_{92}^{235}U$	92	143	92 + 143 = 235
Barium	${}_{56}^{144}{Ba}$	56	88	56 + 88 = 144
Krypton	${}_{36}^{89}{Kr}$	36	53	36 + 53 = 89
Neutron	${}_{0}^{1}n$	0	1	0 + 1 = 1

Step 3: Write the nuclear equation using the symbols

${}_{92}^{235}U + {}_{0}^{1}n \to {}_{56}^{144}{Ba} + {}_{36}^{89}{Kr} + {}_{0}^{1}n$

Step 4: Balance the equation by checking the total nucleon and proton numbers on each side

Total proton number:
- On the LHS: 92 + 0 = 92
- On the RHS: 56 + 36 + 0 = 92
The total proton number is the same on both sides

Total nucleon number:
- On the LHS: 235 + 1 = 236
- On the RHS: 144 + 89 + 1 = 234

There is a difference of 2, and the question states there is a "release of further neutrons"
This means there must be 2 extra neutrons released i.e. 3 neutrons in total
To represent this, we put a 3 in front of the neutron symbol on the RHS, so, the fully balanced equation is:

${}_{92}^{235}U + {}_{0}^{1}n \to {}_{56}^{144}{Ba} + {}_{36}^{89}{Kr} + 3 {}_{0}^{1}n$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Fusion

Nuclear Equations for Fission & Fusion (WJEC GCSE Physics)

Revision Note

Nuclear Fission Equations

Representing Nuclear Fission Reactions

Nuclear Fusion Equations

Representing Nuclear Fusion Reactions

Higher Tier

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M