The Principle of Moments (WJEC GCSE Physics): Revision Note
Exam code: 3420
The Principle of Moments
Forces and Rotation
Forces can cause the rotation of an object about a fixed pivot
This rotation can be clockwise or anticlockwise
Clockwise and Anti-clockwise Rotation
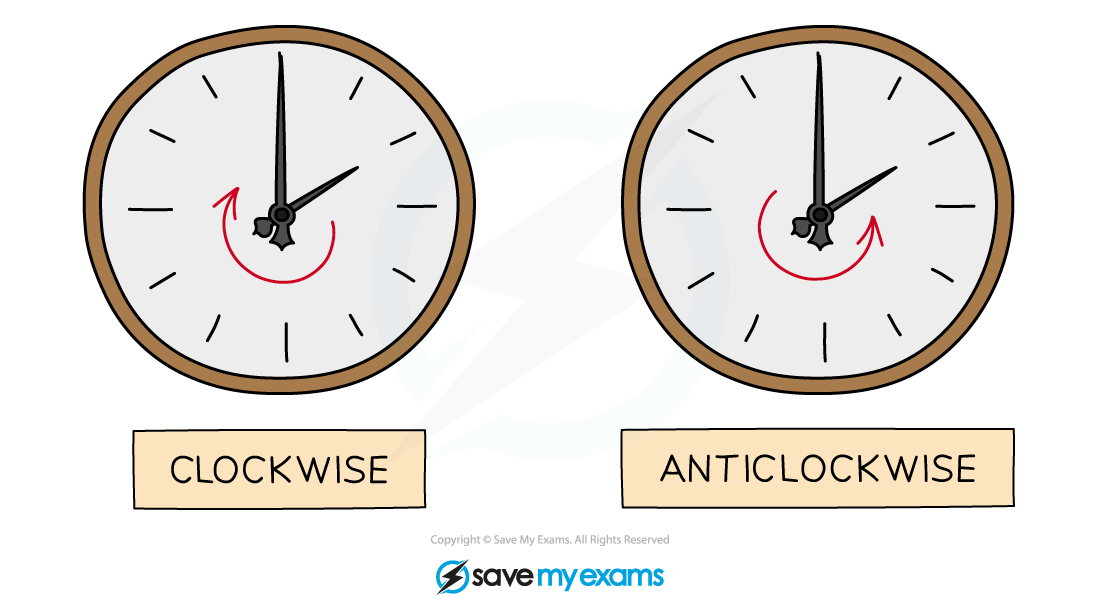
Consider the hands of a clock when deciding if an object will rotate in a clockwise or anti-clockwise direction
A force applied on one side of the pivot will cause the object to rotate
An Object Rotating Clockwise About a Pivot

The force will cause the object to rotate clockwise about the pivot
Examples of the rotation caused by a force are:
A child on a see-saw
Turning the handle of a spanner
A door opening and closing
Using a crane to move building supplies
Using a screwdriver to open a tin of paint
Turning a tap on and off
Picking up a wheelbarrow
Using scissors
Moments
A moment is defined as:
A turning force about a pivot
The size of a moment is defined by the equation:
M = F × d
Where:
M = moment in newton metres (N m)
F = force in newtons (N)
d = distance perpendicular to the direction of the force in metres (m)
The forces should be perpendicular to the distance from the pivot
For example, on a horizontal beam, the forces which will cause a moment are those directed upwards or downwards
The Moments on a Spanner
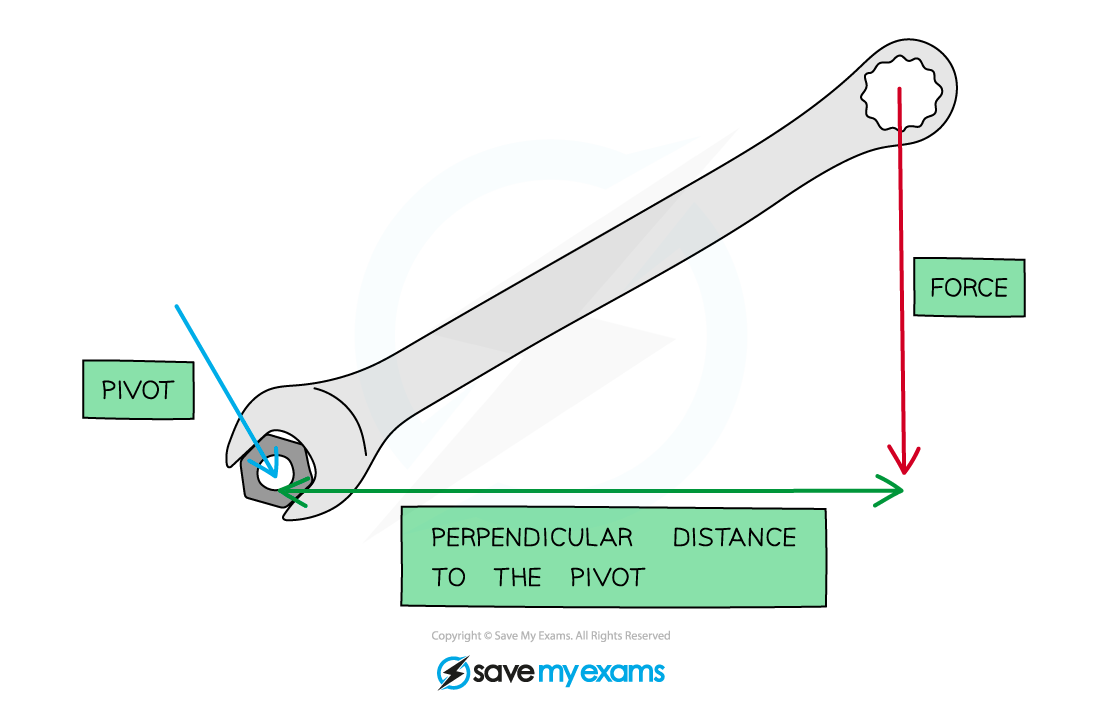
The moment depends on the force and perpendicular distance to the pivot
Increasing the distance a force is applied from a pivot decreases the force required
If you try to push open a door right next to the hinge it is very difficult, as it requires a lot of force
If you push the door open at the side furthest from the hinge then it is much easier, as less force is required
Forces Required to Open a Door

A greater force is required to push open a door next to the hinges than at the door handle
The Principle of Moments
The principle of moments states that:
For a body in equilibrium, the sum of the clockwise moments equals the sum of the anticlockwise moments about the same pivot
A body in equilibrium means the moments on both sides of the pivot are equal and balanced
Clockwise and Anticlockwise Moments
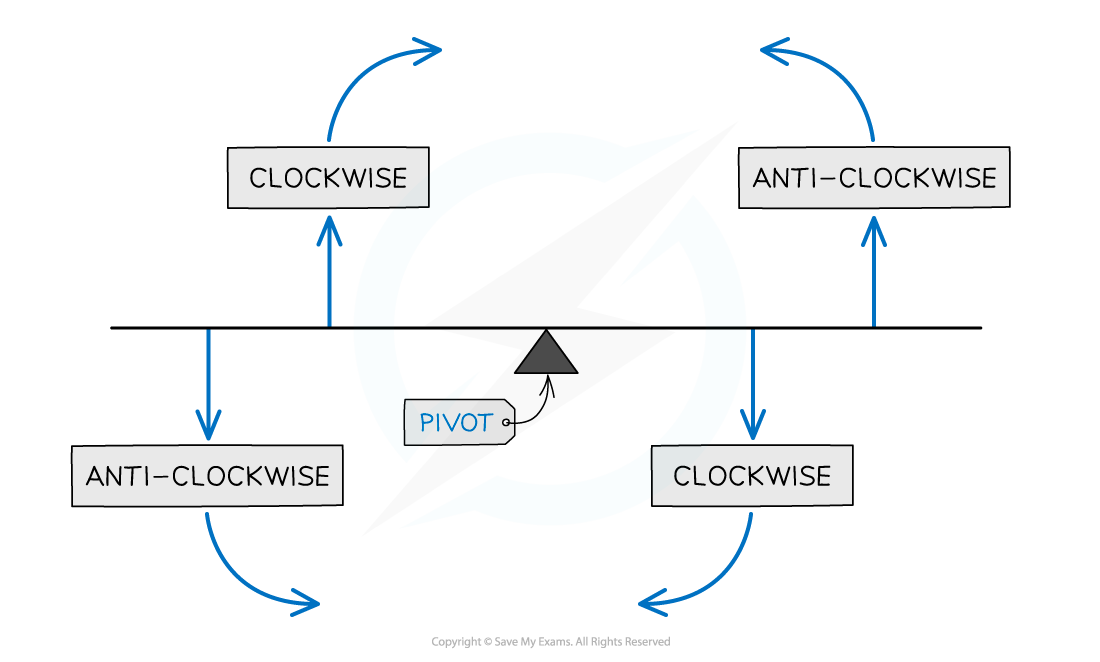
Imagine holding the beam about the pivot and applying just one of the forces. If the beam moves clockwise then the force applied is clockwise.
In the example below, the forces and distances of the objects on the beam are different, but they are arranged in a way that balances the whole system
Using the Principle of Moments

The clockwise and anticlockwise moments acting on a beam are balanced
In the above diagram:
Force
causes an anticlockwise moment of
about the pivot
Force
causes a clockwise moment of
about the pivot
Force
causes an anticlockwise moment of
about the pivot
Collecting the clockwise and anticlockwise moments:
Sum of the clockwise moments =
Sum of the anticlockwise moments =
Using the principle of moments, the beam is balanced when:
Sum of the clockwise moments = Sum of the anticlockwise moments
Worked Example
A parent and child are at opposite ends of a playground see-saw. The parent weighs 690 N and the child weighs 140 N. The adult sits 0.3 m from the pivot.
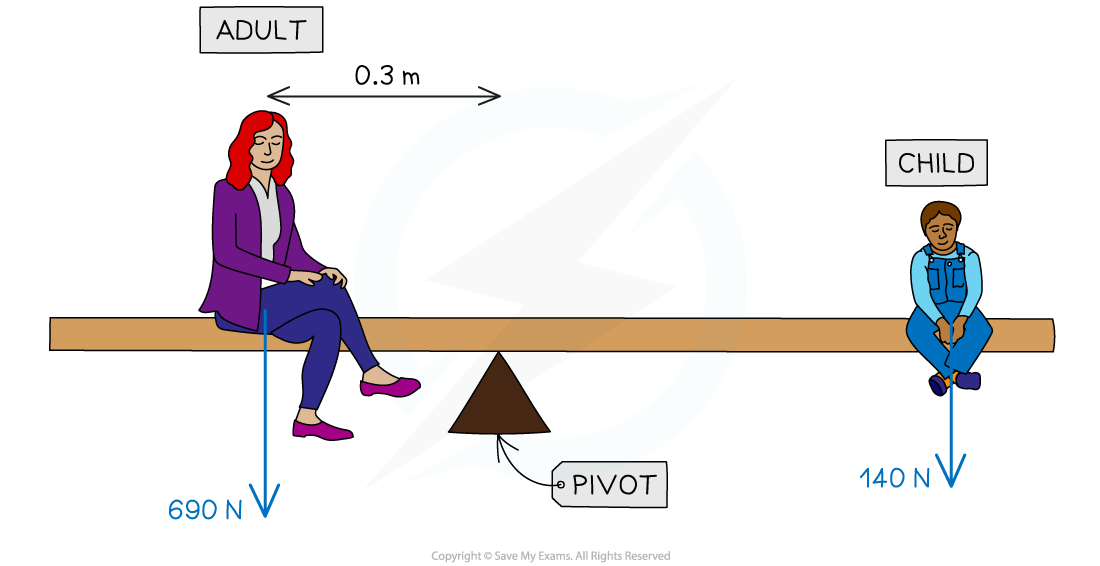
Calculate the distance the child must sit from the pivot for the see-saw to be balanced.
Answer:
Step 1: List the known quantities
Clockwise force (child), Fchild = 140 N
Anticlockwise force (adult), Fadult = 690 N
Distance of adult from the pivot, dadult = 0.3 m
Step 2: Write down the relevant equation
Moments are calculated using:
Moment = force × distance from pivot
For the see-saw to balance, the principle of moments states that
Total clockwise moments = Total anticlockwise moments
Step 3: Calculate the total clockwise moments
The clockwise moment is from the child
Moment of child (clockwise) = Fchild × dchild
Moment of child (clockwise) = 140 × dchild
Step 4: Calculate the total anticlockwise moments
The anticlockwise moment is from the adult
Moment of adult (anticlockwise) = Fadult × dadult
Moment of adult (anticlockwise) = 690 × 0.3 = 207 N m
Step 5: Substitute into the principle of moments equation
Moment of child (clockwise) = Moment of adult (anticlockwise)
140 × dchild = 207
Step 6: Rearrange for the distance of the child from the pivot
dchild = = 1.5 m
The child must sit 1.5 m from the pivot to balance the see-saw
Examiner Tips and Tricks
Make sure that all the distances are in the same units and that you’re considering the correct forces as clockwise or anticlockwise. In your WJEC GCSE you will not be expected to apply the principle of moments to a situation other than the balance beam on a pivot.

Unlock more, it's free!
Did this page help you?