Revision NotesPast Papers
GCSEPhysicsWJECRevision Notes2. Forces, Space & Radioactivity2.4 Further Motion ConceptsEquations of Motion

Equations of Motion (WJEC GCSE Physics): Revision Note

Ann Howell

Last updated

Equations of Motion

  • The equations of motion are used for objects in constant acceleration (or deceleration)

    • For example, an object falling under gravity without air resistance

  • Properties of this motion are calculated with the following variables:

    • u = initial velocity (m/s)

    • v = final velocity (m/s)

    • a = acceleration (m/s2)

    • x = distance travelled (m)

    • t = time (s)

An Example of the Use of Motion Variables

2-4-equations-of-motion-variables-example

A ball is dropped from rest, so the initial velocity is 0. The distance fallen is the distance travelled by the ball. The ball is falling and it is assumed there is no air resistance, so acceleration due to free fall is 10 m/s2.

How to use the equations of motion

  • Step 1: Write out the known and unknown variables given and use the context of the question to deduce any quantities that aren’t explicitly listed. For example:

    • In vertical motion a = g = ±10.0 m/s2 when an object is falling due to gravity

    • An object which starts at rest will have u = 0 when x = 0 and t = 0

    • An object that finishes at rest will have v = 0

  • Step 2: Choose one of the following equations which contain:

    • The one unknown quantity you need to find

    • The remaining variables are known quantities

  • Step 3: Convert any quantities into standard (SI) units, substitute into the equation and calculate the answer

    • For example, any distances in km must be converted into m or time in minutes converted into s

Equation 1:    v space equals space u space plus space a t

Equation 2:    x space equals space fraction numerator open parentheses u space plus space v close parentheses over denominator 2 end fraction t

Worked Example

The diagram below shows an arrangement to stop trains that are travelling too fast.

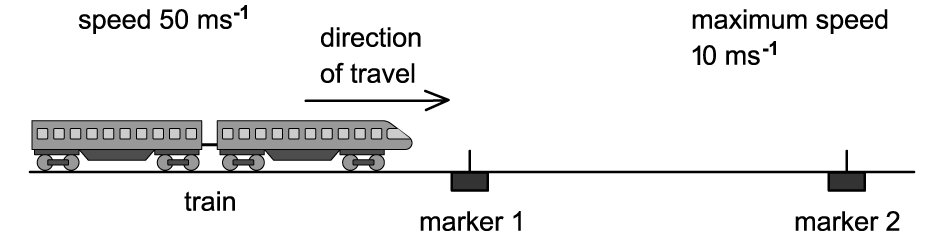
SUVAT Problems Worked Example

At marker 1, the driver must apply the brakes so that the train decelerates uniformly to pass marker 2 at no more than 10 m/s.

The train carries a detector that notes the times when the train passes each marker and will apply an emergency brake if the time between passing marker 1 and marker 2 is less than 20 s.

Trains coming from the left travel at a speed of 50 m/s.

Determine how far marker 1 should be placed from marker 2.

Answer:

Step 1: Write down the known and unknown variables

  • u = 50 m/s

  • v = 10 m/s

  • a =  unknown

  • x  = ? m

  • t = 20 s

Step 2: Choose the correct equation

  • u, v and t are known

  • We are asked to find x 

  • So the correct equation is:

x space equals space fraction numerator open parentheses u space plus space v close parentheses over denominator 2 end fraction t 

Step 3: Substitute the known quantities and solve to calculate the distance

x space equals space fraction numerator open parentheses 50 space plus space 10 close parentheses over denominator 2 end fraction space cross times space 20

x space equals space 30 space cross times space 20

x space equals space bold 600 bold space bold m

Worked Example

Higher Tier Only

Show that v = u + at is consistent with the definition of acceleration.

Answer:

Step 1: Define acceleration

  • Acceleration is defined as the rate of change of velocity

a space equals space fraction numerator open parentheses v space minus space u close parentheses over denominator t end fraction

Step 2: Rearrange to obtain the given equation

 at = (v − u)

 at + u = v

So, v = u + at

Examiner Tips and Tricks

This topic can seem a little daunting at first, but the best way to master this section is to practice as many questions as possible! You will normally be given the value of acceleration relevant to the question but you should be aware of the value of g = 10 m/s2. 

Remember only students studying the higher tier will be required to rearrange equations like in the second worked example.

More Equations of Motion

Higher Tier Only

  • The following two equations of motion are to be used by higher-tier students only

Equation 3:    x space equals space u t space plus space 1 half a t squared

Equation 4:    v squared space equals space u squared space plus space 2 a x

Worked Example

A cyclist is travelling directly east through a village, which is completely flat, at a velocity of 6 m/s. They then start to constantly accelerate at 2 m/s2 for 4 seconds.

(a) Calculate the distance that the cyclist covers in the 4 s acceleration period.

(b) Calculate the cyclist's final velocity after the 4 s interval of acceleration.  

Answer:

(a)

Step 1: List the known quantities

  • Initial velocity, u = 6 m/s

  • Acceleration, a = 2 m/s2 

  • Time, t = 4 s

  • Distance travelled = x (this needs to be calculated)

Step 2: Identify the best equation of motion to use

  • In this problem, the equation that links x, u, a, and t is

x space equals space u t space plus space 1 half a t squared 

Step 3: Substitute the known quantities into the equation

x = (6 × 4) + (0.5 × 2 × 42) = 24 + 16

Displacement:  x = 40 m 

(b)

Step 1: List the known quantities

  • Initial velocity, u = 6 m/s

  • Acceleration, a = 2 m/s2

  • Time, t = 4 s

  • Final velocity = v (this needs to be calculated)

Step 2: Identify and write down the equation to use

  • In this problem, the equation that links v, u, a, and t is:

v space equals space u space plus space a t 

Step 3: Substitute the known quantities into the equation

v = 6 + (2 × 4)

Final velocity:  v = 14 m/s

Worked Example

A science museum designed an experiment to show the fall of a feather in a vertical glass vacuum tube.

The time of fall from rest is 0.5 s.

WE - Projectile Motion Worked Example 1 question image, downloadable AS & A Level Physics revision notes

Use an appropriate equation of motion to calculate the length L of the tube.

Answer:

Step 1: List the known quantities

  • u = 0 m/s

  • v = unknown

  • a = 10 m/s2

  • x = L = ? m

  • t = 0.5 s

Step 2: Determine the equation that links these variables

x space equals space u t space plus space 1 half a t squared

L space equals space 1 half g t squared 

Step 3: Substitute the known quantities to calculate the length L

L space equals space 1 half space cross times space 10 space cross times space 0.5 squared

L space equals space bold 2 bold. bold 5 bold space bold m

Examiner Tips and Tricks

If you are not sure how to rearrange equations or substitute values into an equation then review this skill from your GCSE maths notes.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Safety Features of CarsNext:Momentum
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.