Revision NotesPast Papers
GCSEPhysicsWJECRevision Notes2. Forces, Space & Radioactivity2.4 Further Motion ConceptsConservation of Momentum

Conservation of Momentum (WJEC GCSE Physics): Revision Note

Ann Howell

Last updated

Conservation of Momentum

  • The principle of conservation of momentum states that:

    The total momentum before an interaction is equal to the total momentum after an interaction, if no external forces are acting on the objects

  • In this context, an interaction can be either:

    • A collision i.e. where two objects collide with each other

    • An explosion i.e. where a stationary object explodes into two (or more) parts

Collisions

  • For a collision between two objects:

    The total momentum before a collision = the total momentum after a collision

  • Before the collision:

    • The momentum is only generated by mass m  because it is the only moving object

    • If the right is taken as the positive direction, the total momentum of the system is m × u

  • After the collision:

    • Mass M also now has momentum

    • The velocity of m is now -v  (since it is now travelling to the left) and the velocity of M  is V

    • The total momentum is now the momentum of M + the momentum of m

    • This is (M  × V) + (m  × -v) or (M  × V) – (m × v) written more simply

Momentum Before and After a Collision

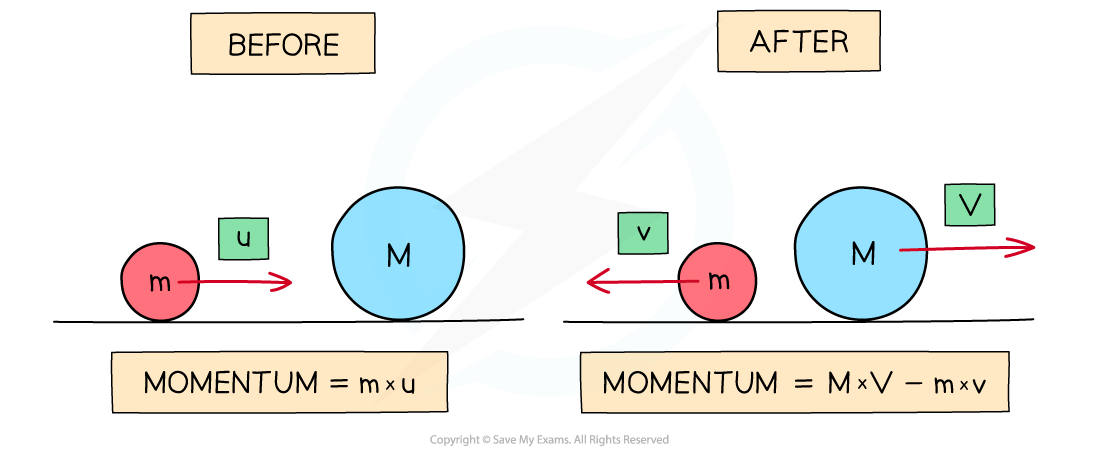
conservation-of-momentum-igcse-and-gcse-physics-revision-notes

The momentum of a system before and after a collision where the momentum before equals the momentum after

 Newton's Third Law in Collisions

  • According to Newton's Third Law:

    • When two objects collide, both objects will react, generally causing one object to speed up (gain momentum) and the other object to slow down (lose momentum)

Equal and Opposite Forces on Two Colliding Objects

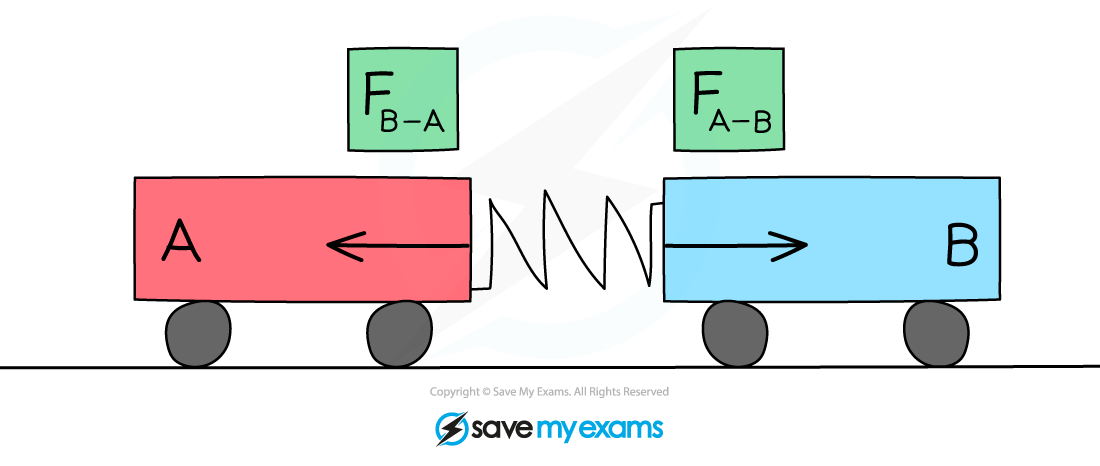
Newton’s-Third-Law-of-Motion, IGCSE & GCSE Physics revision notes

Newton's third law can be applied to collisions. Here the force of trolley A on B is equal and opposite to the force of trolley B on A.

  • Consider the collision between two trolleys, A and B:

    • Trolley A exerts a force on trolley B

    • Trolley B exert an equal force on trolley A in the opposite direction

  • This can be written as:

F subscript B minus A end subscript space equals space minus F subscript A minus B end subscript

Higher Tier Only

Explosions

  • Examples of explosions include:

    • A person jumping off a skateboard

    • A cannon or bullet being fired

    • A firework exploding

    • A person being thrown from a vehicle

    • The separation of space vehicles

  • As with collisions, the principle of conservation of momentum equations can be applied:

    • The mass of the separate objects = the mass of the original object

    • The initial velocity (and therefore, momentum) of the object is 0

  • Remember that velocity is a vector, so it considers the direction of the speed of each component

    • Some will travel in a positive direction and others in a negative direction

    • When they are all added together the resultant velocity = 0

Momentum of a Dynamite Explosion

2-4-momentum-in-an-explosion

The sum of the masses of the exploded pieces equals the mass of the original dynamite and the sum of the velocities of the separate pieces equals zero.

Worked Example

Higher Tier Only

The diagram shows a car and a van, just before and after the car collides with the van, which is initially at rest.

The car initially moves at a speed of 10 m/s, but this reduces to 2 m/s after the collision.

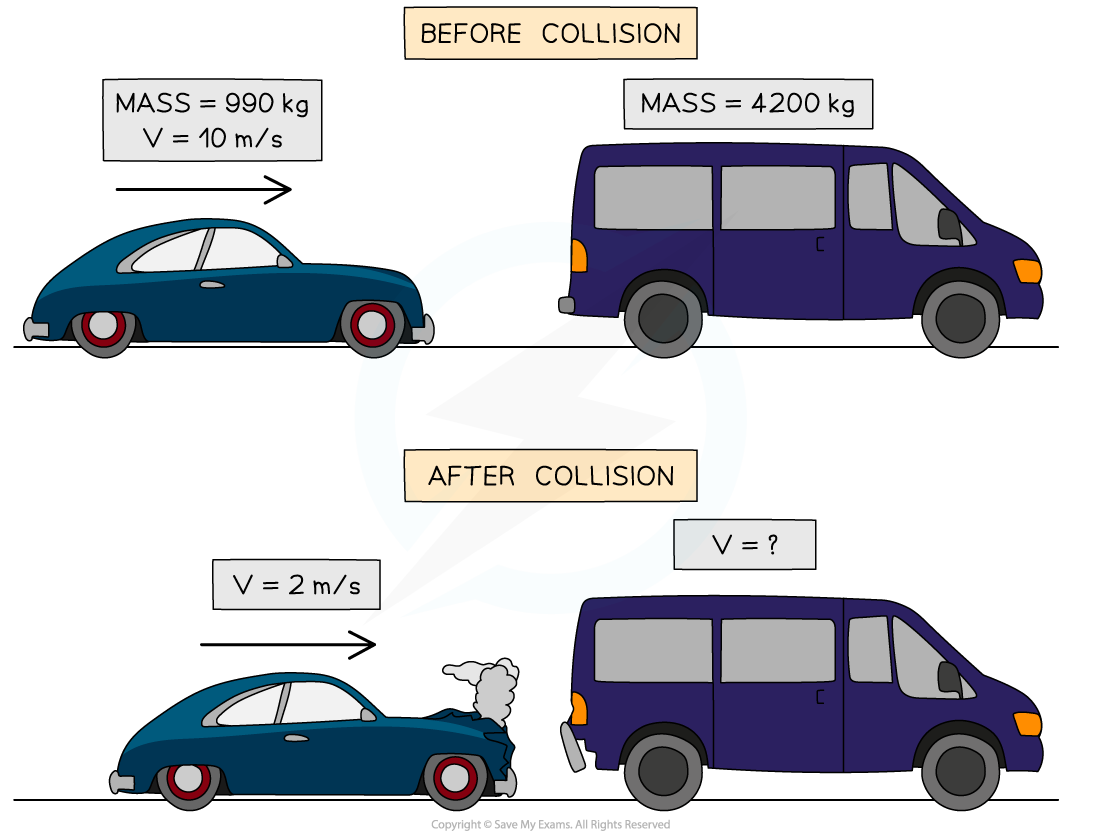
WE Conservation of Momentum Question image, downloadable IGCSE & GCSE Physics revision notes

The mass of the car is 990 kg and the mass of the van is 4200 kg.

Calculate the velocity of the van when it is pushed forward by the collision.

Answer:

Step 1: State the principle of the conservation of momentum

Total momentum before a collision = total momentum after a collision 

Step 2: Calculate the total momentum of the car and van before the collision

Momentum:  p = mv

  • Initial momentum of the car:

pcar = 990 × 10 = 9900 kgm/s

  • Initial momentum of the van:

pvan = 0 (the van is at rest, so p = v = 0)

  • Total momentum before collision:

pbefore =  pcar + pvan 

pbefore = 9900 + 0 = 9900 kg m/s

Step 3: Calculate the total momentum of the car and van after the collision

  • Final momentum of the car:

pcar = 990 × 2 = 1980 kg m/s

  • Final momentum of the van:

pvan = 4200 × v

  • Total momentum after collision:

pafter = 1980 + 4200v

Step 4: Rearrange the conservation of momentum equation for the velocity of the van

pbefore = pafter

9900 = 1980 + 4200v

9900 − 1980 = 4200v

v space equals space fraction numerator 9900 space minus space 1980 over denominator 4200 end fraction

v = 1.9 m/s

Worked Example

A gun of mass 3 kg fires a bullet of 30 g at a speed of 175 m/s. 

2-4-we-firing-a-gun

As the bullet is fired, the gun moves back with a recoil speed v.

Calculate the recoil speed of the gun v.

Answer:

Step 1: List the known quantities:

  • Velocity of gun/bullet before firing = 0 m/s

  • Mass of gun, mgun = 3 kg

  • Mass of bullet, mbullet = 30 g = 0.03 kg

  • Velocity of bullet after firing , vbullet = 175 m/s

  • Velocity of gun after firing = v

Step 2: State the conservation of momentum equation

momentum before firing = momentum after firing

momentum before firing = velocity of gun/bullet before firing = 0

0 = (mgun × v) + (mbullet × vbullet)

Step 3: Substitute the known quantities into the equation

0 = (3 × v) + (0.03 × 175)

Step 4: Rearrange the equation to find the recoil speed of the gun

−3v = 5.25

v space equals space fraction numerator 5.25 over denominator negative 3 end fraction

v = −1.75 m/s

  • Therefore, the recoil speed of the gun is 1.75 m/s

Examiner Tips and Tricks

Remember any question with rearranging to obtain velocity is a higher-tier one. 

If it is not given in the question already, drawing a diagram of before and after helps keep track of all the masses and velocities (and directions) in the conservation of momentum questions.

Remember that velocity is a speed with a direction. The question asks for the speed, so you do not need to include the final speed in your answer.

Momentum & Kinetic Energy

Higher Tier Only

  • In both collisions and explosions, momentum is always conserved

    • Energy is always conserved too, but kinetic energy might not always be conserved

  • A collision (or explosion) is either:

    • Elastic – if the kinetic energy is conserved

    • Inelastic – if the kinetic energy is not conserved

  • Collisions are instances when objects collide with each other:

    • Elastic collisions are usually when the colliding objects do not stick together and then they move in opposite directions

    • Inelastic collisions are usually when colliding objects stick together after the collision

Elastic and Inelastic Collisions

Elastic & Inelastic Collisions

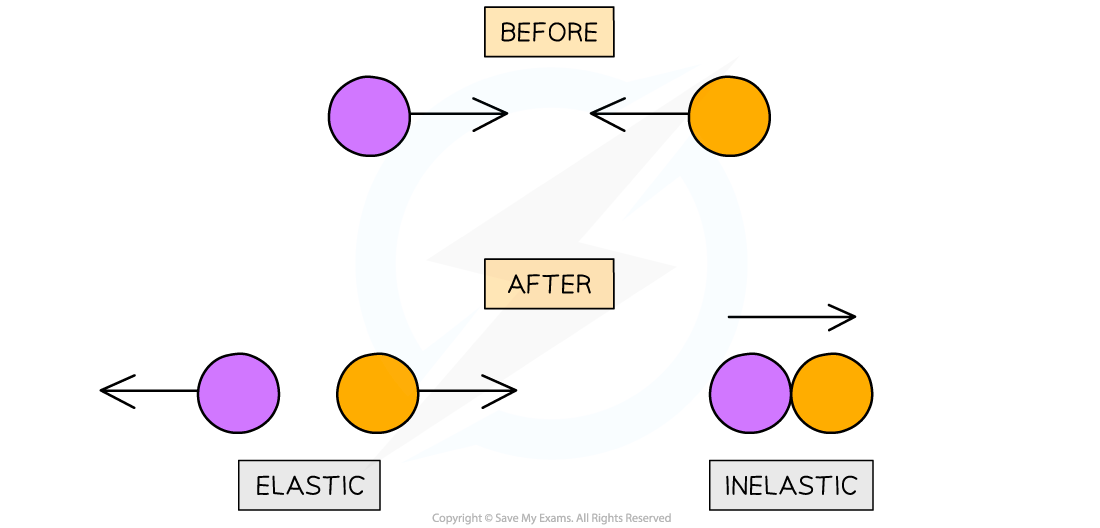
Elastic collisions are where two objects move in opposite directions. Inelastic collisions are where two objects stick together

  • To find out whether a collision is elastic or inelastic, compare the kinetic energy before and after the collision

  • The equation for kinetic energy is:

K E space equals space 1 half m v squared

  • Where:

    • KE = kinetic energy (J)

    • m = mass (kg)

    • v = velocity (m/s)

Worked Example

Two similar spheres, each of mass m and velocity v are travelling towards each other. The spheres have a head-on elastic collision.

we-elastic-collision

What is the total kinetic energy after the impact?

A. 1 half m v squared

B. 0

C. m v squared

D. 2 m v

Answer: C

Step 1: Consider the meaning of an elastic collision

  • In an elastic collision, kinetic energy is conserved, so:

kinetic energy before = kinetic energy after

Step 2: Obtain an equation in terms of kinetic energy before and kinetic energy after

kinetic energy before = 1 half m v squared space plus space 1 half m v squared space equals space m v squared

So, kinetic energy after = m v squared

Worked Example

Trolley A of mass 0.80 kg collides head-on with stationary trolley B at a speed 3.0 m/s. Trolley B has twice the mass of trolley A. The trolleys stick together and travel at a velocity of 1.0 m/s.

Show that this is an inelastic collision.

2-4-we-collision-type

Answer:

Step 1: State the known quantities

  • Mass of trolley A, MA = 0.80 kg

  • Mass of trolley B, MB = 2MA = 2 × 0.80 = 1.60 kg

  • Velocity of trolley A, VA = 3.0 m/s

  • Velocity of trolley B, VB = 1.0 m/s

Step 2: Recall the kinetic energy equation

K E thin space equals space 1 half m v squared 

Step 3: Calculate the kinetic energy before the collision

K E subscript b e f o r e end subscript space equals space 1 half M subscript A open parentheses V subscript A close parentheses squared space plus space 1 half M subscript B open parentheses V subscript B close parentheses squared

K E subscript b e f o r e end subscript space equals space 1 half cross times space 0.8 space cross times space 3.0 squared space plus space 1 half space cross times space 1.6 space cross times space 0 squared

K E subscript b e f o r e end subscript space equals space 1 half cross times space 0.8 space cross times space 3.0 squared space plus space 0

K E subscript b e f o r e end subscript space equals space 3.6 J 

Step 4: Calculate the kinetic energy after the collision

K E subscript a f t e r end subscript space equals space 1 half M subscript A plus B end subscript open parentheses V subscript A plus B end subscript close parentheses squared

K E subscript a f t e r end subscript space equals space 1 half space cross times space 2.4 space cross times space 1.0 squared

K E subscript a f t e r end subscript space equals space 1.2 J 

Step 5: Interpret the calculations

  • Before the collision the total KE is 3.6 J, and after the collision the total KE is 1.2 J, so K E subscript b e f o r e space end subscript not equal to space K E subscript a f t e r space end subscript

  • Therefore, the collision is inelastic

Examiner Tips and Tricks

If an object is stationary or at rest, its initial velocity is 0, therefore, the momentum and kinetic energy are also equal to 0.

When a collision occurs in which two objects are stuck together, treat the final object as a single object with a mass equal to the sum of the masses of the two individual objects.

Despite velocity being a vector, kinetic energy is a scalar quantity and therefore will never include a minus sign - this is because in the kinetic energy formula, mass is scalar and the v2 will always give a positive value whether it's a negative or positive velocity.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Force & MomentumNext:The Principle of Moments
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.