Calculating Work Done in Stretching

When a spring is stretched by a force work is done by the spring
The work done in stretching a spring is equal to the elastic energy stored in the spring

2-3-stretched-spring

Work is done on a spring when it is stretched

$W = \frac{1}{2} F x$

Where:
- W = work done by the spring or elastic potential energy (J)
- F = force applied to stretch the spring (N)
- x = extension of the spring (m)
This is only valid for springs not stretched beyond their limit of proportionality

Work done is calculated from the area under a force-extension graph
The area under the graph forms a triangle shape
- Where the area of a triangle is $\frac{1}{2} \times base \times height$
So, the work done = area = $\frac{1}{2} \times extension \times force$

2-3-area-under-force-extension-graph

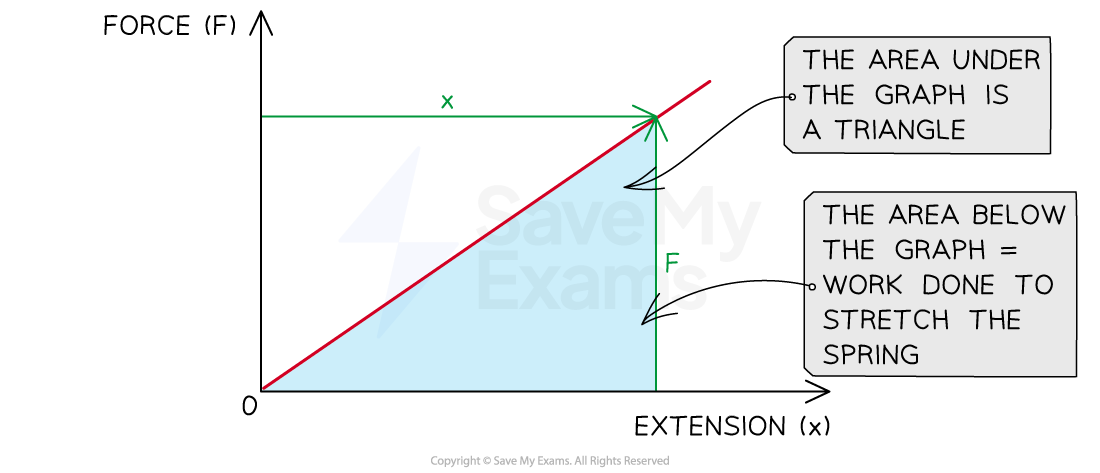
The area under the force-extension graph is a triangle. Calculating the area of the triangle gives the work done by the spring when stretched

A 250 g mass is attached to the bottom of a hanging spring. It stretches from 10.0 cm to 11.4 cm.

Gravitational field strength = 10 N/kg

Calculate the elastic potential energy stored by the stretched spring.

Answer

Step 1: Draw a diagram of the situation

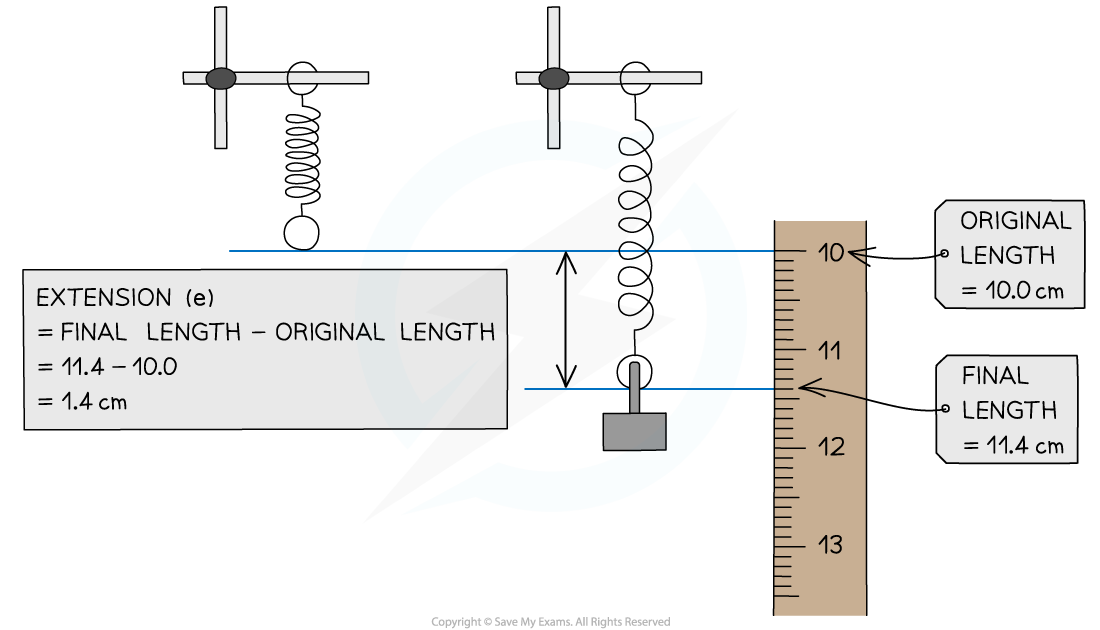
Step 2: List the known quantities

Step 3: Determine the extension of the spring in m

extension, x = final length − original length

x = 11.4 − 10.0 cm

x = 1.4 cm

x = 1.4 ÷ 100 = 0.014 m

Step 4: Determine the force on the spring

Weight = F = mg

F = 250 × 10

F = 2500 N

Step 5: Recall the equation for work done

$W = \frac{1}{2} F x$

Step 6: Calculate the work done

$W = \frac{1}{2} \times 2500 \times 0.014$

$W = 17.5$ J

Calculating Work Done in Stretching (WJEC GCSE Physics)