Gas Laws (WJEC GCSE Physics): Revision Note

Behaviour of Gases with Changing Conditions

Pressure & Volume

• For a gas at constant temperature:

  • Pressure increases if the volume decreases

  • Pressure decreases if the volume increases

  • Pressure and volume are inversely proportional

Graph of Relationship Between Volume and Pressure

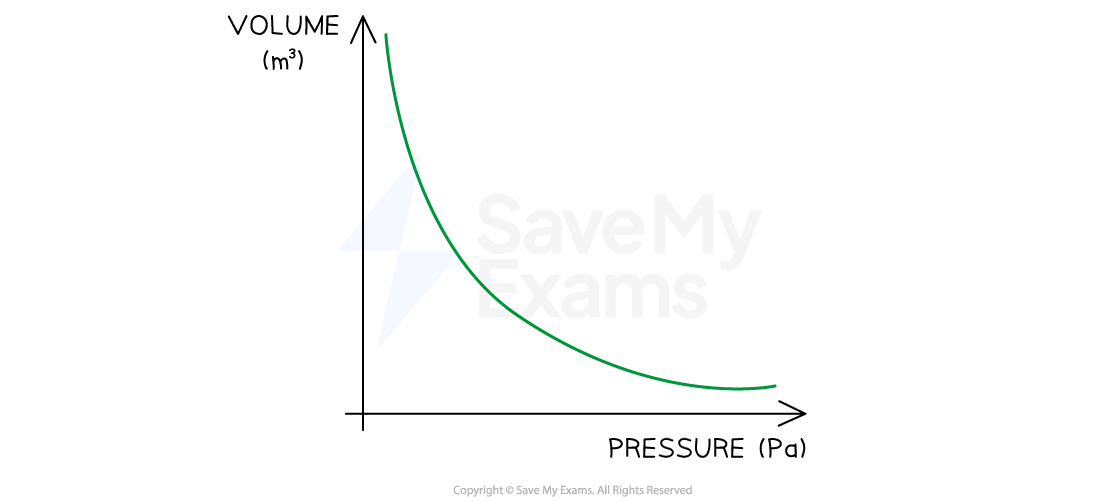
As pressure increases, volume decreases and vice versa. The curved shape of the graph shows an inversely proportional relationship

Pressure & Temperature

• For a gas at constant volume:

  • The pressure increases if the temperature increases

  • The pressure decreases if the temperature decreases

  • Pressure and temperature are directly proportional

Graph of Relationship Between Pressure and Temperature on the Kelvin Scale

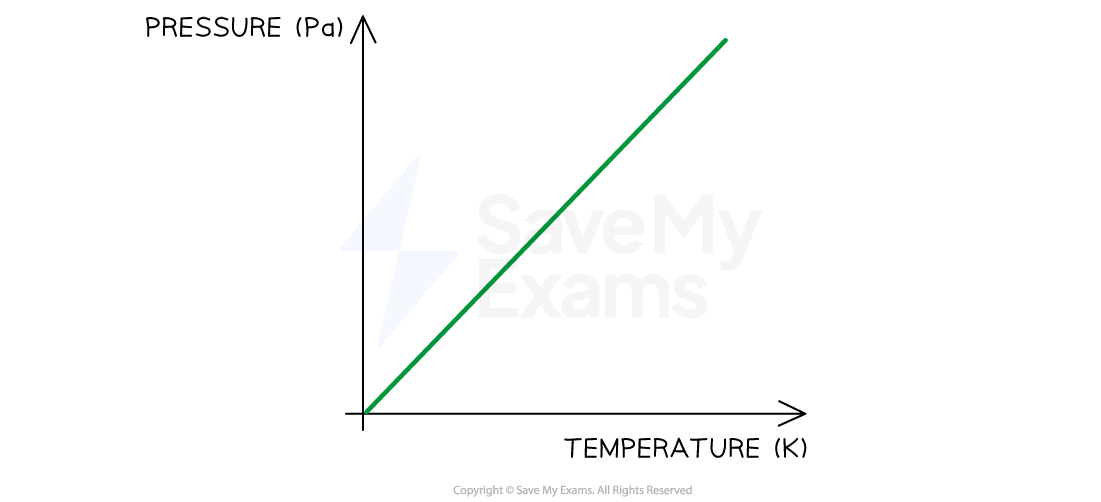
As temperature increases, pressure increases. The shape of the graph shows a directly proportional relationship

Volume and Temperature

• For a gas at constant pressure:

  • The volume will increase if the temperature is increased

  • The volume will decrease if the temperature is decreased

  • Volume and temperature are directly proportional

Graph of Relationship Between Volume and Temperature on the Kelvin Scale

As temperature increases, volume increases. The shape of the graph shows a directly proportional relationship

Explaining Changes in Pressure

Changes in Pressure With Changing Volume

• In a gas, the particles are spread out with spaces between them

• This makes a gas easy to expand and compress

• When a gas is compressed, the volume is decreased

  • The density of the gas increases

  • The volume of the container has decreased but the number of particles has remained the same

  • This results in more frequent collisions with the container walls

  • So there is an increase in pressure

• When a gas is expanded, the volume is increased

  • The density of the gas decreases

  • The volume of the container has increased but the number of particles has remained the same

  • This results in less frequent collisions with the container walls

  • So there is a decrease in pressure

Compression of a Gas at Constant Volume

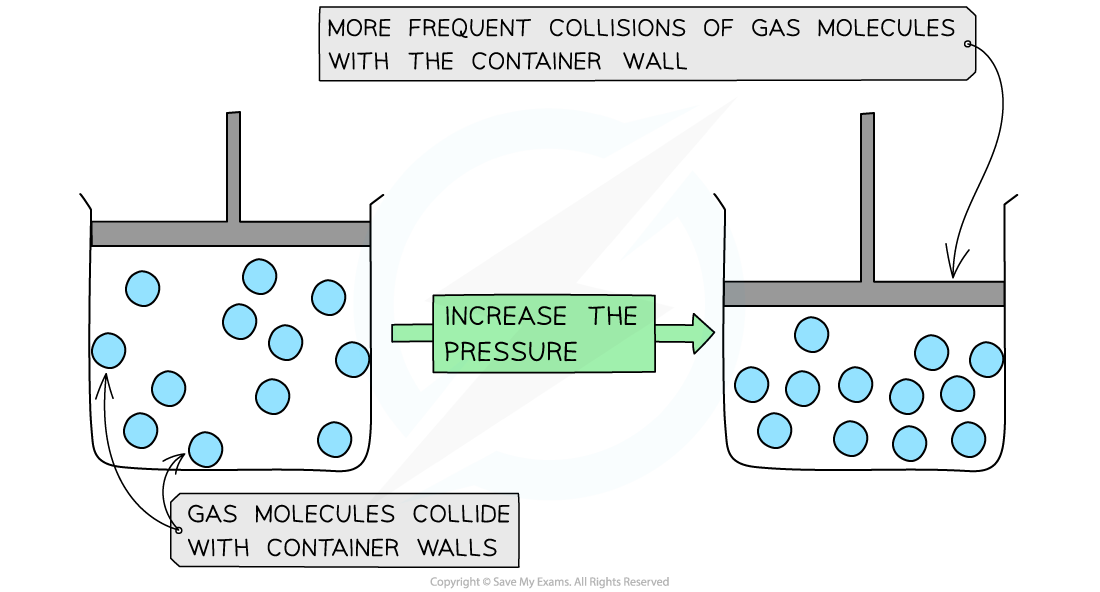
As the volume of the container is decreased, the gas particles collide more frequently with the walls of the container causing an increase in pressure 

• The key assumption is that the temperature and the mass (and number) of the particles remain the same

Pressure Changes with Changing Temperature

• The temperature of a substance is related to the average kinetic energy of its particles

• As a substance is heated, the particles gain more kinetic energy and move around faster

• When the temperature of a gas is increased, the pressure is increased

  • The particles of the gas gain more kinetic energy and move around faster

  • This results in more frequent collisions with the container walls

  • And the collisions have a greater force

  • This results in an increase in pressure

• When the temperature a gas is decreased, the pressure is decreased

  • The particles of the gas have less kinetic energy and move around slower

  • This results in less frequent collisions with the container walls

  • And the collisions have a lesser force

  • This results in a decrease in pressure

Heating a Gas at Constant Volume

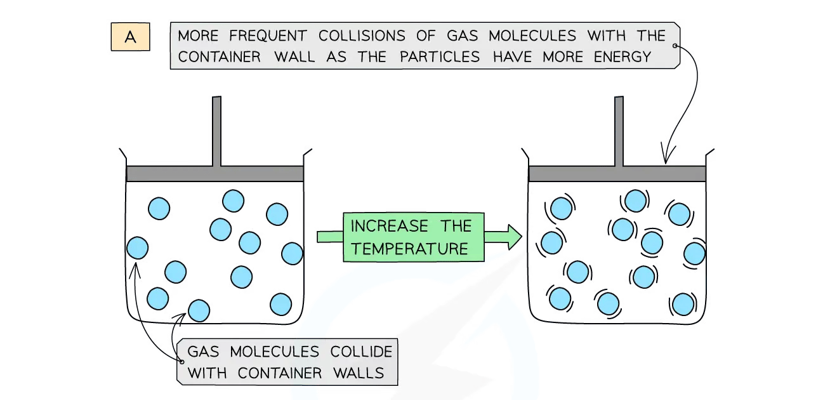
As the temperature of the gas is increased, the gas particles collide more frequently and more forcefully with the walls of the container, causing an increase in pressure 

• The pressure−temperature graph (and the volume−temperature graph) look a little different on the Celsius scale

  • The line only goes through the origin if the temperature is in K

  • On the Celsius scale, zero pressure is reached at absolute zero, −273 °C

Pressure-Temperature Graph on the Celsius Scale

The line does not go through the origin when the temperature is given in °C, zero pressure is reached at −273 °C

Gas Laws

Higher Tier Only

• For a fixed mass of a gas held at a constant temperature:

  • Pressure is inversely proportional to volume

• Therefore:

• Where:

  • p = pressure in pascals (Pa)

  • V = volume in metres cubed (m³)

Diagram Showing a Decrease in Pressure When Volume is Increased

Increasing the volume of a gas decreases its pressure

• The  equation can also be written as:

• Where:

  • p₁  = initial pressure in pascals (Pa)

  • V₁  = initial volume in metres cubed (m³)

  • p₂  = final pressure in pascals (Pa)

  • V₂  = final volume in metres cubed (m³)

• This equation is sometimes referred to as Boyle's Law

• It is used to compare the pressure and volume before and after a change in a gas

Diagram Illustrating Boyle's Law

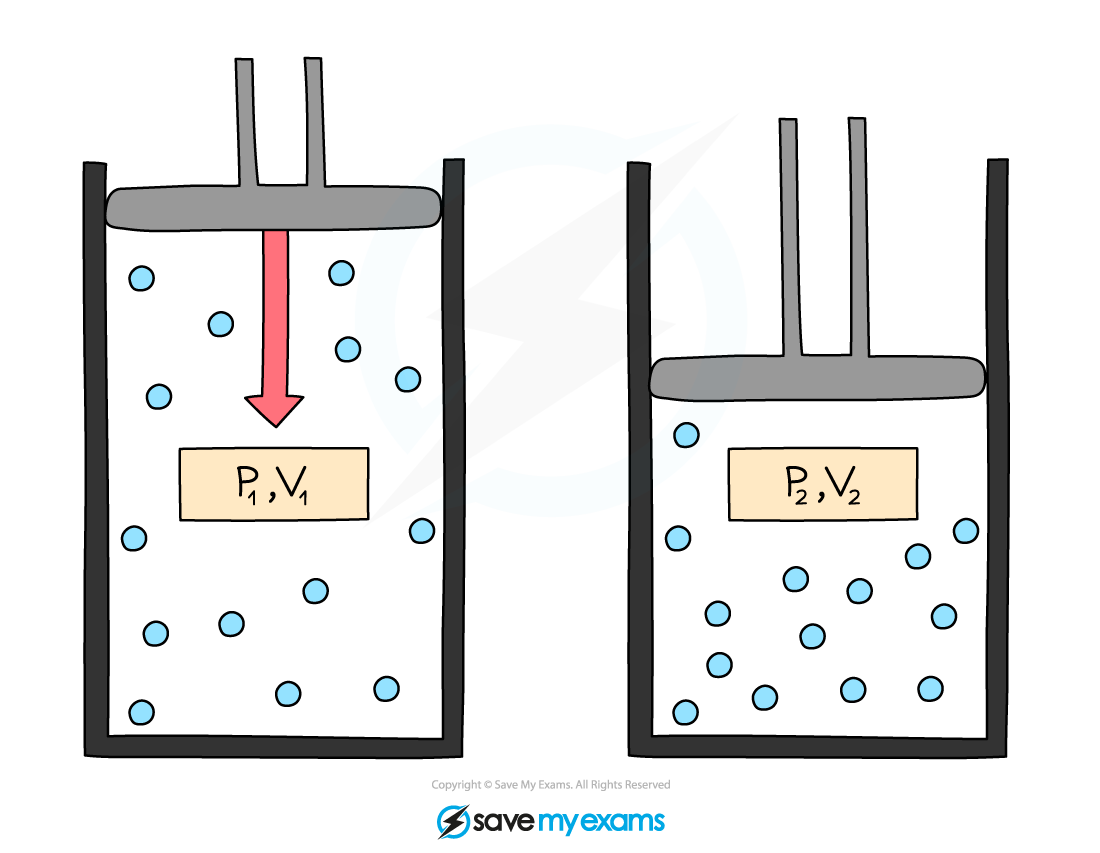
The initial pressure and volume are the values before the change, and the final pressure and volume are the values after the change