Sankey Diagrams & Efficiency (WJEC GCSE Physics)

 

• The efficiency of a system is a measure of the amount of wasted energy in an energy transfer

• Efficiency is defined as:

The ratio of the useful power or energy output from a system to its total power or energy input

• If a system has high efficiency, this means most of the energy transferred is useful
• If a system has low efficiency, this means most of the energy transferred is wasted

 

• The overall efficiency of a typical thermal power station is approximately 30%
  • This means that 70% is wasted energy
  • At each stage of the electricity production process, energy is dissipated to the surroundings

 

• Sankey diagrams are often used to show the efficiency of energy transfers

Sankey Diagram for a Gas-fired Power Station

Sankey diagrams show the efficiency of a system

 

• Key features of Sankey diagrams:
  • The width of the arrows represents the amount of energy 
  • The flat end of the arrow represents the total energy input
  • The downward arrows represent wasted energy output
  • The horizontal arrows represent the useful energy output

Energy Distribution in a Sankey Diagram

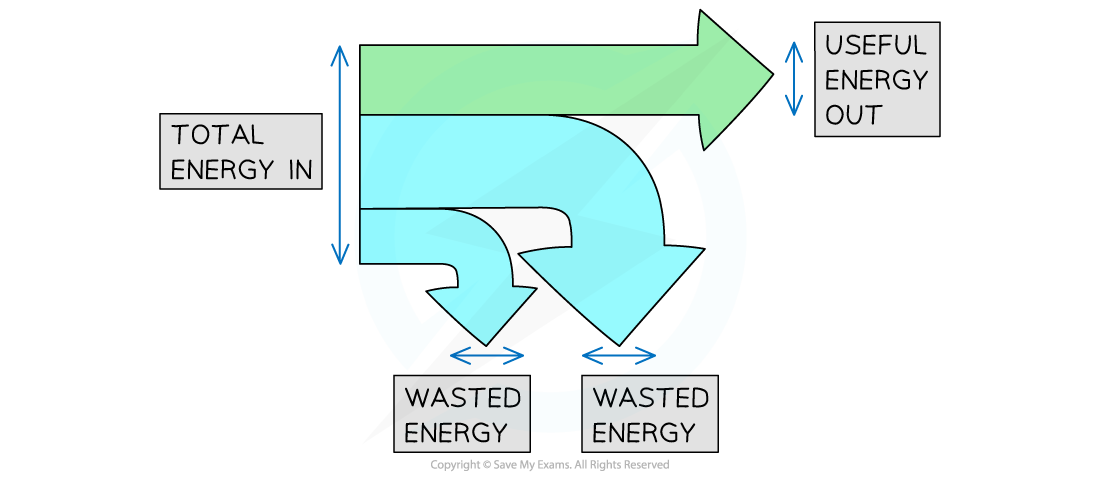
Total energy input, useful and wasted energy outputs on a Sankey diagram

• Efficiency is represented as a percentage, and can be calculated using the equation:

• The efficiency equation can also be written in terms of power:

• Where power is defined as the energy transferred per unit of time