Current & Voltage Relationships (WJEC GCSE Physics): Revision Note

Current & Voltage Relationships

• Resistance is defined as the opposition to current:

• Resistance occurs because the free electrons flowing in the circuit (current) collide with the metal ions in the wire which slows them down or resists their flow

  • The higher the resistance of a circuit, the lower the current

  • This means that good conductors have a low resistance and insulators have a high resistance

• The symbol for resistance is R

• It is measured in ohms (Ω)

  • Ω is the Greek capital letter ‘Omega’

• The resistance of a circuit can be increased by adding resistors (or variable resistors) to it

• Every electrical component has a resistance, even wires

  • In exam questions, the resistance of the wires and batteries are assumed to be negligible

Diagram Showing How Resistance Affects Current

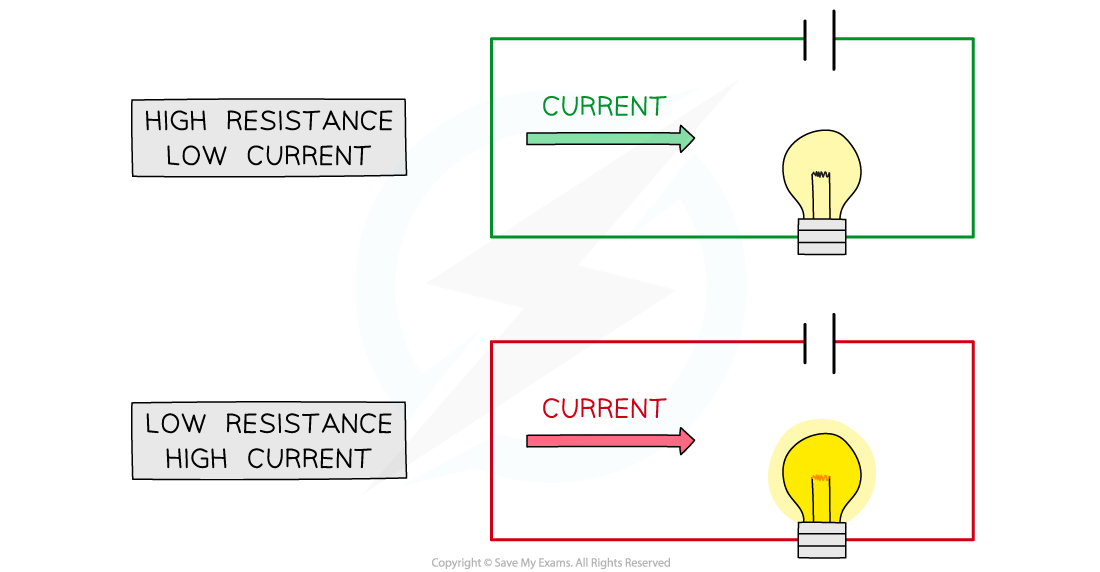
When a circuit has a high resistance, a lower current will flow, and vice versa

• Current, , voltage,V, and resistance, R, all affect one another

• For a fixed resistance, current is directly proportional to voltage

  • If voltage doubles, current doubles

• For a fixed voltage, current is inversely proportional to resistance

  • If resistance doubles, current halves

• These relationships are described using the following equation

• Where:

  • = current measured in amps (A)

  • V = voltage measured in volts (V)

  • R = resistance measured in ohms (Ω)

•  This equation is sometimes called the resistance equation or Ohm's law

Equation Triangle for Current, Voltage and Resistance

• Students taking the Higher Tier exam paper will need to be able to rearrange this equation

• The equation triangle can help with rearranging the equation if you need support

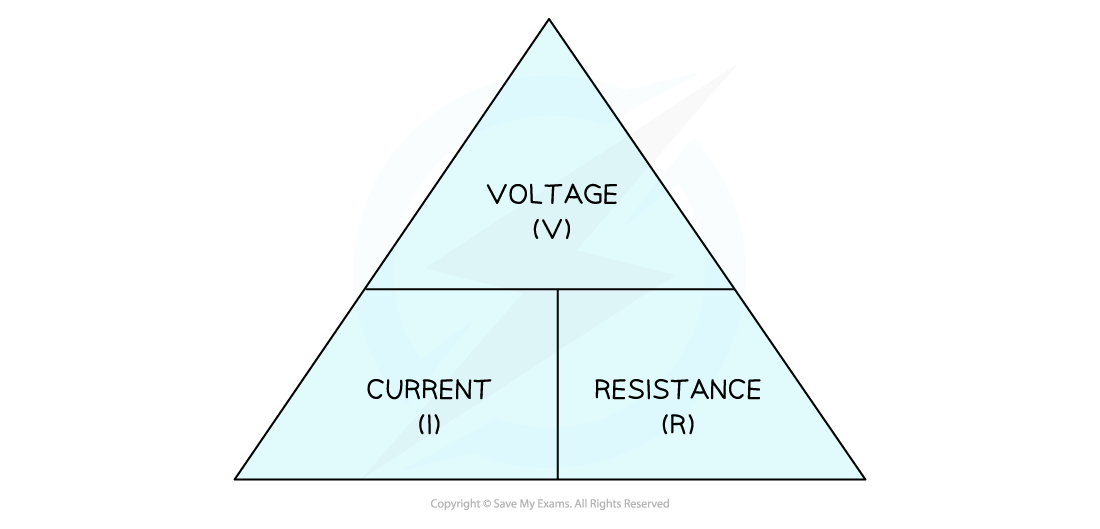
Cover up the variable you need to calculate, and the triangle shows you how the equation is arranged

• To use an equation triangle:

  • Cover the variable to need to calculate

  • The remaining variables are positioned correctly for that equation

  • Multiplication across the base of the triangle

  • Division of the top of the triangle by the bottom

• For example:

  • To calculate voltage, 

  • To calculate resistance,