Estimating Braking Distances, Speeds & Accelerations (OCR GCSE Physics A (Gateway)) : Revision Note
Estimating Stopping Distances
For a given braking force, the speed of a vehicle determines the size of the stopping distance
The greater the speed of the vehicle, the larger the stopping distance
The image below shows how the stopping distance of a typical family car increases with increasing speed:
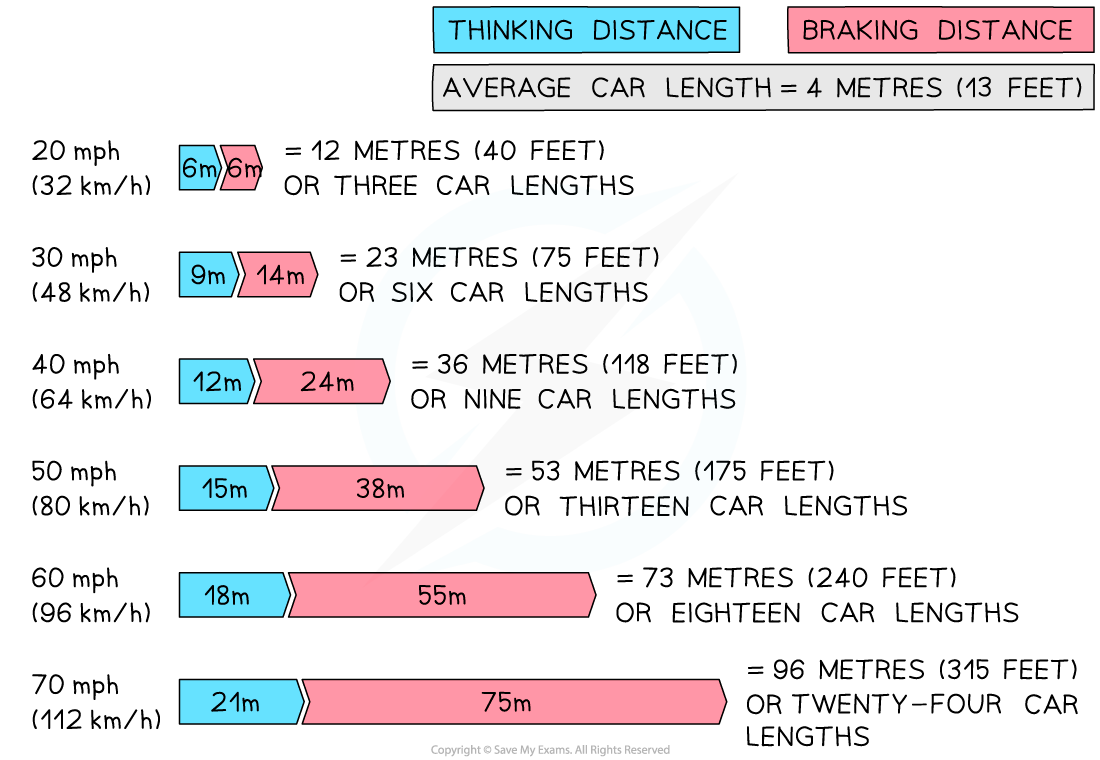
A vehicle's stopping distance increases with speed. At a speed of 20 mph the stopping distance is 12 m, whereas at 60 mph the stopping distance is 73 m (reproduced from the UK Highway Code)
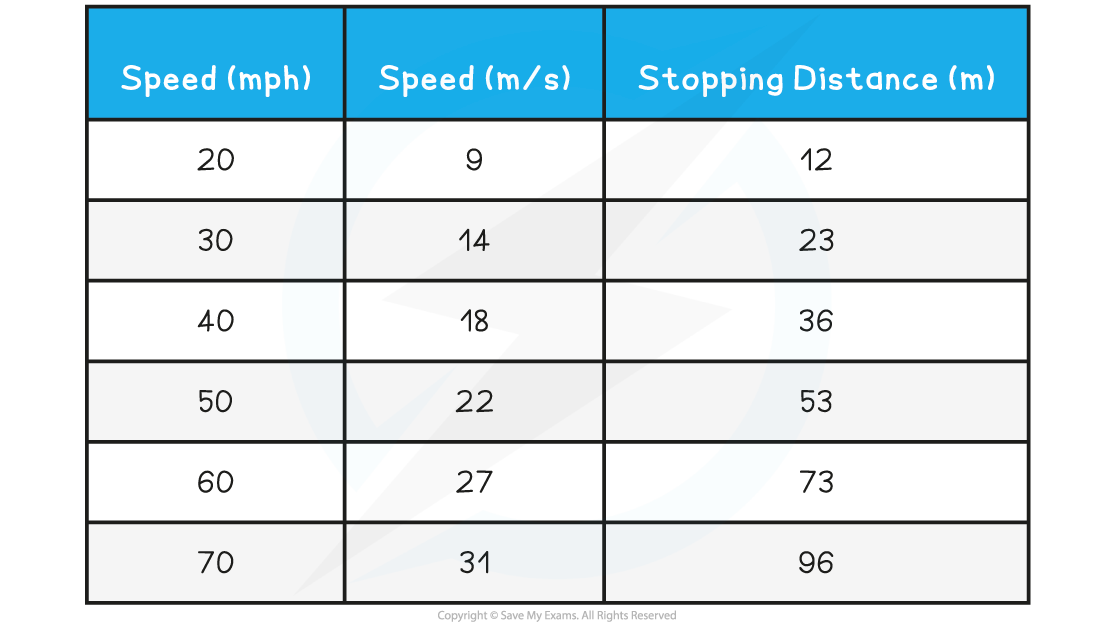
Velocity-Time Graphs for Stopping Distance
The velocity-time graph below shows how the velocity of a car will typically change during an emergency stop
Graph showing how the velocity typically changes as a vehicle comes to an emergency stop
While the driver reacts (the time taken to press the brakes is called the reaction time), the vehicle continues moving at a constant velocity
The area underneath the graph during this time represents the thinking distance
As soon as the brakes are applied, the vehicle decelerates to a halt
The area underneath the graph during this time represents the braking distance
Worked Example
While driving at a speed of 35 m/s, a driver sees an obstacle in the road at time t = 0. The velocity−time graph below shows how the speed of the car changes as the driver reacts and slams on the brakes, bringing the car to a halt.

Determine:
(a) The braking distance of the car
(b) The driver's reaction time
Answer:
Part (a)
Step 1: Identify the section of the graph which represents the braking distance
The area under a velocity-time graph represents distance travelled
The braking distance of the car is the distance travelled under the braking force
This area of the graph is shaded below:
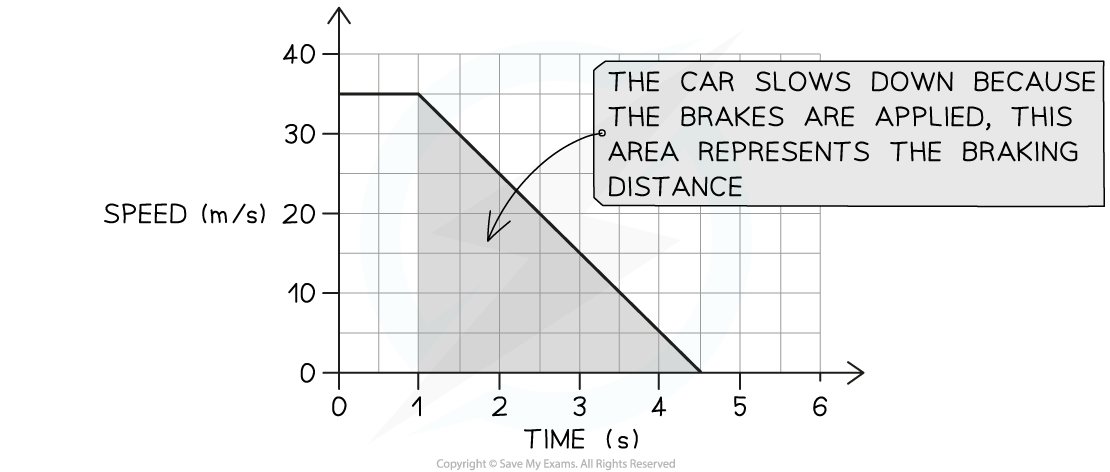
The braking distance of the car is the area shaded because the car decelerates once the brakes are applied
Step 2: Calculate the area under the graph during the car's deceleration
The area is a triangle, so the braking distance is given by:
Braking distance = Area = ½ × base × height
Braking distance = ½ × (4.5 – 1) × 35 = 61.3 m
Part (b)
Step 1: Determine how long the driver takes before the brakes are applied
Between seeing the obstacle and applying the brakes, 1 second passes
This sequence of events is labelled on the graph below:
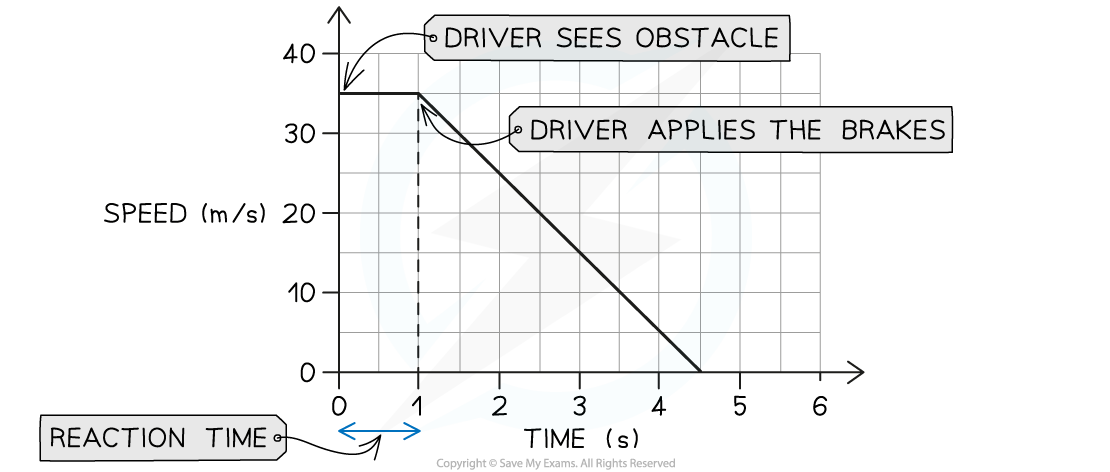
The driver's reaction time is the time between the moment they see the obstacle to the moment the brakes are applied
Therefore, the driver's reaction time is 1 s
Examiner Tips and Tricks
The thinking and stopping distance definitions are often confused with each other. Remember that the thinking distance is to do with the driver whilst the stopping distance is to do with the vehicle and road conditions
Estimating Braking Speeds & Accelerations
Worked Example
The graph below shows how the thinking distance of a driver depends on the speed of the car.
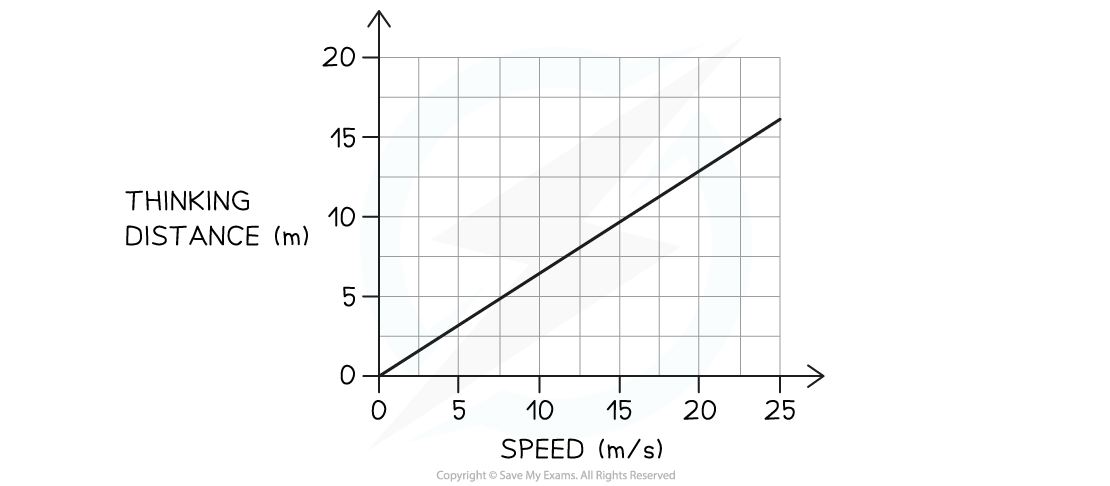
(a) Describe the connection between thinking distance and speed.
(b) Some people drive when they are tired, despite warnings against doing so. Draw a new line on the graph to show how thinking distance varies with speed for a tired driver.
Answer:
Part (a)
Step 1: Check if the line is straight and if it goes through the origin
The graph shows a straight line through the origin
Therefore, the thinking distance is directly proportional to the speed of the car
Part (b)
Step 1: Recall the factors which affect the thinking distance
Three additional factors affect the thinking distance, because they affect human reaction time:
Tiredness
Distractions
Intoxication
Hence, a tired driver's reaction time is greater (i.e. it takes longer for them to react)
Step 2: Draw a line that shows greater thinking distance for the same speed
At the same speed, a tired driver's thinking distance will be greater than a driver who is alert
This means a line should be drawn with a steeper gradient, as shown below:
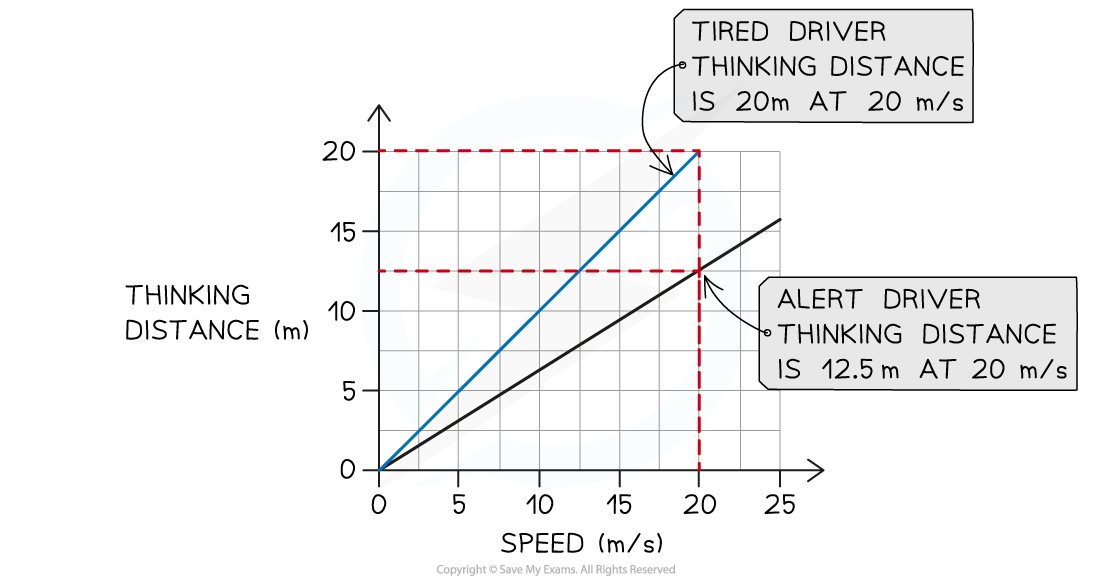
Worked Example
A passenger travels in a car at a moderate speed. The vehicle is involved in a collision, which brings the car (and the passenger) to a halt in 0.1 seconds. Estimate:
a) The acceleration of the car (and the passenger)
b) The force on the passenger
Answer:
Part (a)
Step 1: Estimate the required quantities and list the known quantities
A moderate speed for a car is about 50 mph or 20 m/s
Initial velocity ~ 20 m/s
Final velocity = 0 m/s
Time, t = 0.1 s
Step 2: Calculate the change in velocity of the car (and the passenger)
change in velocity = Δv = final velocity − initial velocity
Δv = 0 − 20
Δv = −20 m/s
Step 3: Calculate the acceleration of the car (and the passenger) using the equation:
Step 4: Calculate the deceleration
a = −20 ÷ 0.1
a ~ −200 m/s2
Part (b)
Step 1: Estimate the required quantities and list the known quantities
An adult person has a mass of about 70 kg
Mass of the passenger, m ~ 70 kg
Acceleration, a = −200 m/s2
Step 2: State Newton's second law
This question involves quantities of force, mass and acceleration, so the equation for Newton's second law is:
F = ma
Step 3: Calculate an estimate for the decelerating force
F = 70 × −200
F ~ −14 000 N
Examiner Tips and Tricks
Remember that resultant force is a vector quantity. Examiners may ask you to comment on why its value is negative - this happens when the resultant force acts in the opposite direction to the object's motion.
In the worked example above, the resultant force opposes the passenger's motion, slowing them down (decelerating them) to a halt, this is why it has a minus symbol.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?