Revision NotesExam QuestionsPast Papers
GCSEPhysicsOCRPhysics A (Gateway)Revision Notes2. ForcesMotionCalculating Uniform Acceleration

Calculating Uniform Acceleration (OCR GCSE Physics A (Gateway))

Revision Note

Ashika

Written by: Ashika

Reviewed by: Caroline Carroll

Calculating Uniform Acceleration

  • Acceleration is defined as the rate of change of velocity

  • In other words, it describes how much an object's velocity changes every second

  • The equation below is used to calculate the average acceleration of an object:

  • Where:

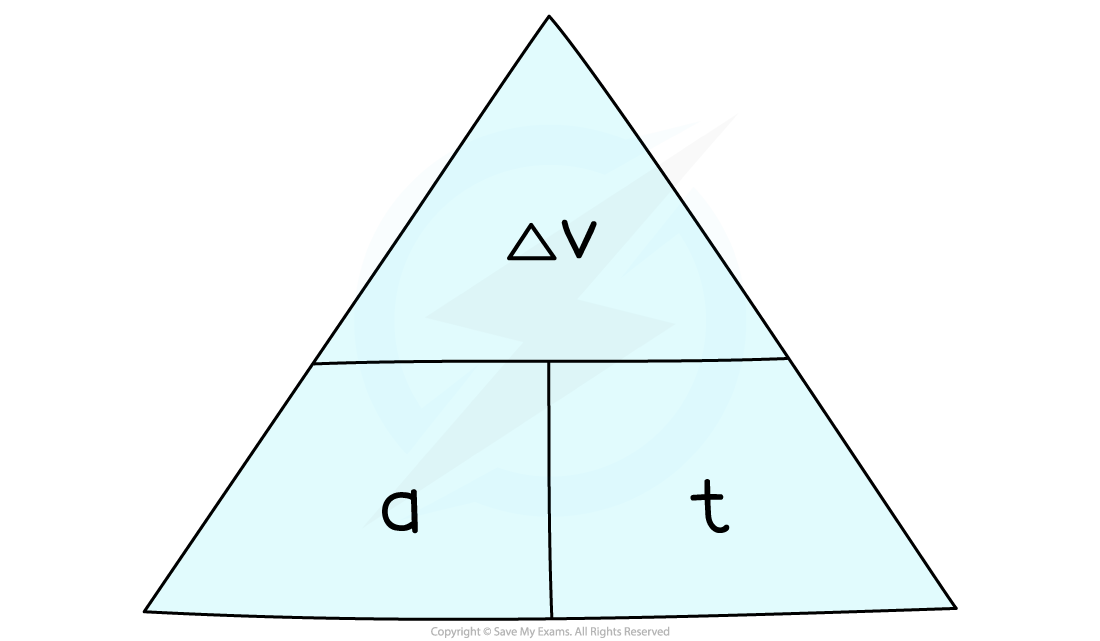
    • a = acceleration in metres per second squared (m/s2)

    • Δv = change in velocity in metres per second (m/s)

    • t = time taken in seconds (s)

  • The change in velocity is found by the difference between the initial and final velocity, as written below:

change in velocity = final velocity − initial velocity

Δv = v − u

  • Where:

    • v = final velocity in metres per second (m/s)

    • u = initial velocity in metres per second (m/s)

  • The equation for acceleration can be rearranged with the help of a formula triangle as shown:

Acceleration Formula Triangle, downloadable IGCSE & GCSE Physics revision notes

Speeding Up & Slowing Down

  • An object that speeds up is accelerating

  • An object that slows down is decelerating

  • The acceleration of an object can be positive or negative, depending on whether the object is speeding up or slowing down

    • If an object is speeding up, its acceleration is positive

    • If an object is slowing down, its acceleration is negative (sometimes called deceleration)

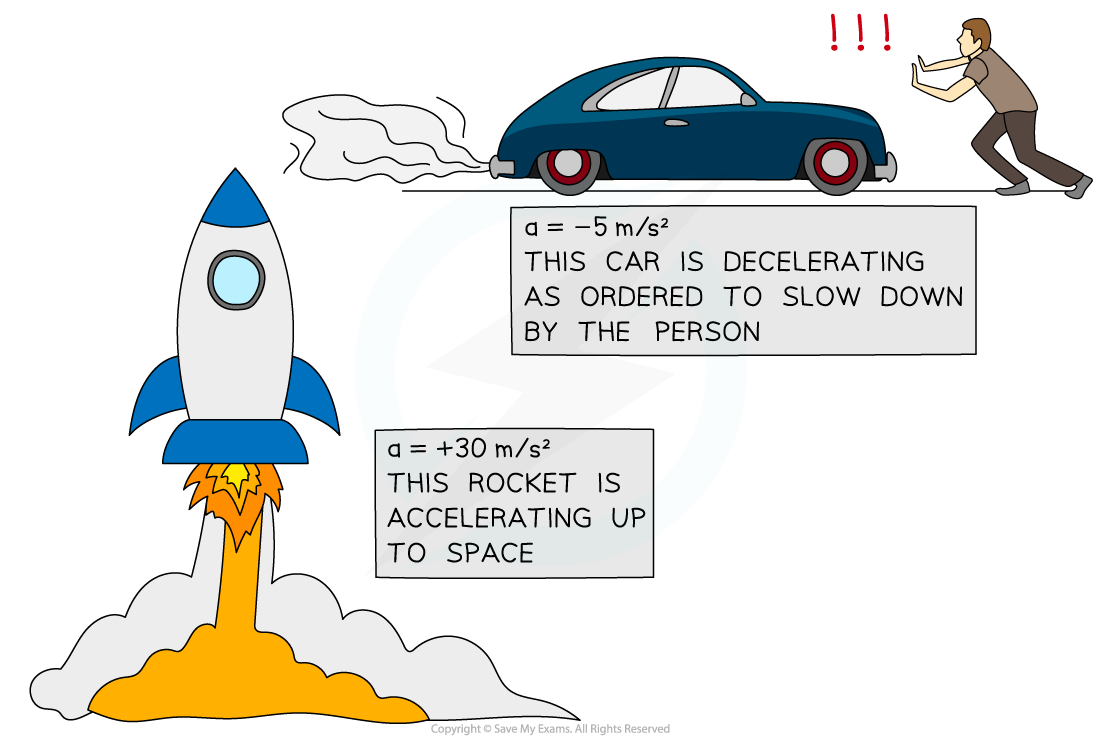
Acceleration Examples, downloadable IGCSE & GCSE Physics revision notes

A rocket speeding up (accelerating) and a car slowing down (decelerating)

Uniform Acceleration

  • The following equation of motion applies to objects moving with uniform (constant) acceleration:

(final speed)2 − (initial speed)2 = 2 × acceleration × distance travelled

v squared minus u squared equals space 2 cross times a cross times x

  • Where:

    • x = distance travelled in metres (m)

    • u = initial speed in metres per second (m/s)

    • v = final speed in metres per second (m/s)

    • a = acceleration in metres per second squared (m/s2)

  • This equation is used to calculate quantities such as initial or final speed, acceleration, or distance travelled in cases where the time taken is not known

Worked Example

A Japanese bullet train decelerates at a constant rate in a straight line. The velocity of the train decreases from 50 m/s to 42 m/s in 30 seconds.

(a) Calculate the change in velocity of the train.

(b) Calculate the deceleration of the train, and explain how your answer shows the train is slowing down.

Answer:

Part (a)

Step 1: List the known quantities

  • Initial velocity = 50 m/s

  • Final velocity = 42 m/s

Step 2: Write the relevant equation

change in velocity = final velocity − initial velocity

Step 3: Substitute values for final and initial velocity

change in velocity = 42 − 50 = −8 m/s

Part (b)

Step 1: List the known quantities

  • Change in velocity, Δv = − 8 m/s

  • Time taken, t = 30 s

Step 2: Write the relevant equation

straight a equals fraction numerator straight capital delta straight v space over denominator straight t end fraction

Step 3: Substitute the values for change in velocity and time

a = −8 ÷ 30 = −0.27 m/s

Step 4: Interpret the value for deceleration

  • The answer is negative, which indicates the train is slowing down

Worked Example

A car accelerates steadily from rest at a rate of 2.5 m/s2 up to a speed of 16 m/s. Calculate how far the car moves during this period of acceleration.

Answer:

Step 1: Identify and write down the equation to use

  • The question says that the car 'accelerates steadily' - so the equation for uniform acceleration can be used:

v2 − u2 = 2 × a × x

Step 2: List the known quantities

  • Initial speed, u = 0 m/s (the car starts from rest)

  • Final speed, v = 16 m/s

  • Acceleration, a = 2.5 m/s2

  • Distance, x = ? (this needs to be calculated)

Step 3: Substitute known quantities into the equation and simplify where possible

162 − 02 = (2 × 2.5 × x)

  • This can be simplified to:

256 = 5 × x

Step 4: Rearrange the equation to work out the distance travelled

x = 256 ÷ 5

x = 51.2 m

Kinetic Energy

  • The kinetic energy (Ek or KE) of an object (also known as its kinetic store) is defined as:

The energy an object has as a result of its mass and speed

  • This means that any object in motion has kinetic energy

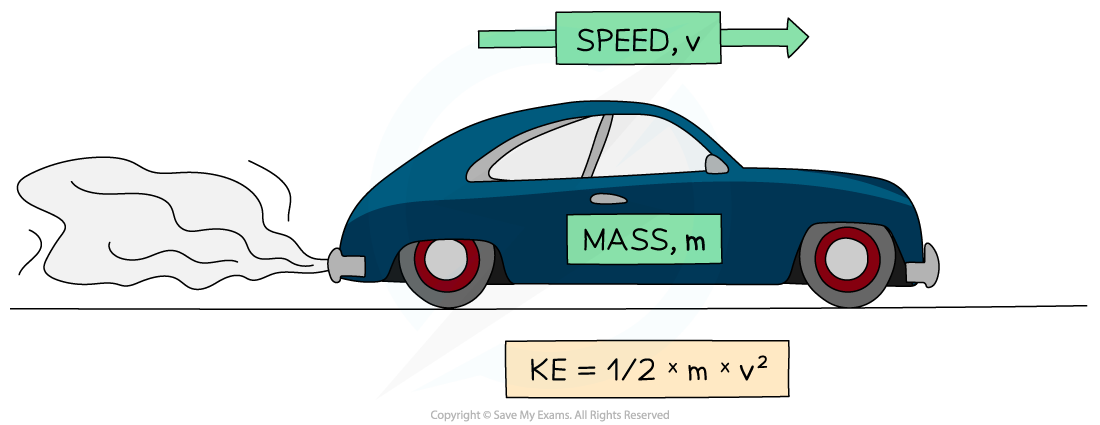
Kinetic Energy Car, downloadable AS & A Level Physics revision notes

  • Kinetic energy can be calculated using the equation:

Ek = ½ × m × v2

  • Where:

    • Ek = kinetic energy in Joules (J)

    • m = mass of the object in kilograms (kg)

    • v = speed of the object in metres per second (m/s)

  • Therefore, an acceleration will result in a change of kinetic energy

    • This is because the speed is changing

Worked Example

Calculate the kinetic energy stored in a vehicle of mass 1200 kg moving at a speed of 27 m/s.

Answer:

Step 1: List the known quantities

  • Mass of the vehicle, m = 1200 kg

  • Speed of the vehicle, v = 27 m/s

Step 2: Write down the equation for kinetic energy

Ek = ½ mv2

Step 3: Calculate the kinetic energy

Ek = ½ × 1200 × (27)2 = 437 400 J

Step 4: Round the final answer to 2 significant figures

Ek = 440 000 J

Examiner Tips and Tricks

Writing out your list of known quantities, and labelling the quantity you need to calculate, is really good exam technique. It helps you determine the correct equation to use, and sometimes examiners award credit for showing this working.

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Area Under Velocity-Time GraphsNext:Contact & Non-Contact Forces
    Author
    Reviewer
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.