Force & Pressure (OCR GCSE Physics A (Gateway)) : Revision Note
Pressure in a Fluid
A fluid is either a liquid or a gas
When an object is immersed in a fluid, the fluid exerts a pressure upon the object
This pressure is in addition to the pressure already exerted by the atmosphere
For example, an object at sea level (on the surface of the sea) experiences a pressure of 101 kPa due to the atmosphere
If this object is now immersed to a depth of 10 metres underwater, it experiences an extra pressure of 100 kPa due to the water
This means that the object will experience a total pressure of
101 kPa + 100 kPa = 201 kPa
This pressure arises due to both:
The water pressure
Atmospheric pressure
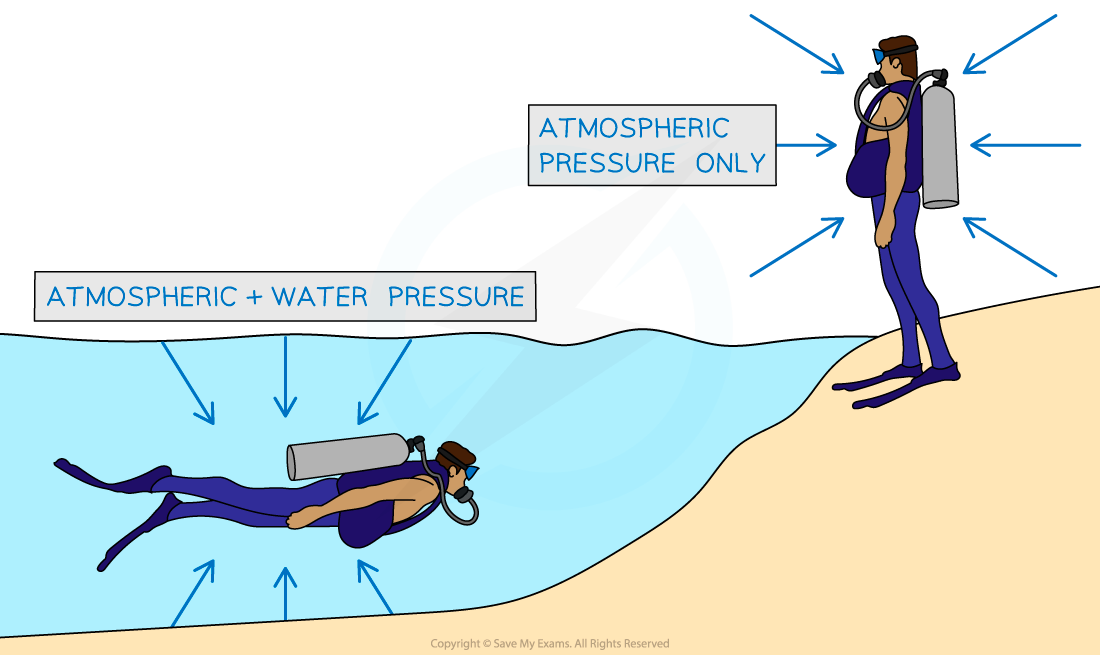
When an object is immersed in a fluid, it experiences pressure due to both the fluid and the atmosphere
The Force Exerted by a Fluid
When an object is immersed in a fluid, the fluid will exert pressure, squeezing the object
This pressure is exerted evenly across the whole surface of the fluid and in all directions
The pressure exerted on objects in fluids creates forces against surfaces
These forces act at 90 degrees (at right angles or 'normal') to the surface
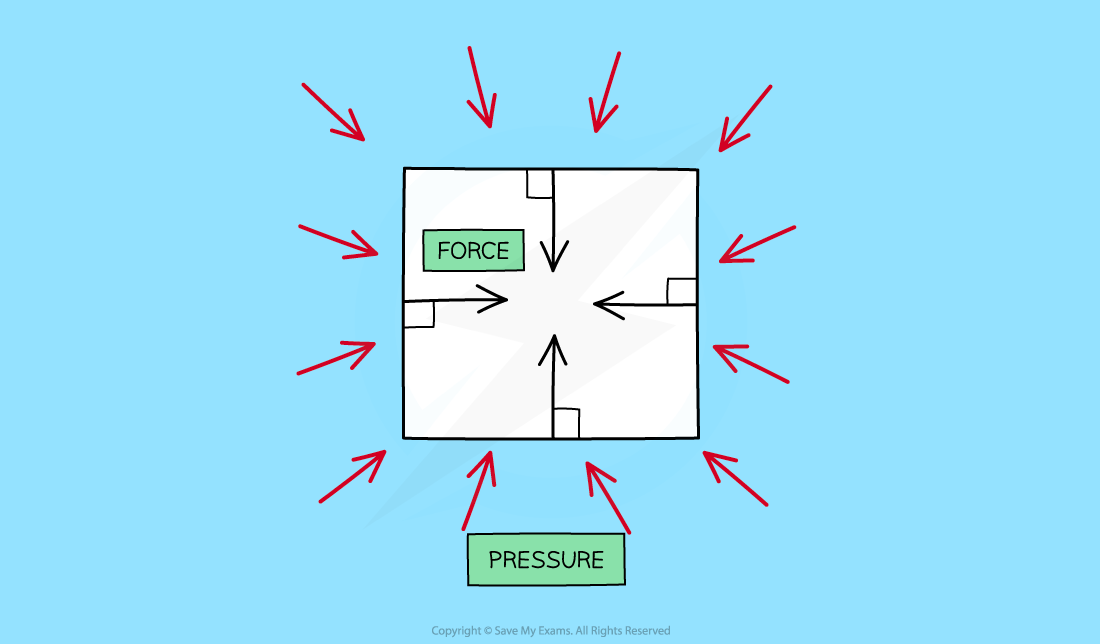
The pressure of a fluid on an object creates a force normal (at right angles) to the surface
Pressure & Depth
When an object is immersed in a liquid, the liquid will exert a pressure, squeezing the object
This pressure is exerted evenly across the whole surface of the liquid and in all directions
The greater the depth of the liquid, the greater the pressure
The greater the density of the liquid, the greater the pressure
In a liquid, the pressure at a point increases with the height of the column of liquid about that point
If there is more liquid above that point, then the pressure is more
This is because the pressure in a liquid is caused by the weight of the liquid pushing against objects immersed in the liquid
As the liquid becomes deeper, the amount of liquid (and hence the weight) increases which causes the pressure to increase
This is why, for example, the pressure increases with the depth of the ocean
The pressure on the seabed is far higher than that on the surface of the ocean
The weight of the liquid also depends on its density
A more dense liquid has a greater weight and therefore will exert a higher pressure
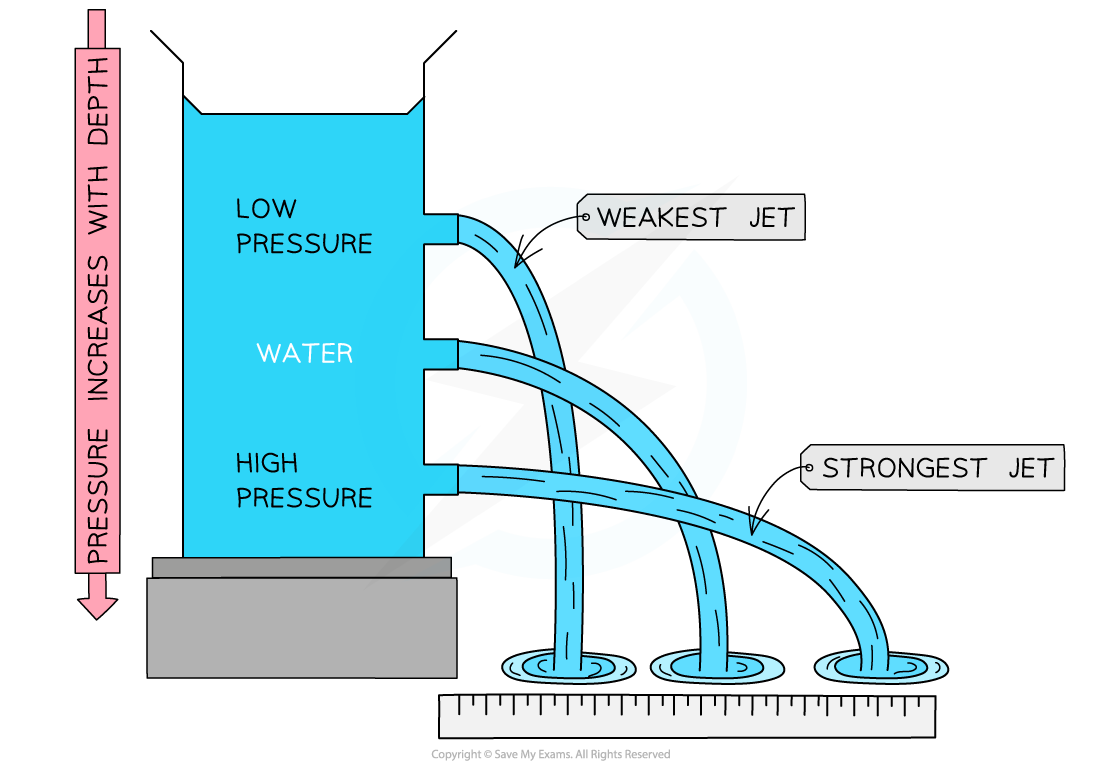
Pressure in a column of water increases with depth, shown by the strong and weak jet of water
In a column of water, the highest pressure would be at the bottom
If a hole is made at the bottom of the column, the water will pour out with a large force
If a hole was made at the top of the column, the water will pour out with a small force
This is because of the difference in pressure in the column caused by the weight of the water
Atmospheric Pressure
The Earth's atmosphere is a thin layer (relative to the size of the Earth) of air around it
It exerts a pressure of about 101 kPa at sea level

The Earth's atmosphere
The atmosphere extends more than 100 km into space and becomes less dense with increasing altitude (height above sea level)
This means that the pressure becomes less too
Atmospheric pressure various slightly from day to day, depending on the weather, and fine clear weather is usually associated with high pressure
The graph below shows how the pressure varies with altitude:
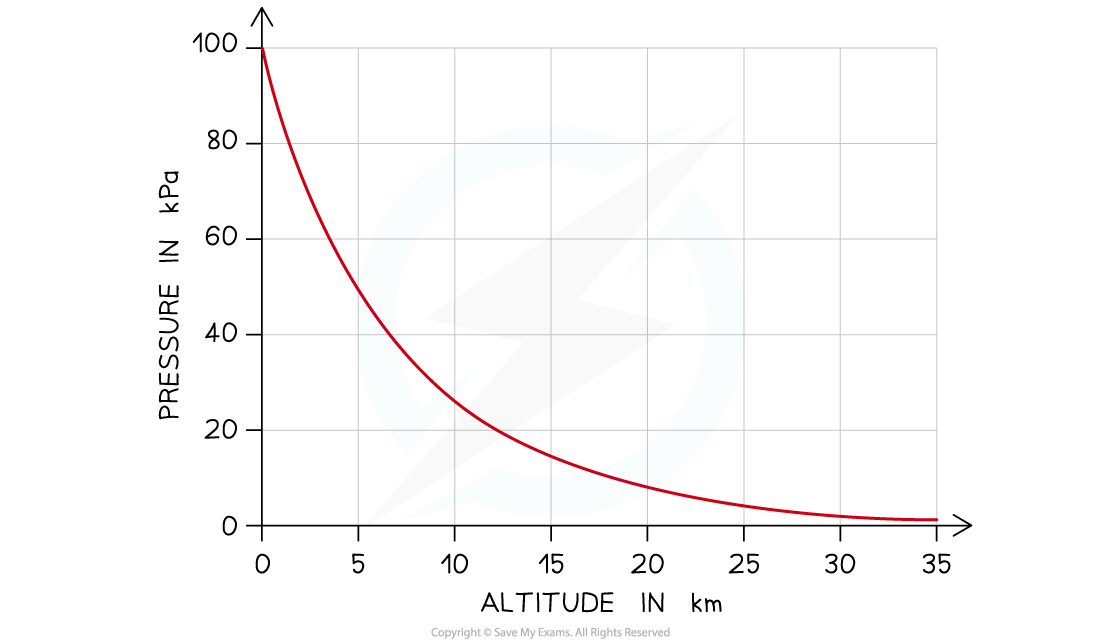
Graph of atmospheric pressure against altitude
Atmospheric pressure varies with height above a surface, for example, at sea level
This is due to air molecules colliding with a surface creating atmospheric pressure
These molecules create a force per area of the surface which creates the pressure
The number of air molecules (and so the weight of air) above a surface decreases as the height of the surface above ground level increases
This is also known as the density of the air
Therefore, as height increases, there is always less air above a surface than there is at a lower height and the atmospheric pressure decreases with an increase in height
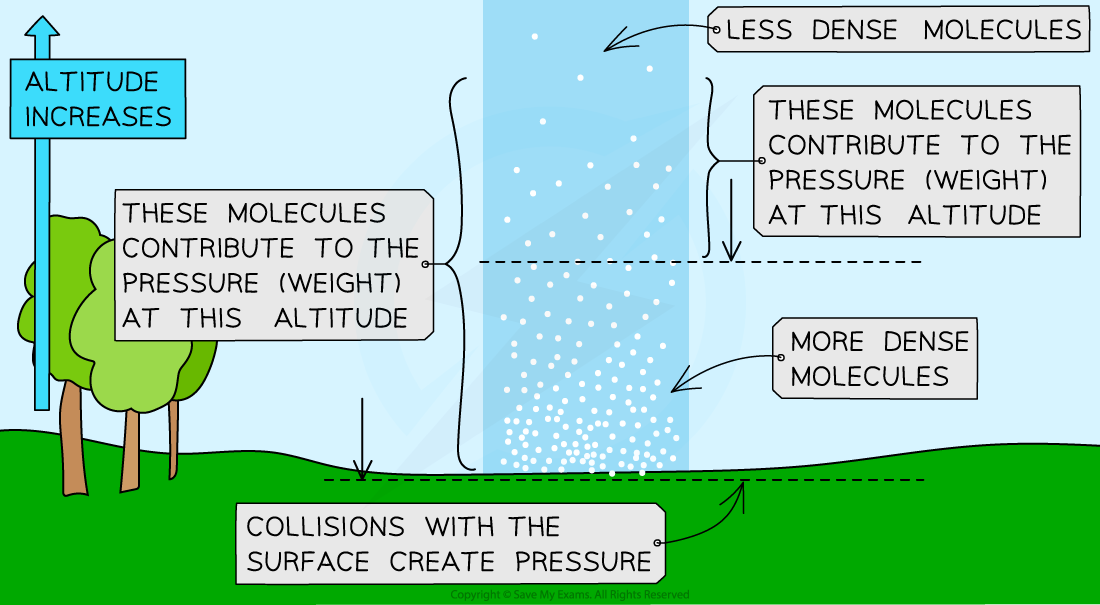
Atmospheric pressure decreases as the density of the molecules decreases
Calculating Pressure
Pressure in Solids
Pressure is defined as
The concentration of a force or the force per unit area
For example, when a drawing pin is pushed downwards:
It is pushed into the surface, rather than up towards the finger
This is because the sharp point is more concentrated (a small area) creating a larger pressure
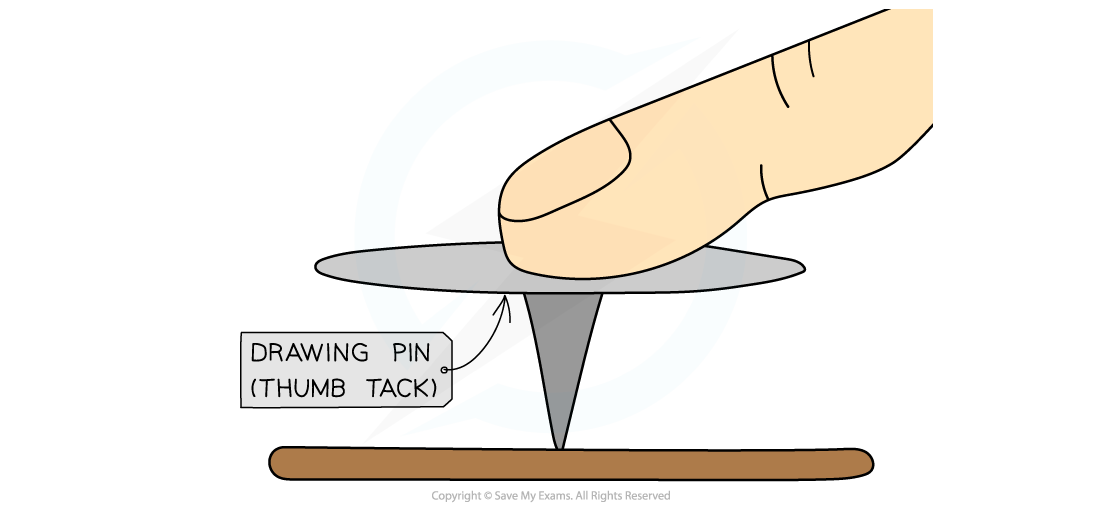
When you push a drawing pin, it goes into the surface (rather than your finger)
Example 1: Tractors
Tractors have large tyres
This spreads the weight (force) of the tractor over a large area
This reduces the pressure which prevents the heavy tractor from sinking into the mud
Example 2: Nails
Nails have sharp pointed ends with a very small area
This concentrates the force, creating a large pressure over a small area
This allows the nail to be hammered into a wall
Calculating Pressure between Solids
The pressure between solids can be calculated using the equation:
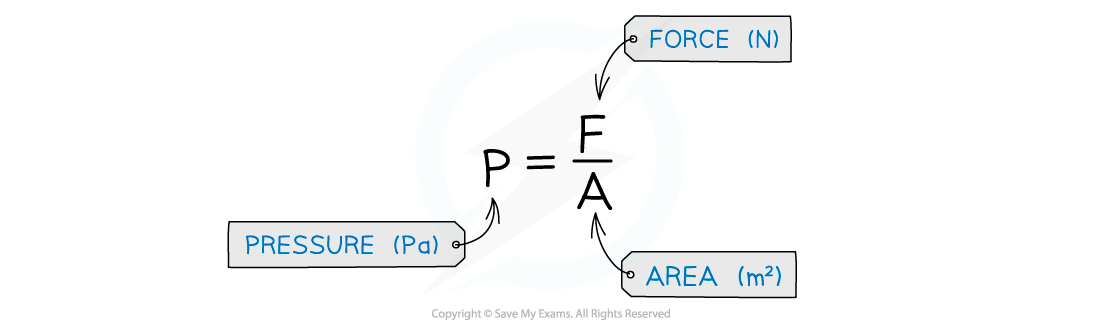
Pressure is measured in the units Pascals (Pa)
The area should always be the cross-sectional area of the object
This means the area where the force is at right angles to it
This equation can be rearranged with the help of a formula triangle:

Force, pressure, area formula triangle
This equation tells us that:
If a force is spread over a large area it will result in a small pressure
If it is spread over a small area it will result in a large pressure
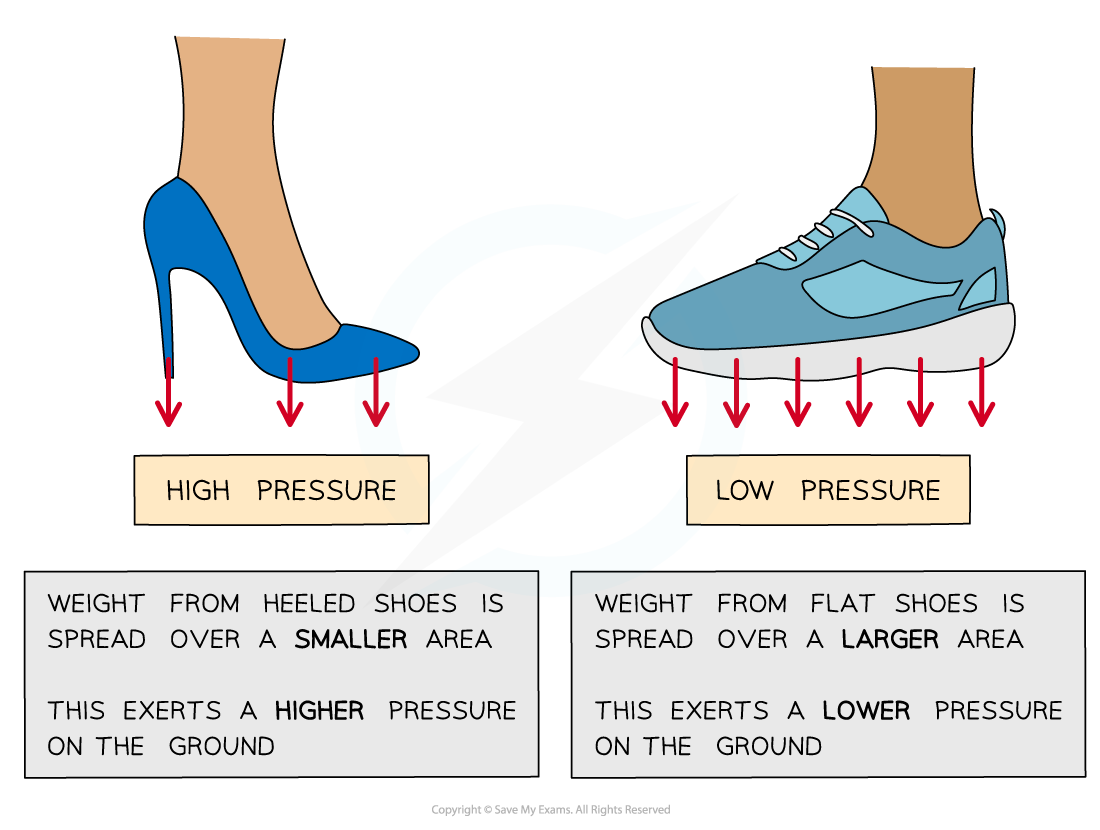
High heels produce a higher pressure on the ground because of their smaller area, compared to flat shoes
Worked Example
The diagram below shows the parts of the lifting machine used to move the platform up and down.
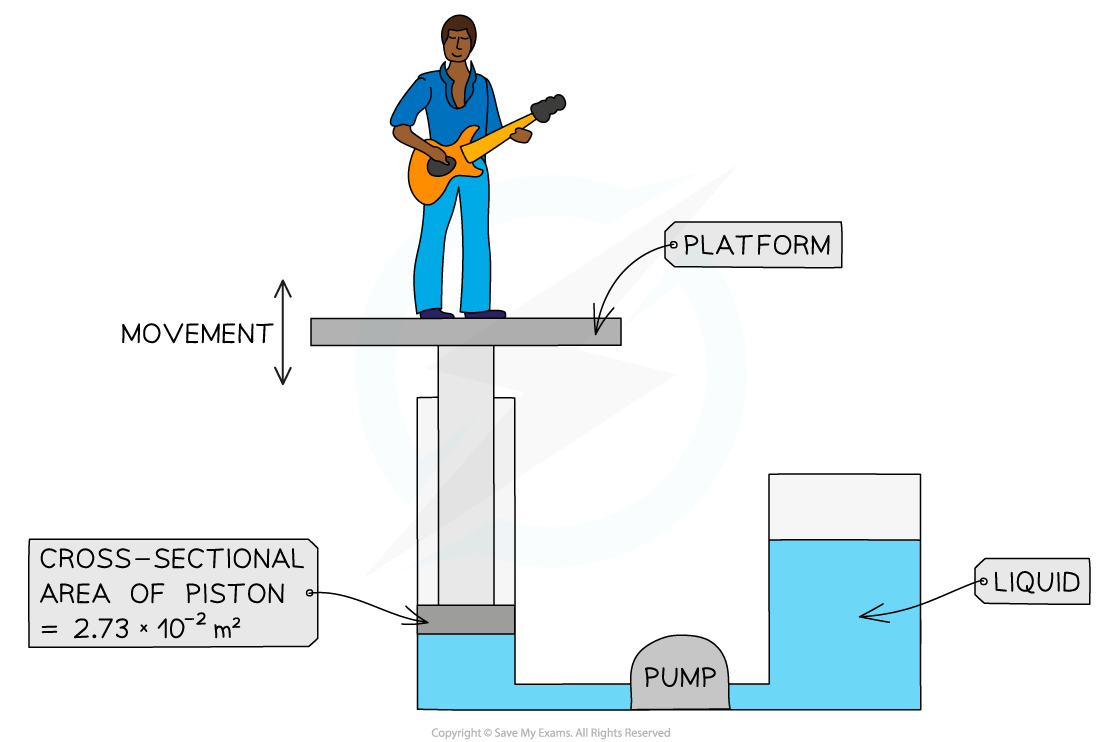
The pump creates pressure in the liquid of 5.28 × 105 Pa to move the platform upwards. Calculate the force that the liquid applies to the piston.
Answer:
Step 1: List the known quantities
Cross-sectional area = 2.73 × 10-2 m2
Pressure = 5.28 × 105 Pa
Step 2: Write down the relevant equation
Step 3: Rearrange for the force, F
F = p × A
Step 4: Substitute the values into the equation
F = (5.28 × 105) × (2.73 × 10-2) = 14 414.4
Step 5: Round to the appropriate number of significant figures and quote the correct unit
F = 14 400 N = 14.4 kN (3 s.f)
Calculating Pressure in a Fluid
The pressure due to a column of liquid can be calculated using the equation
p = h × ρ × g
Where:
p = pressure in pascals (Pa)
h = height of the column in metres (m)
ρ = density of the liquid in kilograms per metre cubed (kg/m3)
g = gravitational field strength on Earth in newtons per kilogram (N/kg)
The force from the pressure is exerted evenly across the whole surface of an object in a liquid, and in all directions
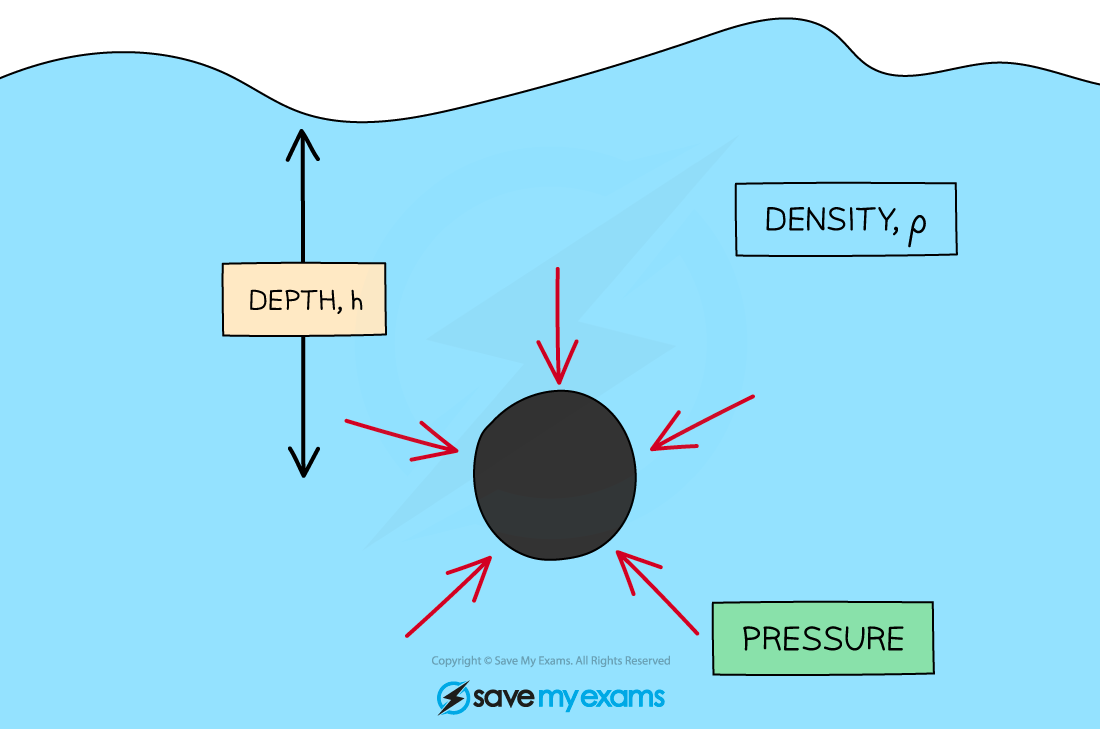
The force from the pressure of objects in a liquid is exerted evenly across its whole surface
The pressure is more accurately the difference in pressure at different depths h in a liquid, since the pressure changes with the depth
Worked Example
Calculate the depth of water in a swimming pool where a pressure of 20 kPa is exerted. The density of water is 1000 kg/m3 and the gravitational field strength on Earth is 9.8 N/kg.
Answer:
Step 1: List the known quantities
Pressure, p = 20 kPa
Density of Water , ρ =1000kg/m3
Gravitational field strength, g=9.8 N/kg
Step 2: List the relevant equation
p = hρg
Step 3: Rearrange for the height, h
Step 4: Convert any units
20 kPa=20 000 Pa
Step 5: Substitute in the values
Examiner Tips and Tricks
Look out for the units for the force when calculating pressure between solids! Large pressures produce large forces - this is sometimes in kN! (1 kN = 1000 N)
This pressure equation for pressure in liquids will be given on your formula sheet, however, make sure you are comfortable with rearranging it for the variable required in the question!

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

