KE, GPE & EPE (OCR GCSE Physics A (Gateway)): Revision Note

KE, GPE & EPE

Kinetic Energy

• Energy in an object's kinetic store is defined as:

  The amount of energy an object has as a result of its mass and speed

• This means that any object in motion has energy in its kinetic energy store

• Kinetic energy can be calculated using the equation:

$E=\frac{1}{2}m{v}^2$

• Where:

  • E = kinetic energy in joules (J)

  • m = mass of the object in kilograms (kg)

  • v = speed of the object in metres per second (m/s)

Gravitational Potential Energy

• Energy in the gravitational potential store of an object is defined as:

  The energy an object has due to its height in a gravitational field

• This means:

  • If an object is lifted up, energy will be transferred to its gravitational store 

  • If an object falls, energy will be transferred away from its gravitational store 

• The gravitational potential energy of an object can be calculated using the equation:

$E=mgh$

• Where:

  • E = change in gravitational potential energy, in joules (J)

  • m = mass, in kilograms (kg)

  • g = gravitational field strength in newtons per kilogram (N/kg)

  • h = change in height in metres (m)

Energy is transferred to the mass's gravitational store as it is lifted above the ground

Elastic Potential Energy

• Energy in the elastic potential store of an object is defined as:

  The energy stored in an elastic object when work is done on the object

• This means that any object that can change shape by stretching, bending or compressing (eg. springs, rubber bands)

  • When a spring is stretched (or compressed), work is done on the spring which results in energy being transferred to the elastic potential store of the spring

  • When the spring is released, energy is transferred away from its elastic potential store

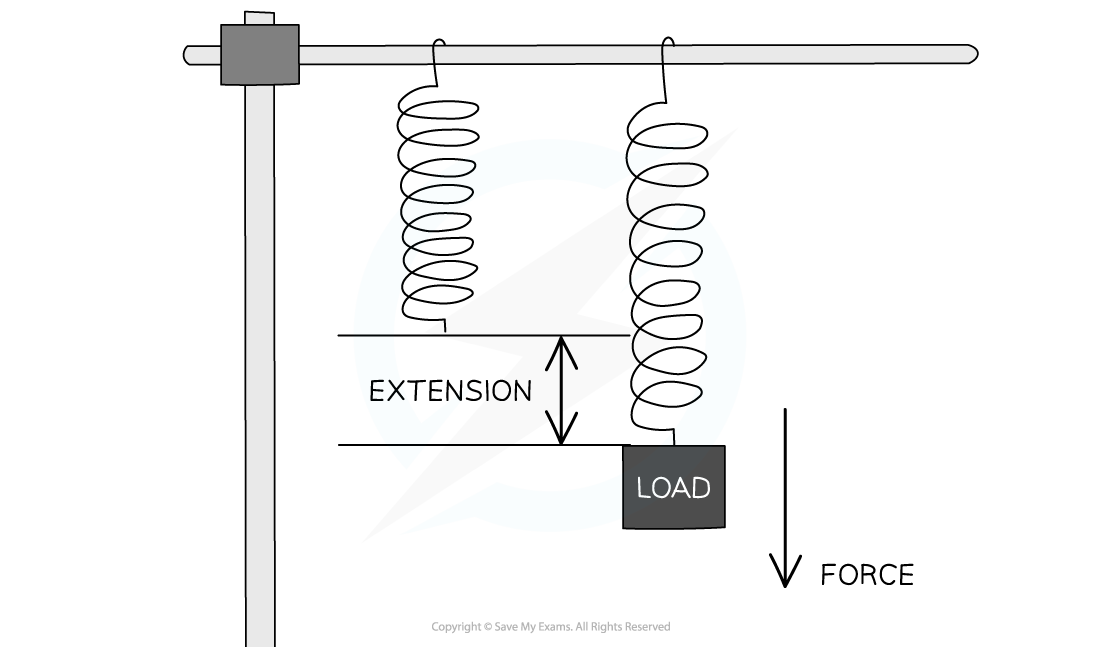
How to determine the extension, e, of a stretched spring

• The amount of elastic potential energy stored in a stretched spring can be calculated using the equation:

$E_e=\frac{1}{2}k{x}^2$

• Where:

  • E_e = elastic potential energy in joules (J)

  • k = spring constant in newtons per metre (N/m)

  • x = extension in metres (m)

• The above equation assumes that the spring has not been stretched beyond its limit of proportionality

The spring on the right has been stretched beyond the limit of proportionality

Energy Transfers in a Vertical Spring

• When a vertical spring is extended and contracted, energy is transferred

• Although the total energy of the spring system will remain constant, energy will be transferred between

  • The elastic potential energy store

  • The kinetic energy store

  • The gravitational potential energy store

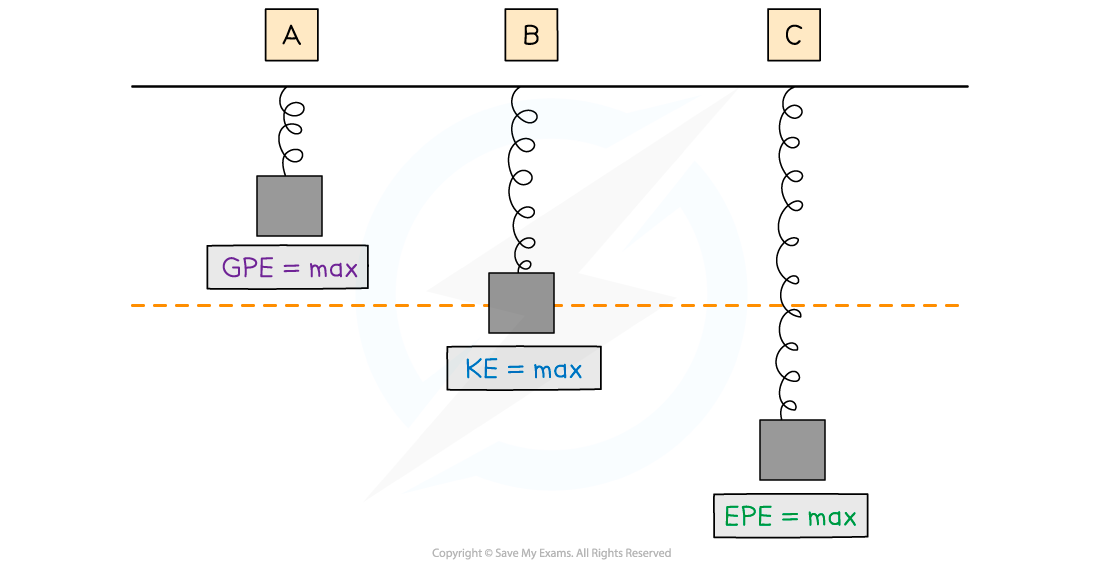
Energy transfers when a spring oscillates

• At position A:

  • The spring has some energy in its elastic potential store since it is slightly compressed

  • The spring has zero energy in its kinetic store since it is stationary

  • The amount of energy in the gravitational potential store of the spring is at a maximum because the mass is at its highest point

• At position B:

  • The spring has some energy in its elastic potential store since it is slightly stretched

  • The amount of energy in its kinetic store is at a maximum as it passes through its resting position at its maximum speed

  • The spring has some energy in its gravitational potential store since the mass is at its midway point in height

• At position C:

  • The amount of energy in the elastic potential store of the spring is at its maximum because it is at its maximum extension

  • The spring has zero energy in its kinetic store since it is stationary

  • The amount of energy in the gravitational potential store GPE is at a minimum because it is at its lowest point in the oscillation