KE, GPE & EPE

Kinetic Energy

Energy in an object's kinetic store is defined as:

The amount of energy an object has as a result of its mass and speed

This means that any object in motion has energy in its kinetic energy store

1-7-2-kinetic-energy-cie-igcse-23-rn

Kinetic energy can be calculated using the equation:

$E = \frac{1}{2} m v^{2}$

Where:
- E = kinetic energy in joules (J)
- m = mass of the object in kilograms (kg)
- v = speed of the object in metres per second (m/s)

Gravitational Potential Energy

Energy in the gravitational potential store of an object is defined as:

The energy an object has due to its height in a gravitational field

This means:
- If an object is lifted up, energy will be transferred to its gravitational store
- If an object falls, energy will be transferred away from its gravitational store

The gravitational potential energy of an object can be calculated using the equation:

$E = m g h$

Where:
- E = change in gravitational potential energy, in joules (J)
- m = mass, in kilograms (kg)
- g = gravitational field strength in newtons per kilogram (N/kg)
- h = change in height in metres (m)

1-7-3-gravitational-potential-energy-cie-igcse-23-rn

Energy is transferred to the mass's gravitational store as it is lifted above the ground

Elastic Potential Energy

Energy in the elastic potential store of an object is defined as:

The energy stored in an elastic object when work is done on the object

This means that any object that can change shape by stretching, bending or compressing (eg. springs, rubber bands)
- When a spring is stretched (or compressed), work is done on the spring which results in energy being transferred to the elastic potential store of the spring
- When the spring is released, energy is transferred away from its elastic potential store

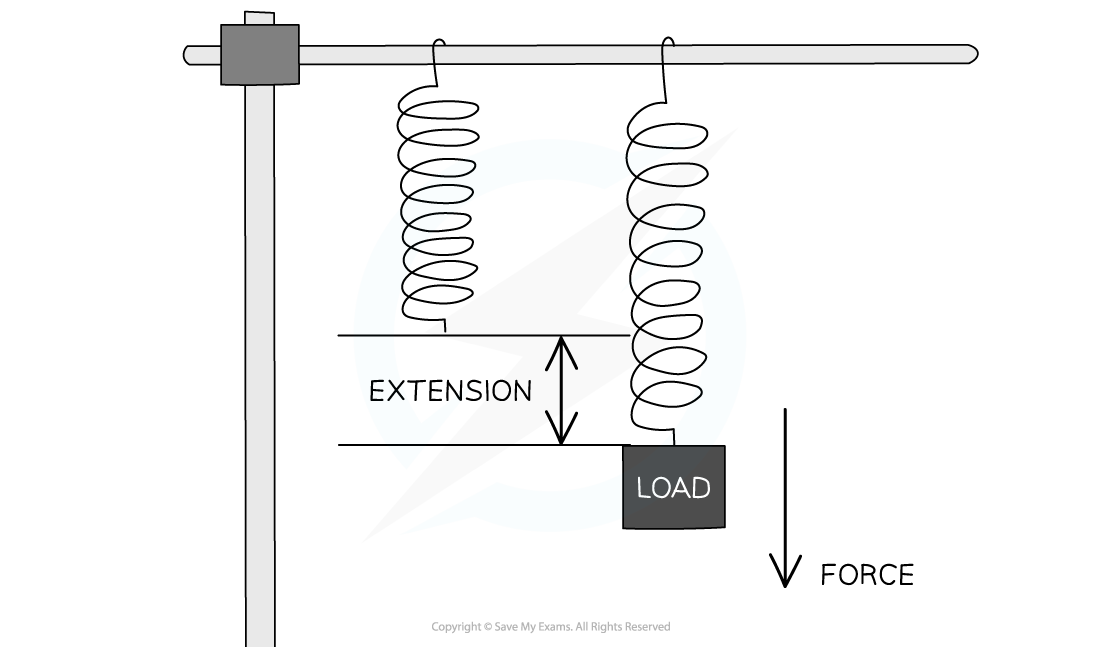
Load extension and force, downloadable AS & A Level Physics revision notes

How to determine the extension, e, of a stretched spring

The amount of elastic potential energy stored in a stretched spring can be calculated using the equation:

$E_{e} = \frac{1}{2} k x^{2}$

Where:
- E_e = elastic potential energy in joules (J)
- k = spring constant in newtons per metre (N/m)
- x = extension in metres (m)

The above equation assumes that the spring has not been stretched beyond its limit of proportionality

Elastic-limit, IGCSE & GCSE Physics revision notes

The spring on the right has been stretched beyond the limit of proportionality

Energy Transfers in a Vertical Spring

When a vertical spring is extended and contracted, energy is transferred
Although the total energy of the spring system will remain constant, energy will be transferred between
- The elastic potential energy store
- The kinetic energy store
- The gravitational potential energy store

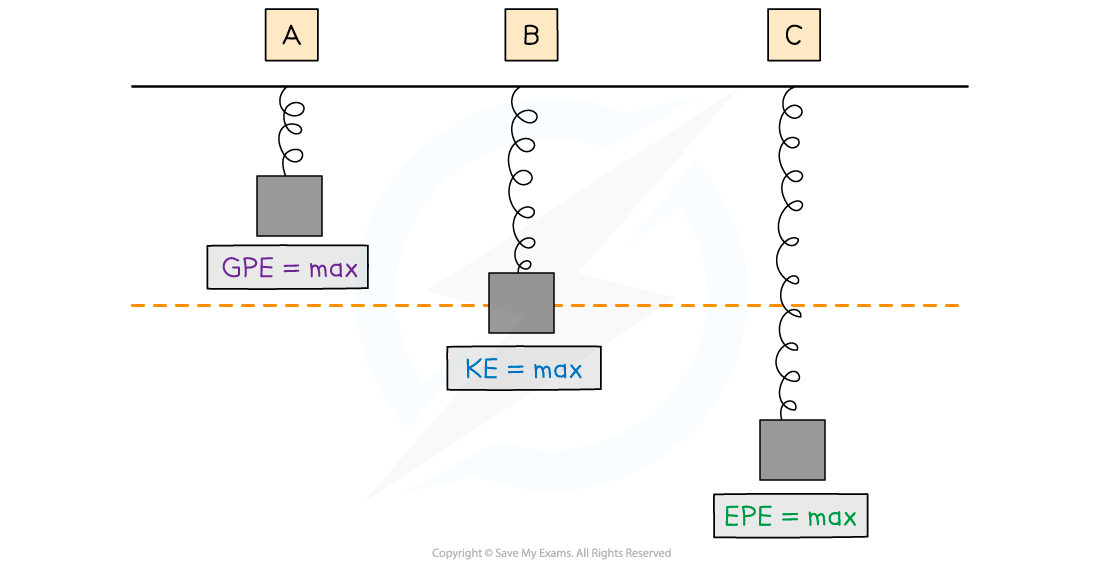
Change in Spring Energy, downloadable AS & A Level Physics revision notes

Energy transfers when a spring oscillates

At position A:
- The spring has some energy in its elastic potential store since it is slightly compressed
- The spring has zero energy in its kinetic store since it is stationary
- The amount of energy in the gravitational potential store of the spring is at a maximum because the mass is at its highest point
At position B:
- The spring has some energy in its elastic potential store since it is slightly stretched
- The amount of energy in its kinetic store is at a maximum as it passes through its resting position at its maximum speed
- The spring has some energy in its gravitational potential store since the mass is at its midway point in height

At position C:
- The amount of energy in the elastic potential store of the spring is at its maximum because it is at its maximum extension
- The spring has zero energy in its kinetic store since it is stationary
- The amount of energy in the gravitational potential store GPE is at a minimum because it is at its lowest point in the oscillation

Worked example

The diagram below shows a student before and after a bungee jump. The bungee cord has an unstretched length of 30.0 m. KE GPE EPE Worked Example, downloadable AS & A Level Physics revision notes

The mass of the student is 60.0 kg. The gravitational field strength is 9.8 N / kg.

Calculate:

a) The change in gravitational potential energy of the student at 30.0 m

b) The maximum change in the gravitational potential energy of the student

c) The speed of the student after falling 30.0 m if 90% of the energy in the student's gravitational potential store is transferred to the student's kinetic store

d) The spring constant of the bungee cord if all the energy in the gravitational potential store of the student is transferred to the elastic potential store of the bungee cord

Part (a)

Step 1: List the known quantities

- - Mass of the student, m = 60.0 kg
  - Gravitational field strength, g = 10 N/kg
  - Change in height, h = 30.0 m

Step 2: Write out the equation for gravitational potential energy

$E = m g h$

Step 3: Calculate the change in gravitational potential energy

$E = 60 \times 10 \times 30$

$E = 18 000 J$

Part (b)

Step 1: List the known quantities

- - Mass of the student, m = 60.0 kg
  - Gravitational field strength, g = 10 N/kg
  - Maximum change in height, h = 75.0 m

Step 2: Calculate the maximum change in gravitational potential energy

$E_{m a x} = m g h_{m a x}$

$E_{m a x} = 60 \times 10 \times 75$

$E_{m a x} = 45 000 J$

Part (c)

Step 1: List the known quantities

- - Mass of the student, m = 60.0 kg
  - $E$ at 30.0 m = 18 000 J

Step 2: Determine 90% of the $E$ at 30.0 m

$E = 0.9 \times 18 000$

$E = 16 200 J$

Step 3: Write out the equation for KE

$E = \frac{1}{2} m v^{2}$

Step 4: Rearrange to make speed the subject

- - Multiply both sides by 2:

$m v^{2} = 2 E$

- - Divide both sides by m:

$v^{2} = \frac{2 E}{m}$

- - Take the square root of both sides:

$v = \sqrt{\frac{2 E}{m}}$

Step 5: Calculate the speed

$v = \sqrt{\frac{2 \times 16 200}{60}}$

$v = 23.2 m / s$

Part (d)

Step 1: List the known quantities

- - $E_{m a x}$ = 45 000 J
  - $E_{e}$ at 75.0 m = $E_{e m a x}$
- Step 2: Determine the extension of the bungee cord

$e = 75.0 - 30.0$

$e = 45.0 m$

Step 3: Write out the equation for elastic potential energy

$E_{e} = \frac{1}{2} k x^{2}$

Step 3: Rearrange to make spring constant, k, the subject

- - Multiply both sides by 2:

$k x^{2} = 2 E_{e}$

- - Divide both sides by $x^{2}$ :

$k = \frac{2 E_{e}}{x^{2}}$

Step 4: Calculate the spring constant

$k = \frac{2 \times 45 000}{45^{2}}$

$k = 44.4 N / m$

Examiner Tip

If a question asks you to "state" a value, you do not need to carry out a calculation: The answer will almost certainly be a number either from a previous answer or which was given somewhere in the question.

For example, if you have just calculated the gravitational potential energy of an object and are then asked to state the kinetic energy a moment later, the answers are very likely to be the same.

KE, GPE & EPE (OCR Gateway GCSE Physics)

Revision Note

KE, GPE & EPE

Kinetic Energy

Gravitational Potential Energy

Elastic Potential Energy

Energy Transfers in a Vertical Spring

Worked example

Examiner Tip

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Leander