Resistors in Series & Parallel (OCR GCSE Physics A (Gateway)): Revision Note
Exam code: J249
Resistors in Series & Parallel
Resistors in Series
When two or more resistors are connected in series, the total (or combined) resistance is equal to the sum of their individual resistances
For example, for three resistors of resistance R1, R2 and R3, the total resistance can be calculated using:

Where R is the total resistance, in Ohms (Ω)
Increasing the number of resistors increases the overall resistance, as the charge now has more resistors to pass through
The total voltage is also the sum of the voltages across each of the individual resistors
In a series circuit, the voltage of the power supply is shared between all components

Three resistors connected in series. The total voltage is the sum of the individual voltages, and the total resistance is the sum of the three individual resistances
Resistors in Parallel
When two or more resistors are connected in parallel, the total (or net / combined) resistance decreases
In the below circuit, the combined resistance of the resistors R1 and R2 is less than if they were connected in series

Two resistors connected in parallel. The total resistance is less than if they were connected in series
This happens because each resistor creates an extra path along which the charge can flow
This allows more charge to flow overall
This leads to a smaller overall resistance
The advantages of this kind of circuit are:
The components can be individually controlled, using their own switches
If one component stops working the others will continue to function
Worked Example
The combined resistance R in the following series circuit is 60 Ω.What is the resistance value of R2?
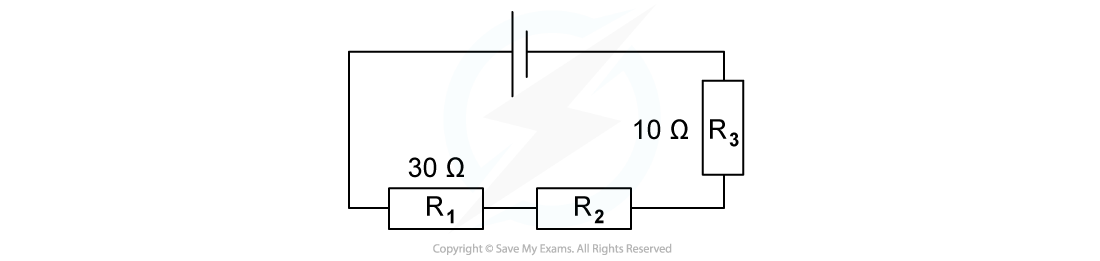
A. 100 Ω B. 30 Ω C. 20 Ω D. 40 Ω
Answer: C
Step 1: Write down the equation for the combined resistance in series
R = R1 + R2 + R3
Step 2: Substitute the values for total resistance R and the other resistors
60 Ω = 30 Ω + R2 + 10 Ω
Step 3: Rearrange for R2
R2 = 60 Ω – 30 Ω – 10 Ω = 20 Ω
Worked Example
Dennis sets up a series circuit as shown below.
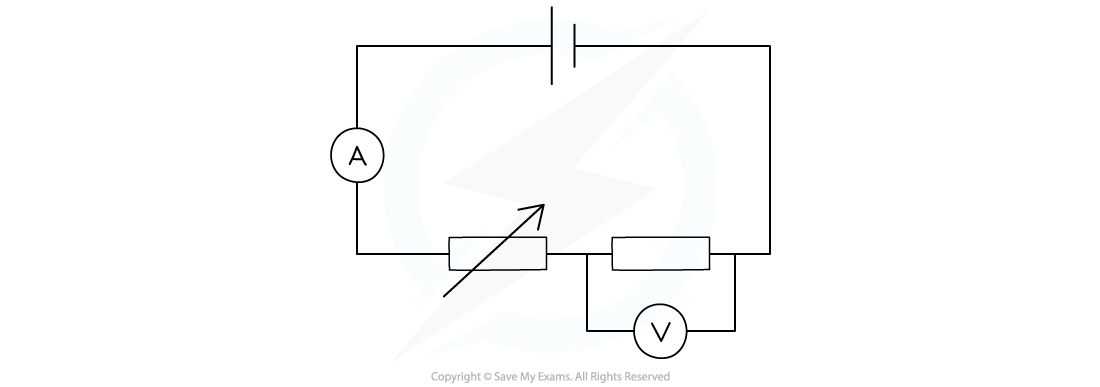
The cell supplies a current of 2 A to the circuit, and the fixed resistor has a resistance of 4 Ω.
(a) How much current flows through the fixed resistor?
(b) What is the reading on the voltmeter?
Answer:
Part (a)
Step 1: Recall that current is conserved in a series circuit
Since current is conserved in a series circuit, it is the same size if measured anywhere in the series loop
This means that since the cell supplies 2 A to the circuit, current is 2 A everywhere
Therefore, 2 A flows through the fixed resistor
Part (b)
Step 1: List the known quantities
Current I = 2 A
Resistance R = 4 Ω
Step 2: State the equation linking potential difference, resistance and current
The equation linking potential difference, resistance and current is:
V = IR
Step 3: Substitute the known values into the equation and calculate the potential difference
V = 2 × 4 = 8 V
Therefore, the voltmeter reads 8 V across the fixed resistor
Examiner Tips and Tricks
Circuit questions can be confusing. Remember to label any voltages, currents or resistances on the circuit to help with the calculations and most of all, remember how voltage, current and resistance differs between a series and parallel circuit (as you may get a question on a combination of both circuits!)

Unlock more, it's free!
Did this page help you?