Area Under Velocity-Time Graphs (OCR Gateway GCSE Physics)

• The area under a velocity-time graph represents the displacement (or distance travelled) by an object

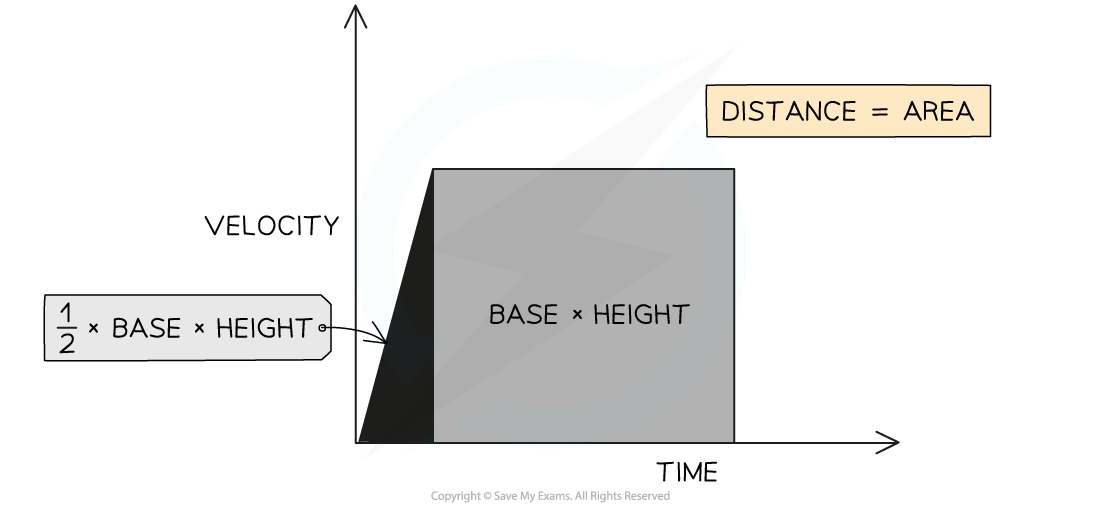
The displacement, or distance travelled, is represented by the area beneath the graph

• If the area beneath the graph forms a triangle (i.e. the object is accelerating or decelerating), then the area can be determined by using the following formula:

Area = ½ × Base × Height

• If the area beneath the graph forms a rectangle (i.e. the object is moving at a constant velocity), then the area can be determined by using the following formula:

Area = Base × Height

Determining Distance from a Velocity-Time Graph

• Enclosed areas under velocity-time graphs represent total displacement (or total distance travelled)

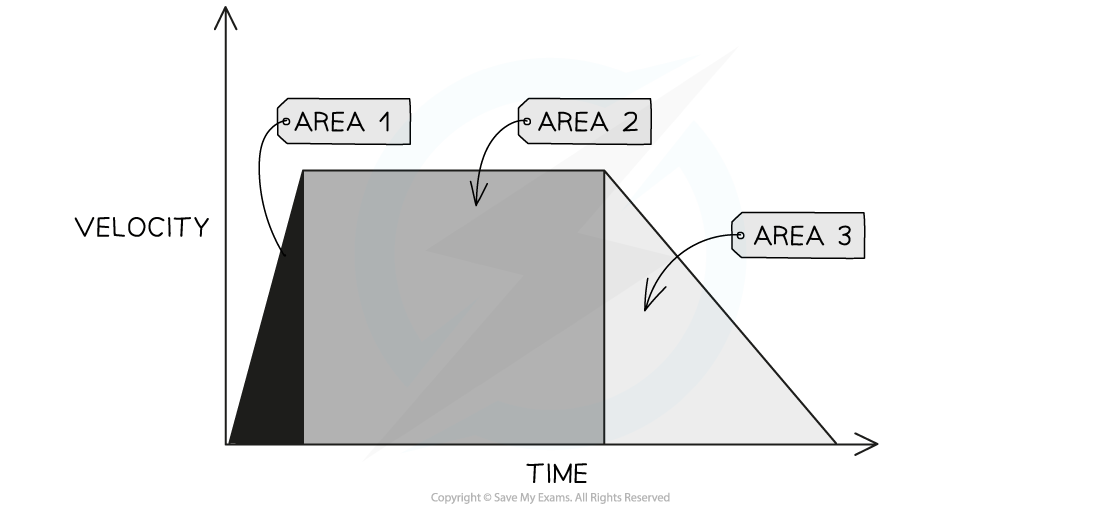
Three enclosed areas (two triangles and one rectangle) under this velocity-time graph represents the total distance travelled

• If an object moves with constant acceleration, its velocity-time graph will comprise of straight lines
  • In this case, calculate the distance travelled by working out the area of enclosed rectangles and triangles as in the image above

Step 1: Recall that the area under a velocity-time graph represents the distance travelled

• • In order to calculate the total distance travelled, the total area underneath the line must be determined

Step 2: Identify each enclosed area

• • In this example, there are five enclosed areas under the line
  • These can be labelled as areas 1, 2, 3, 4 and 5, as shown in the image below:

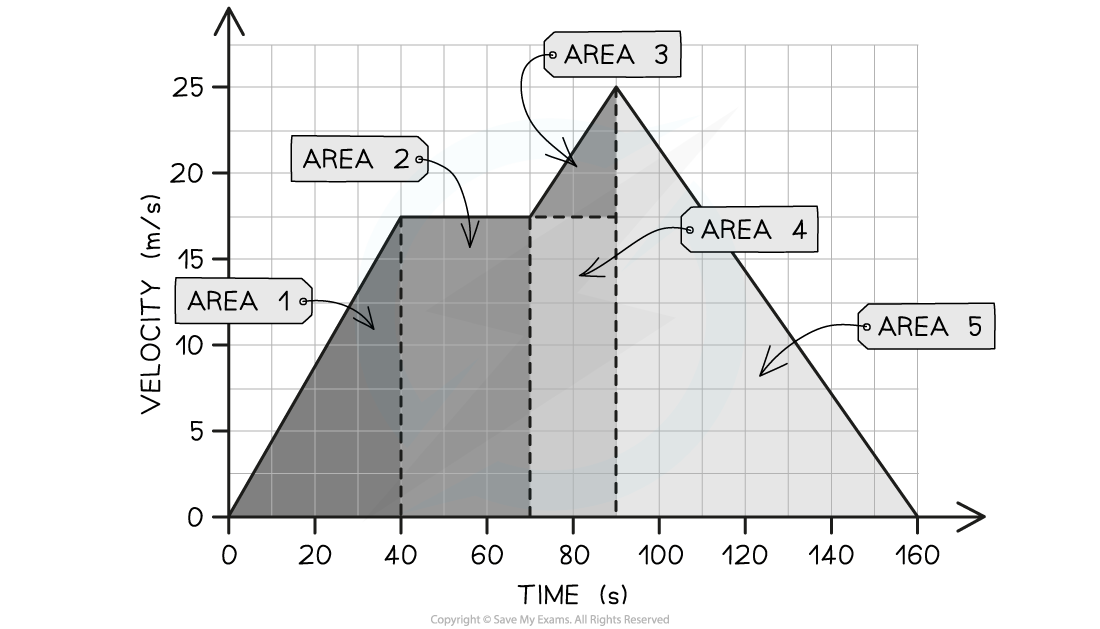
Step 3: Calculate the area of each enclosed shape under the line

• • Area 1 = area of a triangle = ½ × base × height = ½ × 40 × 17.5 = 350 m
  • Area 2 = area of a rectangle = base × height = 30 × 17.5 = 525 m
  • Area 3 = area of a triangle = ½ × base × height = ½ × 20 × 7.5 = 75 m
  • Area 4 = area of a rectangle = base × height = 20 × 17.5 = 350 m
  • Area 5 = area of a triangle = ½ × base × height = ½ × 70 × 25 = 875 m

Step 4: Calculate the total distance travelled by finding the total area under the line

• • Add up each of the five areas enclosed:

total distance = 350 + 525 + 75 + 350 + 875

total distance = 2175 m