GCSEPhysicsEdexcelExam Questions9. Forces & their Effects9.2 Moments

Moments (Edexcel GCSE Physics)

Exam Questions

1 hour9 questions
Easy
Medium
Hard
1a
Sme Calculator1 mark

State the equation for the moment of a force.

How did you do?

1b
Sme Calculator2 marks
Figure 1 shows a rod rotating anti-clockwise around an axle.
 
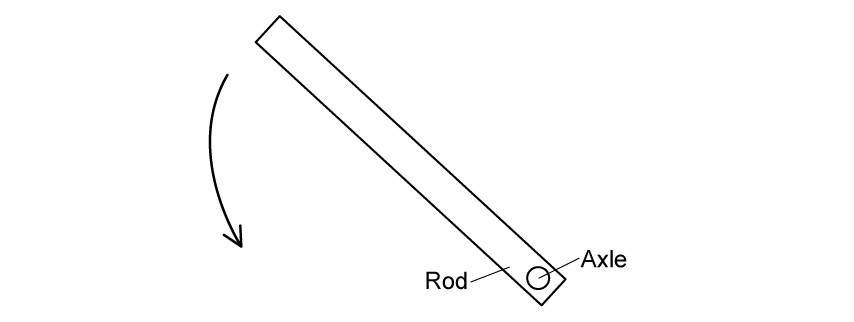
9-2-e-1b-moments-rod-rotating
Figure 1 
 
Sketch an arrow to show the force that will cause the biggest rotation. 

How did you do?

1c
Sme Calculator2 marks

Figure 2 now shows the rod with the axle in the middle instead.

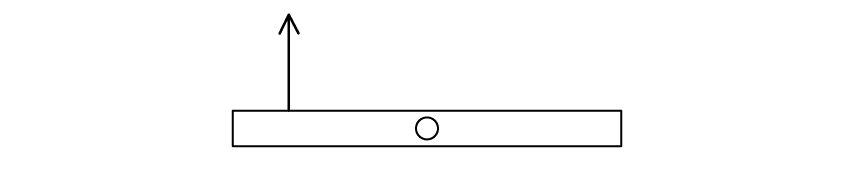
9-2-e-1c-moments-equilibrium
Figure 2
 

Draw an arrow on the rod that represents the force needed to keep the rod in equilibrium.

How did you do?

1d
Sme Calculator3 marks
The length of the rod in Figure 1 is 12 cm. The maximum moment for a force F that can be produced is 3.6 N m.

 

Calculate F.

How did you do?

Did this page help you?

2a
Sme Calculator1 mark

State the principle of moments.

How did you do?

2b
Sme Calculator3 marks

Figure 1 shows a force of 500 N acting at the end of a plank of wood. The force acts at right angles to the plank and at 4.1 m away from a pivot.

9-2-e-2b-principle-of-moments-2

Figure 1

 

Calculate the moment of the 500 N force about the pivot.

 

State the unit of the moment of the force.

 

Use the equation moment of a force = force × distance at right angles to the direction of the force

How did you do?

2c
Sme Calculator3 marks
When the box on the left side of the plank of wood is replaced with one with a weight of 350 N, the plank remains in equilibrium.
 
 

Calculate the distance of the centre of the box from the pivot.

How did you do?

2d
Sme Calculator2 marks
Explain what would happen if the 500 N force moved closer to the pivot. 
 

How did you do?

Did this page help you?

3a
Sme Calculator1 mark

Gears are used to multiply the effect of turning forces using moments.

Figure 1 shows two gears.
9-2-e-3a-gears-a-and-b
Figure 1

Gear B rotates clockwise.

State the direction of gear A.

How did you do?

3b
Sme Calculator1 mark

Gear A has 10 teeth.

Gear B has 50 teeth.

State how many revolutions gear A makes after 1 revolution of gear B.

How did you do?

3c
Sme Calculator1 mark

Figure 2 shows two gears, B and C.

9-2-e-3c-gear-b-and-c
Figure 2

Gear B can rotate on a fixed axle.

Gear C can move up and down.

The distance between each of the teeth on gear B and on gear C is 3 mm.

Gear B moves through one complete revolution anti-clockwise.

State the direction of gear C during this motion.

How did you do?

3d
Sme Calculator1 mark

After 1 complete revolution of B, determine the distance moved by gear C.

How did you do?

Did this page help you?

1a1 mark

A student investigates moments of forces.

Figure 14 shows the apparatus used.

fig-14-paper2h-oct2021-edexcel-gcse-physics

Figure 14

The pivot is under the centre of the rod.
A magnet is fixed to one end of the rod.
A piece of modelling clay is fixed to the other end of the rod.
The system is in equilibrium.

State the relationship between the moment of the weight of the magnet and the moment of the weight of the piece of modelling clay about the pivot.

How did you do?

1b3 marks

The student fixes a coil to the bench under the magnet as shown in Figure 15.

fig-15-paper2h-oct2021-edexcel-gcse-physics

Figure 15

The coil of wire is connected to a d.c. power supply so that there is a current in the coil.

To bring the system back into equilibrium, the student hangs a 0.050 N weight on the rod, 8.4 cm away from the pivot, as shown in Figure 15.

Calculate the size of the force between the magnet and the coil.

force = .............................................................. N

How did you do?

1c4 marks

Describe how the student could develop the investigation to determine if the size of the force between the magnet and the coil is directly proportional to the size of the current in the coil.

How did you do?

1d2 marks

The student reverses the direction of the current in the coil.
Describe how the student can bring the system back into equilibrium without making any changes to the magnet.

How did you do?

Did this page help you?

2a1 mark
Figure 19 shows four forces, P, Q, R and S, acting on a rod.
The rod can rotate around an axle.


fig-19-paper2f-june2019-edexcel-gcse-physics
Figure 19

Which force will make the rod rotate about the axle?

  ☐ A P
  ☐ B Q
  ☐ C R
  ☐ D S

How did you do?

2b5 marks

Figure 20 shows a person trying to lift a large rock using a metal bar.

fig-20-paper2f-june2019-edexcel-gcse-physics
Figure 20

The rock weighs 1800N.
The person can only produce a downwards force of 600N.
The person cannot lift the rock.

i)
Explain, using calculations, why the person cannot lift the rock.
[3]

ii)
Explain one change to the arrangement that will make it possible for this person to lift the rock.
[2]

How did you do?

2c5 marks
Figure 21 shows a bicycle.

pMOWhyLf_fig-21-paper2f-june2019-edexcel-gcse-physics

Figure 21

i)
The rider uses the pedals to make the large gear wheel turn.

The large gear wheel moves the chain. The chain turns the small gear wheel.

The large gear wheel has 48 teeth. The small gear wheel has 12 teeth.

The large gear wheel turns 2 times each second.

Calculate the number of times that the small gear wheel turns each second.

[2]

............................................... turns each second

ii)
Oil is applied to the wheel of a bicycle at the point shown in Figure 22.

fig-22-paper2f-june2019-edexcel-gcse-physics
Figure 22

Explain how the oil improves the efficiency of the bicycle.

[3]

How did you do?

Did this page help you?

3a2 marks

Physics Only

i)
Figure 9 shows two gears.

Gear Q moves clockwise as shown by the arrow.

fig-9-paper2f-june2018-edexcel-gcse-physics
Figure 9
Which of these describes how gear P moves?
[1]
  ☐ A anticlockwise, slower than gear Q
  ☐ B anticlockwise, faster than gear Q
  ☐ C clockwise, slower than gear Q
  ☐ D clockwise, faster than gear Q


ii)
Figure 10 shows the number of teeth on the gears.

Gear P has 24 teeth, gear Q has 16 teeth.

fig-10-paper2f-june2018-edexcel-gcse-physics
Figure 10

Which of these gives the ratio of the number of teeth on gear P to the number of teeth on gear Q?

[1]

  ☐ A 24 − 16
  ☐ B 16 + 24
  ☐ C 3 : 2
  ☐ D 2 : 3

How did you do?

3b7 marks

Figure 11 shows a lever used to lift a heavy load.

 

fig-11-paper2f-june2018-edexcel-gcse-physics

Figure 11

i)
The weight of the load is 650N.
The centre of the load is 0.75m from the pivot.

Calculate the moment of the load about the pivot.
State the unit.

Use the equation

     moment = force × distance from the pivot
[3]

moment = ............................................... unit ...............................................

ii)
State the principle of moments.

[1]

iii)
An effort of 160 N is applied to the end of the lever to balance the load in Figure 11.
Calculate the distance between the effort and the pivot.
[3]

distance = ............................................... m

How did you do?

Did this page help you?

1a3 marks

i)

Figure 6 shows two gears.

fig-6-paper2f-june2020-edexcel-gcse-physics

Figure 6

Gear R and gear S can rotate.
Gear R has 20 teeth.
Gear S has 60 teeth.
Gear S rotates through 2 complete revolutions.

Calculate how many complete revolutions gear R rotates by.

[2]

gear R has rotated through .............................................................. revolutions

ii)
Figure 7 shows two gears, S and T.

fig-7-paper2f-june2020-edexcel-gcse-physics

Figure 7

Gear S can rotate on a fixed axle.
Gear T can move up and down.
Gear S has 60 teeth.

The distance between each of the teeth on gear S and on gear T is 2 mm.
Gear S moves through one complete revolution in the direction shown.

Which of these describes the motion of gear T?

[1]

  ☐ A 60 mm up
  ☐ B 60 mm down
  ☐ C 120 mm up
  ☐ D 120 mm down

How did you do?

1b6 marks
i)
Figure 8 shows a force of 70 N turning a lever about point P.

fig-8-paper2f-june2020-edexcel-gcse-physics

Figure 8

Calculate the moment of the 70 N force about point P.
State the unit.
Use the equation

moment = force × distance normal to the direction of the force

[3]

moment = ..................... unit ...............

ii)
Figure 9 shows a worker using a wheelbarrow to move some sand.

fig-9-paper2f-june2020-edexcel-gcse-physics

Figure 9

The load is equal to the total weight of the sand and the wheelbarrow. The effort is the force that the worker applies to the wheelbarrow handles.

The worker applies just enough effort to lift the load.

Explain why the effort is smaller than the load.

[2]

iii)
Some sand falls down and sticks between the wheel and the axle.
 
State why it might be harder to push the wheelbarrow along when there is some sand between the wheel and the axle.

[1]

How did you do?

Did this page help you?

2a3 marks

Figure 10 shows an arrangement of gears.

Each gear turns around a fixed axle.

Wz2H1aNd_fig-10-paper2h-june2018-edexcel-gcse-physics

Figure 10

Gear P is turned through one complete revolution per second.

i)
Which of the following describes the motion of gear R?

      speed(revolutions per second) direction of rotation
  ☐ A 4 same as P
  ☐ B 1 same as P
  ☐ C 4 opposite to P
  ☐ D 1 opposite to P

[1]

                        

ii)
Figure 11 shows the same arrangement with gear R replaced by a rack.


fig-11-paper2h-june2018-edexcel-gcse-physics

Figure 11

The rack can move up or down when the gears turn.

The teeth on the rack are 2 mm apart.

Calculate how far the rack moves when P turns through to one complete revolution.

[2]

distance = ............................................... mm

How did you do?

2b4 marks
Figure 12 shows three toy animals hanging from a rod.

The rod hangs from the ceiling by a string tied to the centre of the rod.

The system is in equilibrium.

fig-12-paper2h-june2018-edexcel-gcse-physicsFigure 12


Use the principle of moments to calculate the mass of the toy elephant.

How did you do?

2c3 marks
Figure 13 shows a diagram of a device for lifting heavy loads.

fig-13-paper2h-june2018-edexcel-gcse-physics
Figure 13

The metal tube is filled with oil.

The piston Y is pushed down with a force K.

This produces a force L on piston Z.

The pressure exerted on the oil by piston Y is the same as the pressure exerted by the oil on piston Z.

Explain the difference between the size of force K and the size of force L.

How did you do?

Did this page help you?

3a
Sme Calculator1 mark

Higher Only

 

Figure 1 shows some forces acting on a seesaw.

The forces shown have the same magnitude but act in different directions.

fig-1-paper2h-june2020-edexcel-gcse-physics

Figure 1

In which of these could the forces acting on a seesaw be in equilibrium?

  ☐ A  
  ☐ B  
  ☐ C  
  ☐ D  

How did you do?

3b
Sme Calculator2 marks

Higher Only

 

Figure 2 shows an open door.

fig-2-paper2h-june2020-edexcel-gcse-physics

Figure 2

Explain why it is easier to close the door by pushing at point P rather than pushing at point Q.

How did you do?

3c
Sme Calculator3 marks

Higher Only

 

Figure 3 is a diagram of the forces acting on a swing.
The swing is not moving.

fig-3-paper2h-june2020-edexcel-gcse-physics

Figure 3

The seat of the swing, AB, is 0.80 m long. A person of weight 450 N sits on the seat. The person’s weight acts at a distance of 0.50 m from A as shown in Figure 3.

Ignore the weight of the seat.

The upward forces exerted by the ropes on the seat are F1 and F2.

Calculate the force F2 by taking moments about A.


force F2 = ...............................N

How did you do?

Did this page help you?