Total Internal Reflection (Edexcel GCSE Physics) : Revision Note
Did this video help you?
Total Internal Reflection
As the angle of incidence is increased, the angle of refraction also increases until it gets closer to 90°
When the angle of refraction is exactly 90° the light is refracted along the boundary
At this point, the angle of incidence is known as the critical angle θc
Total internal reflection (TIR) occurs when:
The angle of incidence is greater than the critical angle and the incident material is denser than the second material
Therefore, the two conditions for total internal reflection are:
The angle of incidence > the critical angle (i > θc)
The incident material is denser than the second material
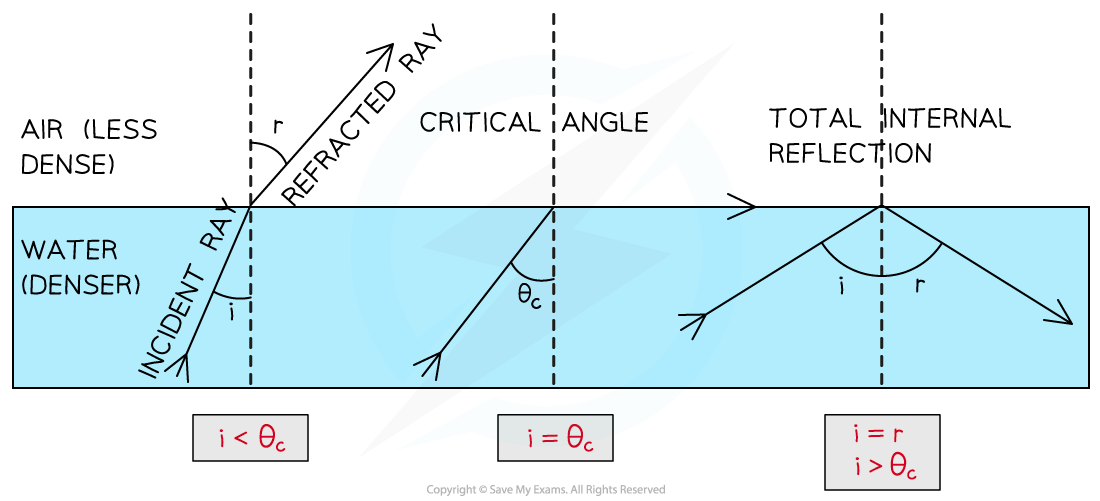
Critical angle and total internal reflection
Worked Example
A glass cube is held in contact with a liquid and a light ray is directed at a vertical face of the cube. The angle of incidence at the vertical face is 39° and the angle of refraction is 25° as shown in the diagram. The light ray is totally internally reflected for the first time at X.
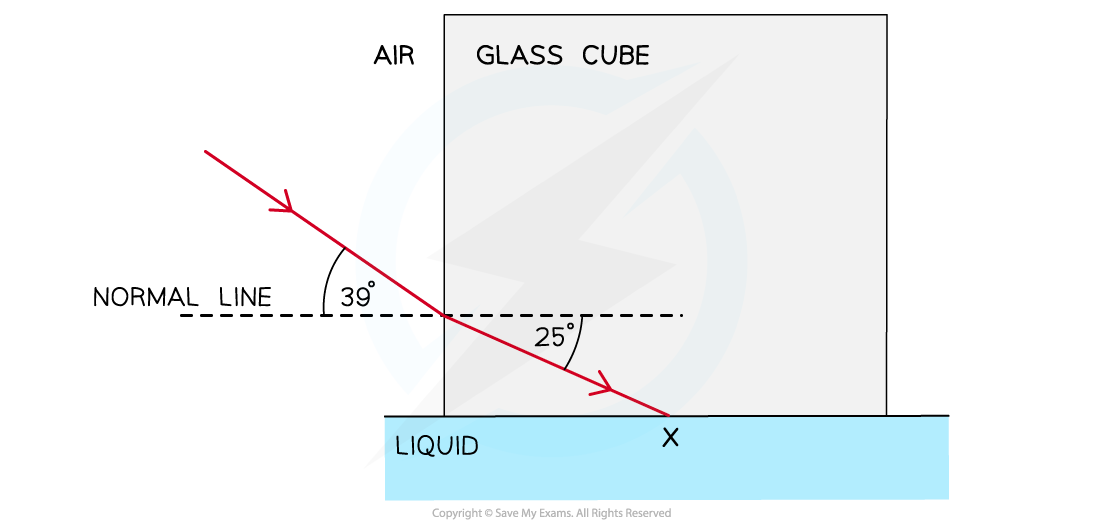
Complete the diagram to show the path of the ray beyond X to the air and calculate the critical angle for the glass-liquid boundary.
Answer:
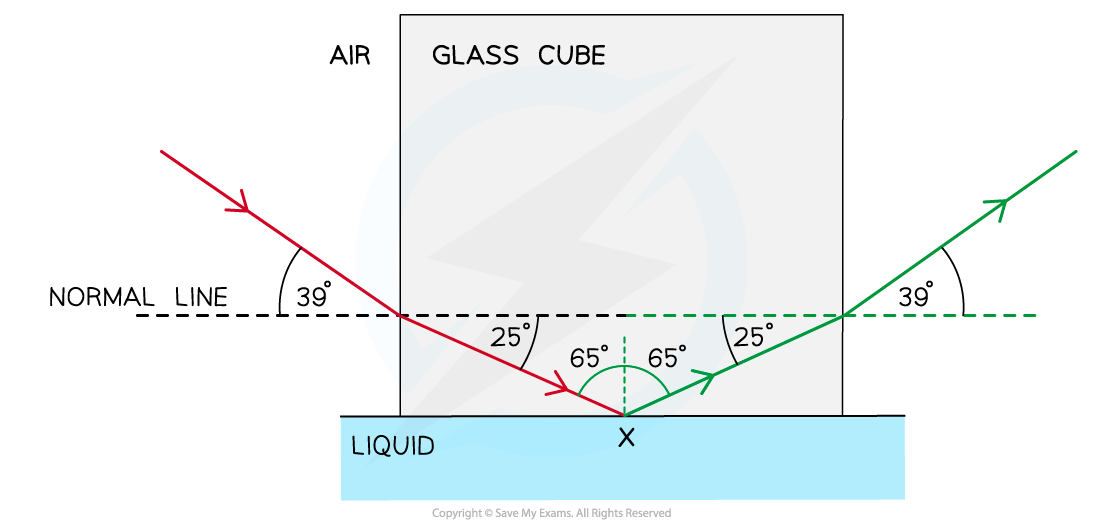
Step 1: Draw the reflected angle at the glass-liquid boundary
When a light ray is reflected, the angle of incidence = angle of reflection (i = r)
Therefore, the angle of incidence (or reflection) is 90° – 25° = 65°
Step 2: Draw the refracted angle at the glass-air boundary
At the glass-air boundary, the light ray refracts away from the normal
Due to the reflection, the light rays are symmetrical to the other side
Step 3: Calculate the critical angle
The question states the ray is “totally internally reflected for the first time” meaning that this is the lowest angle at which TIR occurs
Therefore, 65° is the critical angle

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
