Calculating Depth & Distance
Higher Tier Only
- If the speed of a wave is known, it can be used to calculate the distance to an object, or the depth of an object - say, underwater
Calculating Distance
- The worked example below demonstrates how the speed of sound in air can be used to determine how far away objects are from an observer
Worked example
A clap of thunder is heard 4 seconds after the corresponding flash of lightning.How far away is the thunderstorm? (The speed of sound in air is 330 m/s)
Step 1: List the known quantities
- Wave speed, v = 330 m/s
- Time, t = 4 s
Step 2: Write out the wave speed, distance and time formula
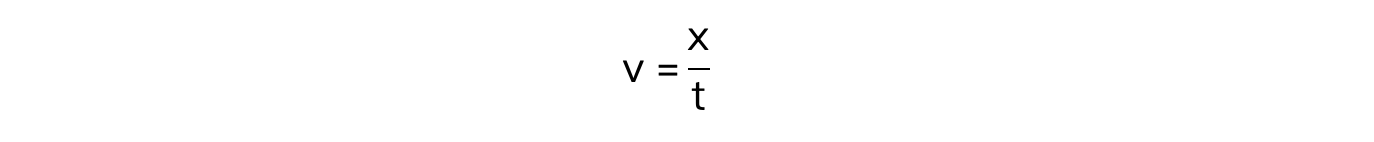
Step 3: Re-arrange the equation to make distance (x) the subject
x = v × t
Step 4: Put known values into the equation
x = 330 × 4 = 1320 m
- So the distance to the thunderstorm is 1320 m
Calculating Depth
- Echo sounding uses ultrasound to detect objects underwater
- The sound wave is reflected off the ocean bottom
- The time it takes for the sound wave to return is used to calculate the depth of the water
- The distance the wave travels is twice the depth of the ocean
- This is the distance to the ocean floor plus the distance for the wave to return
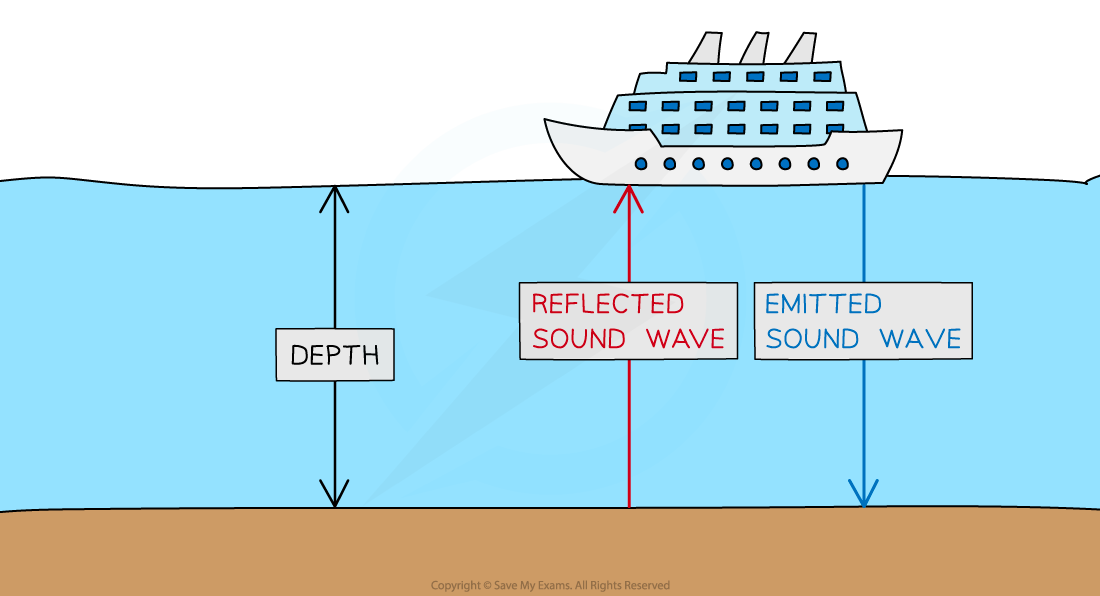
Echo sounding is used to determine water depth
Worked example
The sound wave released from a ship took 0.12 seconds to return. The speed of sound in water is 1500 m/s.What was the depth of the sea?
Step 1: List the known quantities
- Wave speed, v = 1500 m/s
- Time, t = 0.12 s
Step 2: Write out the wave speed, distance and time formula
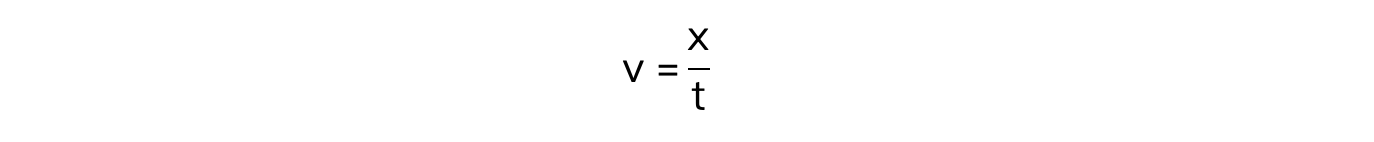
Step 3: Rearrange the equation to make distance (x) the subject
x = v × t
Step 4: Put known values into the equation
x = 1500 × 0.12 = 180 m
Step 5: Half the distance to obtain the depth
d = 180 ÷ 2
Depth, d = 90 m
Examiner Tip
Don't forget to take into account if a sound wave has travelled twice the distanceYou can do this one of two ways:
- Halve the time at the beginning, or
- Halve the distance at the end
