Conservation of Energy (Edexcel GCSE Physics)

Closed Systems

• In physics, a system is defined as:

  An object or group of objects

• Defining a system in physics is a way of narrowing the parameters to focus only on what is relevant to the situation being observed

• When a system is in equilibrium, nothing changes and so nothing happens

• When there is a change in a system, energy is transferred

• An apple sitting on a table can be defined as a system

• If nothing changes, the apple will just sit there

• If the table is removed, the apple will fall

• As the apple falls, energy is transferred

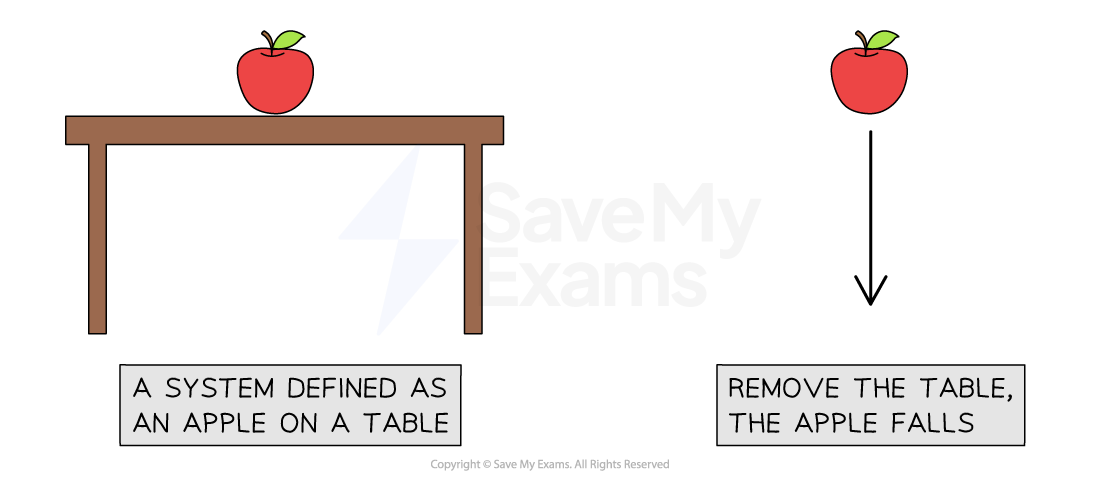
A change in a system causes a transfer of energy from the apple's gravitational potential store to its kinetic store

• Energy is measured in units of joules (J)

• A  closed system is defined as:

  A system where there is no net change to the total energy in that system

• As a result, the total amount of energy within that system must remain constant

  • This is due to the conservation of energy

Conservation of Energy

• The principle of conservation of energy states that:

  Energy cannot be created or destroyed, it can only be transferred from one store to another

• This means the total amount of energy in a closed system remains constant 

• The total energy transferred into a system must be equal to the total energy transferred out of the system

• Therefore, energy is never 'lost' but it can be transferred to the surroundings

  • Energy can be dissipated (spread out) to the surroundings by heating and radiation

  • Dissipated energy transfers are often not useful, and can then be described as wasted energy

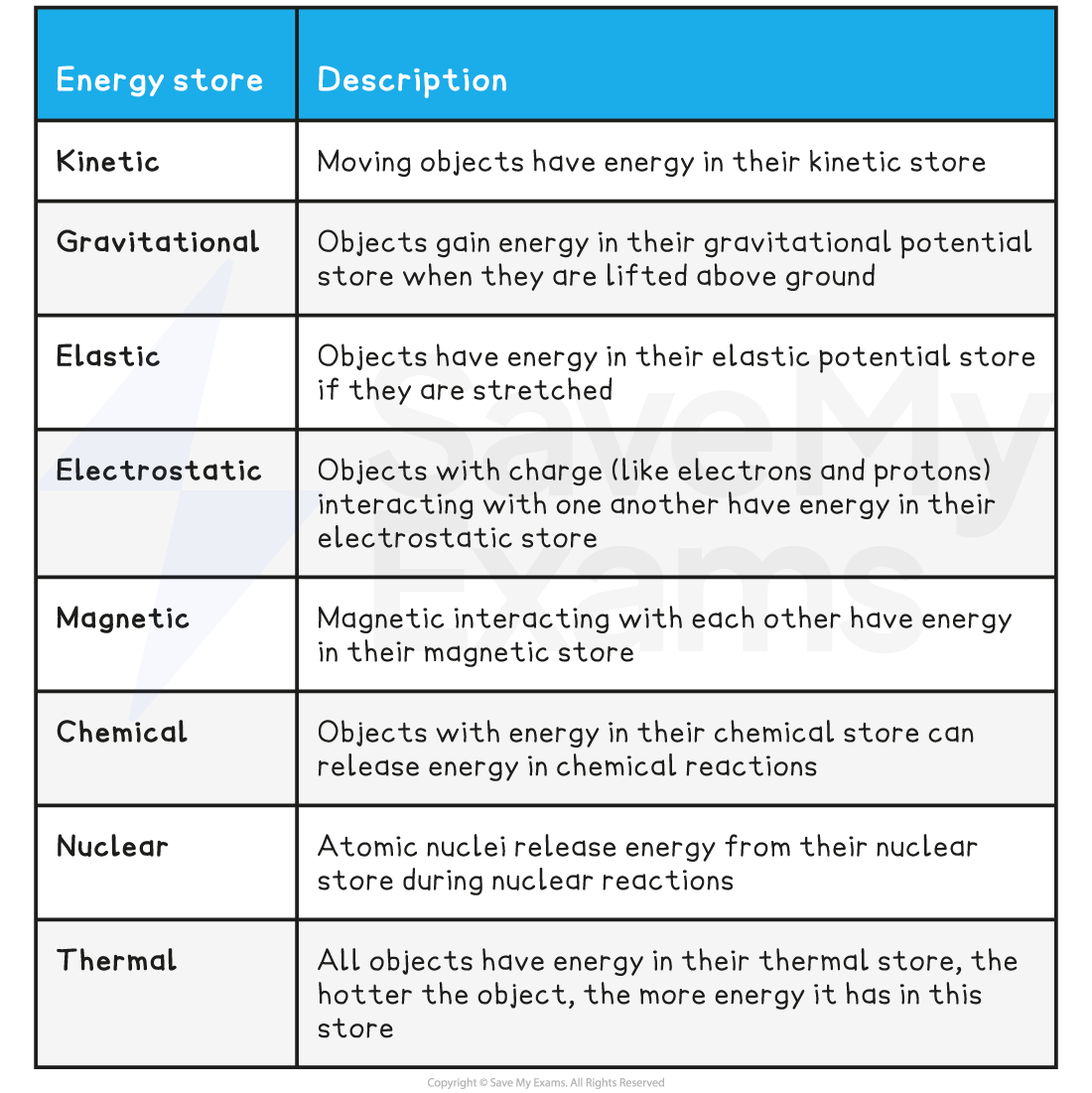
Energy Stores

• Energy is stored in objects in different energy stores

Energy Stores Table

Energy Transfer Pathways

• Energy is transferred between stores via transfer pathways

• Examples of these are:

  • Mechanically

  • Electrically

  • By heating

  • By radiation

• These are described in the table below:

Energy Transfer Pathway Table

• An example of an energy transfer is a hot coffee heating cold hands

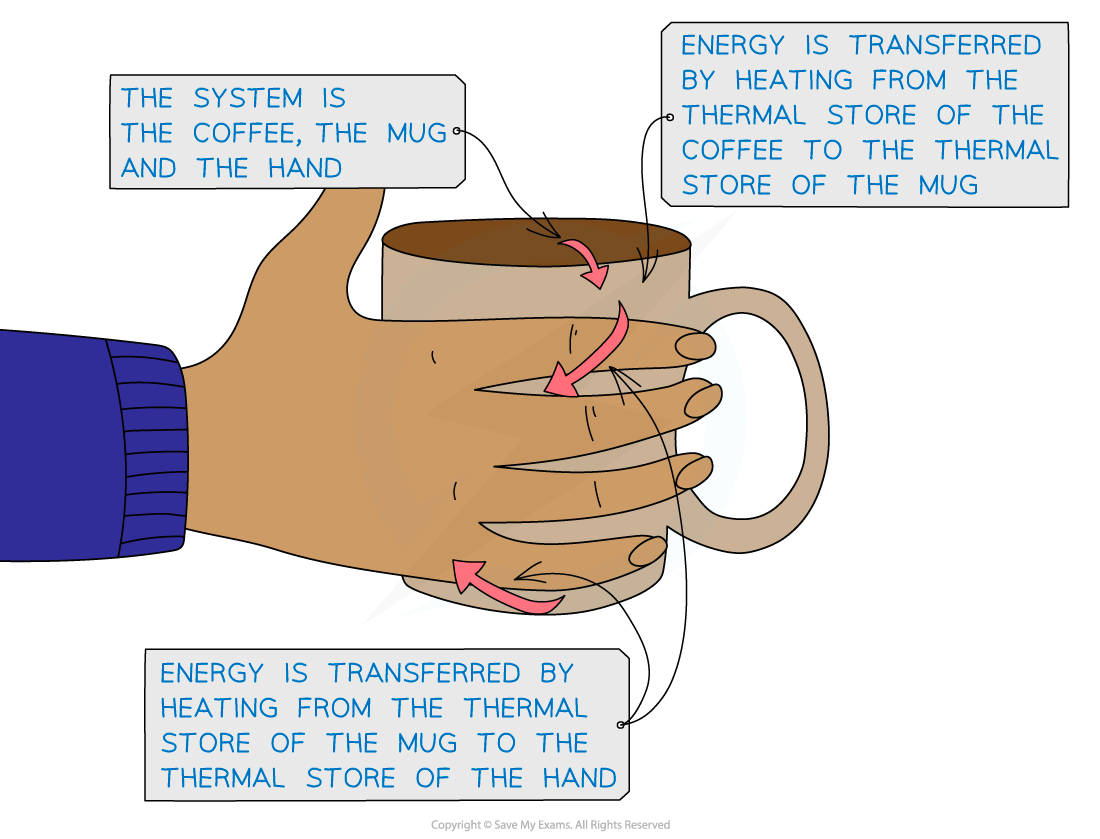
Energy is transferred by heating from the hot coffee to the mug to the cold hands

Representing Energy Transfers

Energy Flow Diagrams

• Energy stores and transfers can be represented using a flow diagram

  • This shows both the stores and the transfers taking place within a system

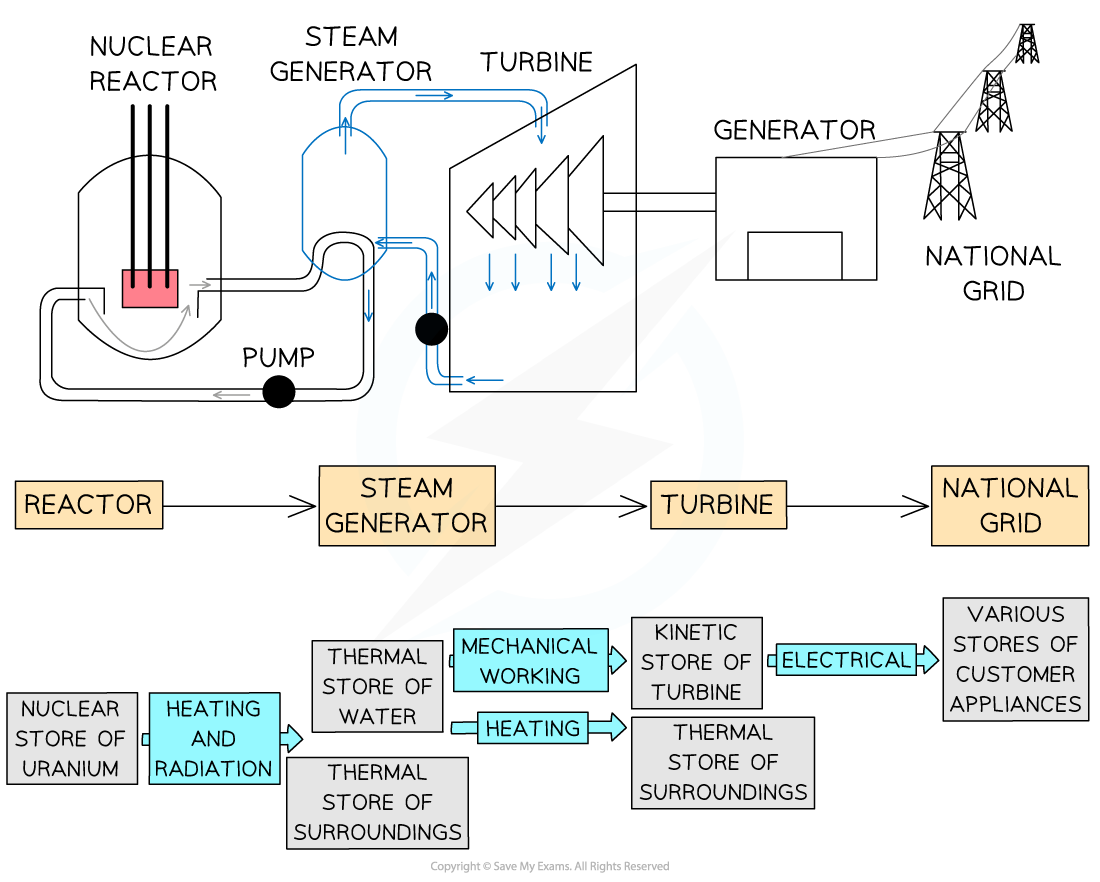
Energy flow diagram showing energy stores and transfers in a nuclear power plant.

Note the colour difference of the labels (stores) and the arrows (transfer pathways) 

Sankey Diagrams

• Sankey diagrams can be used to represent energy transfers

  • Sankey diagrams are characterised by the splitting arrows that show the proportions of the energy transfers taking place

• The different parts of the arrow in a Sankey diagram represent the different energy transfers:

  • The left-hand side of the arrow (the flat end) represents the energy transferred into the system

  • The straight arrow pointing to the right represents the energy that ends up in the desired store; this is the useful energy output

  • The arrows that bend away represent the wasted energy

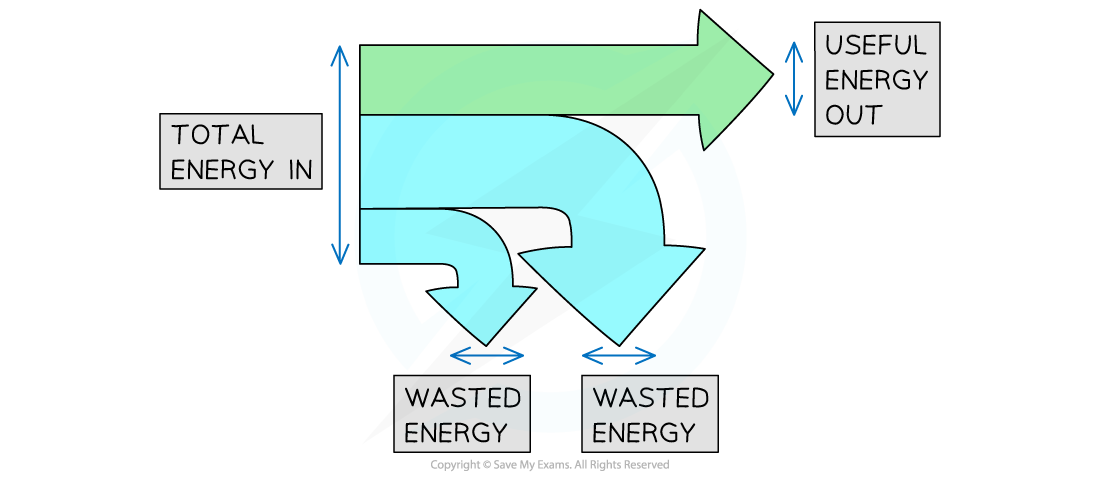
Total energy in, wasted energy and useful energy out shown on a Sankey diagram

• The width of each arrow is proportional to the amount of energy being transferred

• As a result of the conversation of energy:

Total energy in = Useful energy out + Wasted energy

• A Sankey diagram for a modern efficient light bulb will look very different from that for an old filament light bulb

• A more efficient light bulb has less wasted energy

  • This is shown by the smaller arrow downwards representing the heat energy

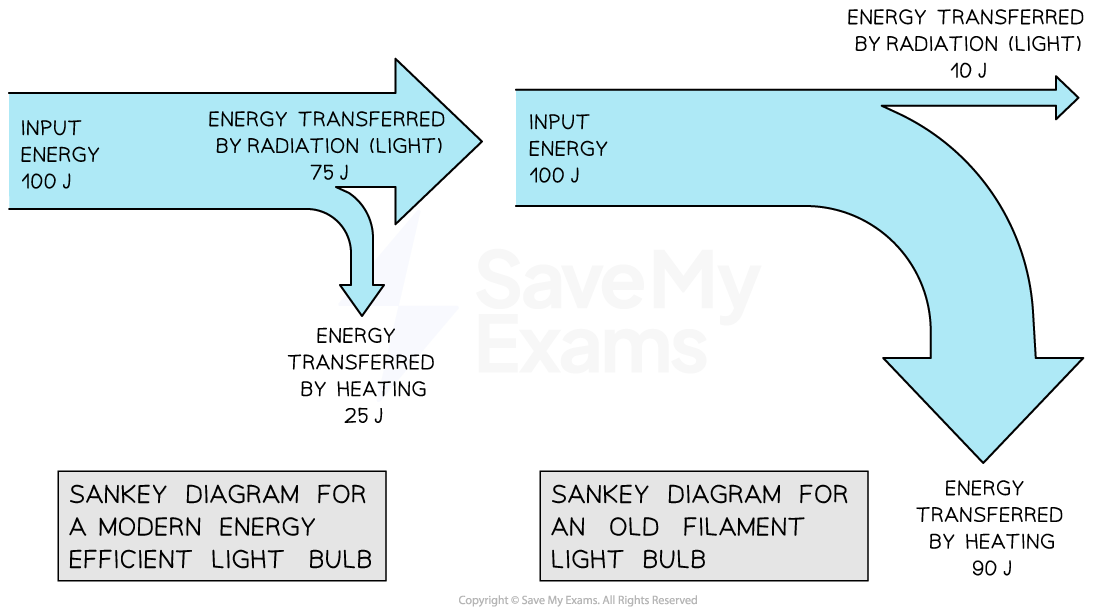
Sankey diagram for modern vs. old filament light bulb