Calculating Stopping Distances (Edexcel GCSE Physics) : Revision Note
Estimating Stopping Distances
For a given braking force, the speed of a vehicle determines the size of the stopping distance
The greater the speed of the vehicle, the larger the stopping distance
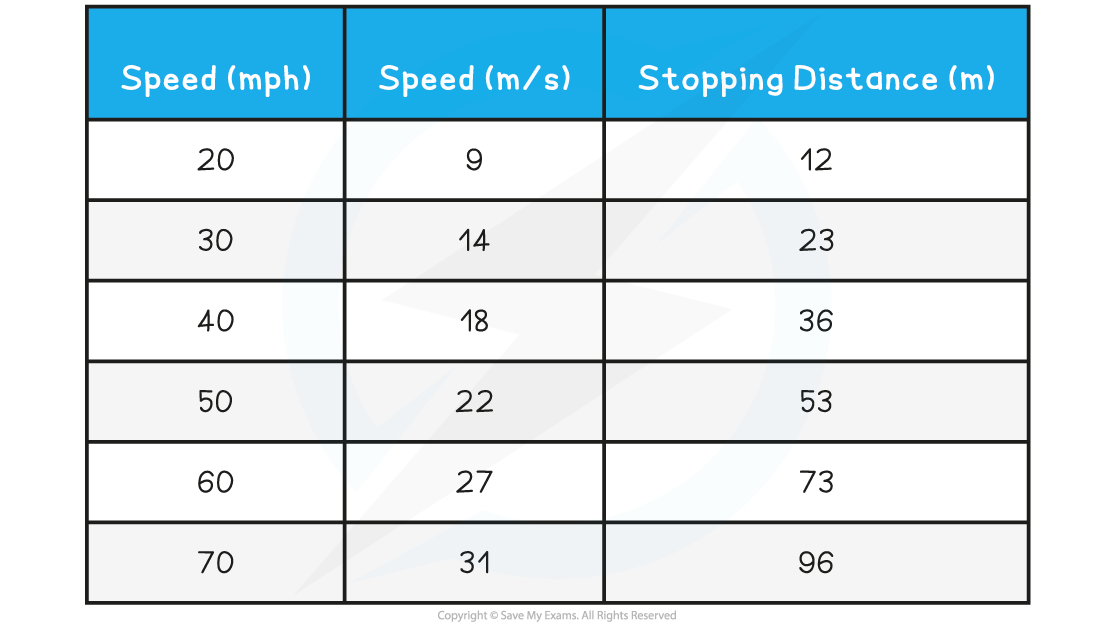
The image below shows how the stopping distance of a typical family car increases with increasing speed:
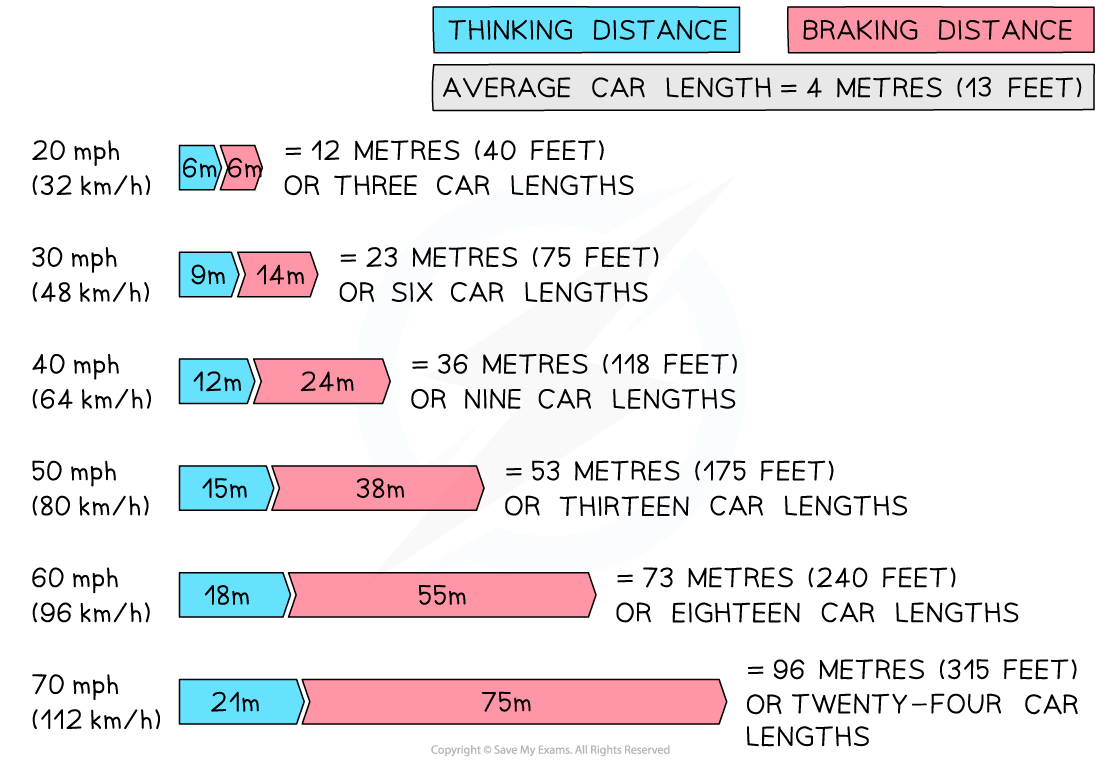
A vehicle's stopping distance increases with speed. At a speed of 20 mph the stopping distance is 12 m, whereas at 60 mph the stopping distance is 73 m (reproduced from the UK Highway Code under the
Worked Example
A car is travelling with a velocity of 100 miles per hour. Use the information provided in the diagram above to estimate the thinking, braking and stopping distance for the car.
Answer:
Step 1: Identify the variables
The diagram contains information for a car at a velocity of 50 mph as follows:
Thinking distance = 15 m
Braking distance = 38 m
Stopping distance = 53 m
The new speed is 100 mph which is double the velocity in the diagram
Step 2: State the relationship between thinking and braking distance, and velocity
Thinking distance is proportional to the velocity
Braking distance is proportional to the velocity squared
Step 3: Calculate the new thinking and braking distances
Thinking distance at 100 mph = 15 × 2 = 30 m
Braking distance at 100 mph = 38 × 4 = 152 m
Step 4: Calculate the new stopping distance
Stopping distance = Thinking distance + Braking distance
Stopping distance = 30 + 152 = 182 m
Calculating Braking Distance
When a vehicle stops work is done by a force
The kinetic energy of the car is transferred to thermal energy in the brakes which does work
This can also be represented by the braking force and braking distance by the following equation:

This equation shows that the work done is the transfer of kinetic energy
We can use this equation to estimate the decelerating forces required for a typical vehicle moving at everyday speeds
This equation can be rearranged to show how the braking distance depends on velocity:

Equation for braking distance from mass, velocity and braking force
The braking distance is proportional to the vehicle's velocity squared
For example, if the velocity of the vehicle doubles then the braking distance will increase by a factor of 4
Worked Example
At 18 m/s (40 mph) the braking distance of a typical car of mass 1500 kg is about 24 m. Use this information to estimate the braking force for a typical car.
Answer:

Examiner Tips and Tricks
The equation for braking distance doesn't actually apply at very high speeds because the brakes get hot and become less effective. This reduces the braking force, causing the braking distance to increase even further. This is why it is important to prevent brakes from overheating.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
