Stopping Distances (Edexcel GCSE Physics) : Revision Note
Did this video help you?
Thinking & Braking Distances
The stopping distance of a car is defined as:
The total distance travelled during the time it takes for a car to stop in response to some emergency
It can be written as an equation involving two distances:
Stopping distance = Thinking distance + Braking distance
Where:
Thinking distance = the distance travelled in the time it takes the driver to react (reaction time) in metres (m)
Braking distance = the distance travelled under the braking force in metres (m)
Stopping distance = the sum of the thinking distance and braking distance, in metres (m)
For a given braking force, the greater the speed of the vehicle, the greater the stopping distance
Worked Example
At a speed of 20m/s, a particular vehicle had a stopping distance of 40 metres. The car travelled 14 metres whilst the driver was reacting to the incident in front of him. What was the braking distance?
A. 54 m
B. 34 m
C. 26 m
D. 6 m
Answer: C
Step 1: Identify the different variables
The stopping distance is 40 metres
The car travelled 14 metres while the driver was reacting
This is the thinking distance
Step 2: Rearrange the formula for stopping distance
Stopping distance = Thinking distance + Braking distance
Braking distance = Stopping distance – Thinking distance
Step 3: Calculate the correct braking distance
Braking distance = 40 – 14 = 26 metres
Dangers on the Road
A large deceleration can be dangerous for a number of different reasons
For any object to decelerate, a force is required and for heavy objects, large decelerations will require large forces
This is true according to Newton’s Second Law:
F = ma
Where:
F = force in newtons (N)
m = mass in kilograms (kg)
a = acceleration in metres per second squares (m/s2)
This equation can be rearranged with the help of a formula triangle:
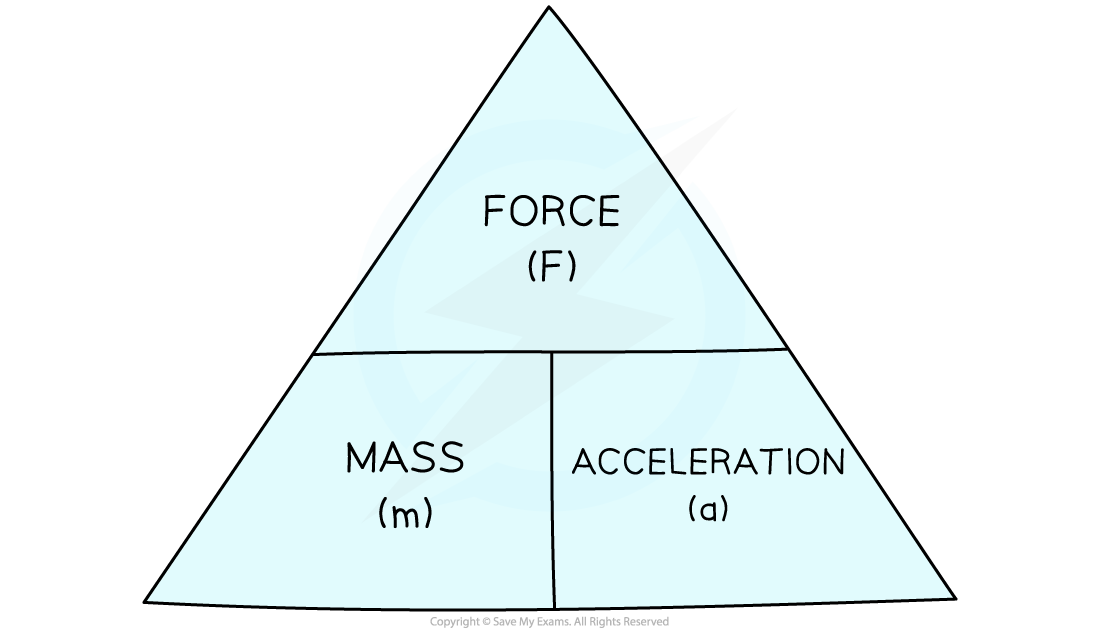
Force, mass, acceleration formula triangle
Overheating of Brakes
Vehicles use brakes to decelerate
These reduce the speed of the vehicle by creating a friction force between the brake and the wheel
The kinetic energy of the vehicle is converted to thermal energy of the brakes
If brakes get too hot then they can fail, meaning that they will not work effectively the next time they are used
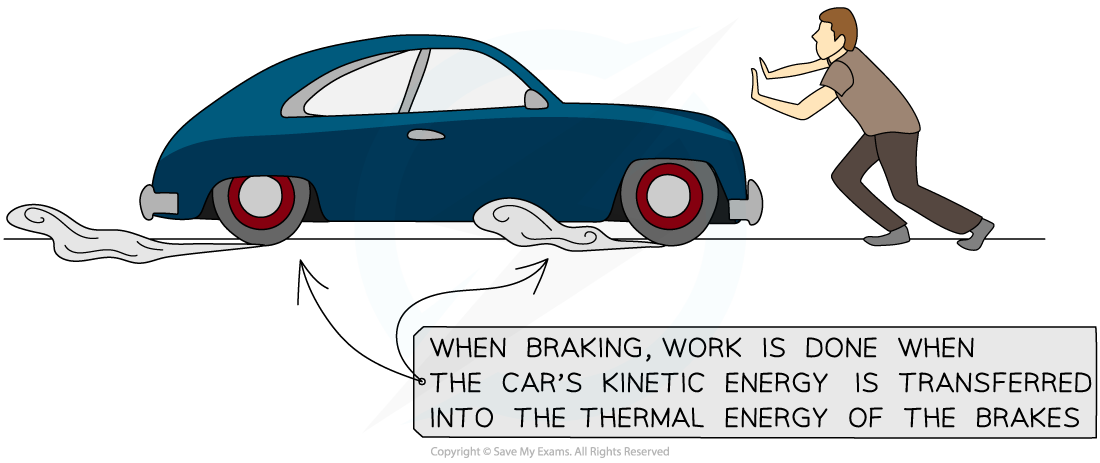
Work done by breaking transfers kinetic into thermal energy
Loss of Control and Injury
When a vehicle undergoes a deceleration then the driver and passengers also experience a deceleration
This can cause injuries such as whiplash is a neck injury caused when a persons head moves suddenly, relative to their body
It is also more difficult to control a vehicle that is decelerating
Losing control can cause a collision
Worked Example
A passenger travels in a car at a moderate speed. The vehicle is involved in a collision, which brings the car (and the passenger) to a halt in 0.1 seconds. Estimate:
a) The acceleration of the car (and the passenger).
b) The force on the passenger.
Answer:
Part (a)
Step 1: Estimate the required quantities and list the known quantities
A moderate speed for a car is about 50 mph or 20 m/s
Initial velocity ~ 20 m/s
Final velocity = 0 m/s
Time, t = 0.1 s
Step 2: Calculate the change in velocity of the car (and the passenger)
change in velocity = Δv = final velocity − initial velocity
Δv = 0 − 20
Δv = −20 m/s
Step 3: Calculate the acceleration of the car (and the passenger) using the equation:

Step 4: Calculate the deceleration
a = −20 ÷ 0.1
a ~ −200 m/s2
Part (b)
Step 1: Estimate the required quantities and list the known quantities
An adult person has a mass of about 70 kg
Mass of the passenger, m ~ 70 kg
Acceleration, a = −200 m/s2
Step 2: State Newton's second law
This question involves quantities of force, mass and acceleration, so the equation for Newton's second law is:
F = ma
Step 3: Calculate an estimate for the decelerating force
F = 70 × −200
F ~ −14 000 N
Examiner Tips and Tricks
Remember that resultant force is a vector quantity. Examiners may ask you to comment on why its value is negative - this happens when the resultant force acts in the opposite direction to the object's motion. In the worked example above, the resultant force opposes the passenger's motion, slowing them down (decelerating them) to a halt, this is why it has a minus symbol.

You've read 1 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
