Stopping Distances (Edexcel GCSE Physics)

• The stopping distance of a car is defined as:

The total distance travelled during the time it takes for a car to stop in response to some emergency

• It can be written as an equation involving two distances:

Stopping distance = Thinking distance + Braking distance

• Where:
  • Thinking distance = the distance travelled in the time it takes the driver to react (reaction time) in metres (m)
  • Braking distance = the distance travelled under the braking force in metres (m)
  • Stopping distance = the sum of the thinking distance and braking distance, in metres (m)

• For a given braking force, the greater the speed of the vehicle, the greater the stopping distance

ANSWER: C

Step 1: Identify the different variables

• • The stopping distance is 40 metres
  • The car travelled 14 metres while the driver was reacting
    • This is the thinking distance

Step 2: Rearrange the formula for stopping distance

Stopping distance = Thinking distance + Braking distance

Braking distance = Stopping distance – Thinking distance

Step 3: Calculate the correct braking distance

• • Braking distance = 40 – 14 = 26 metres

• A large deceleration can be dangerous for a number of different reasons
• For any object to decelerate, a force is required and for heavy objects, large decelerations will require large forces
• This is true according to Newton’s Second Law:

F = ma

• Where:
  • F = force in newtons (N)
  • m = mass in kilograms (kg)
  • a = acceleration in metres per second squares (m/s²)

• This equation can be rearranged with the help of a formula triangle:

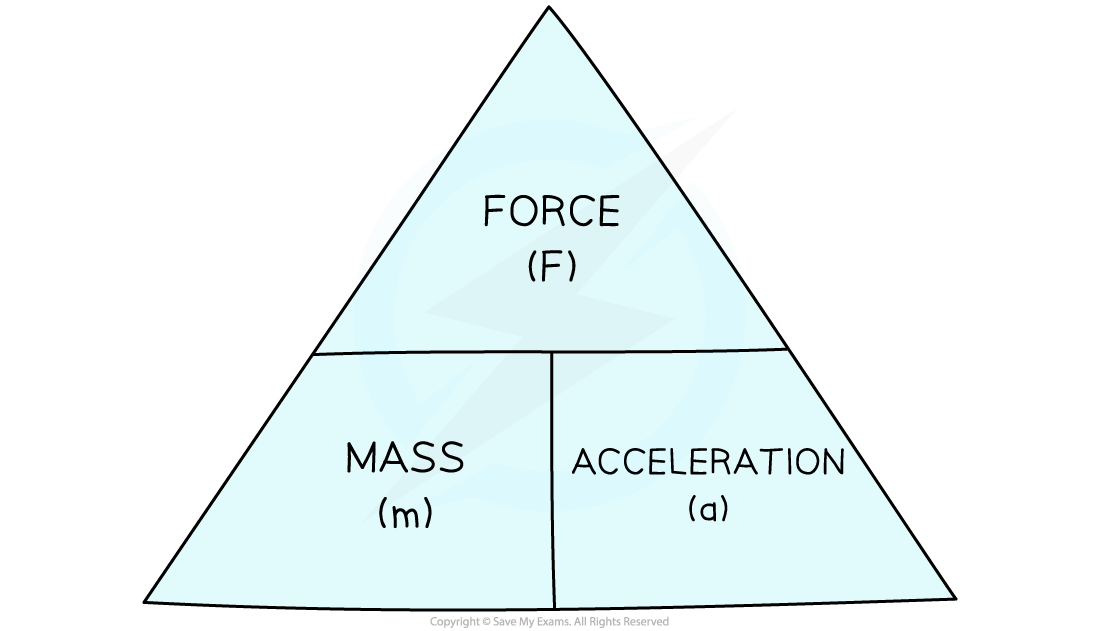
Force, mass, acceleration formula triangle

Overheating of Brakes

• Vehicles use brakes to decelerate
• These reduce the speed of the vehicle by creating a friction force between the brake and the wheel
• The kinetic energy of the vehicle is converted to thermal energy of the brakes
• If brakes get too hot then they can fail, meaning that they will not work effectively the next time they are used

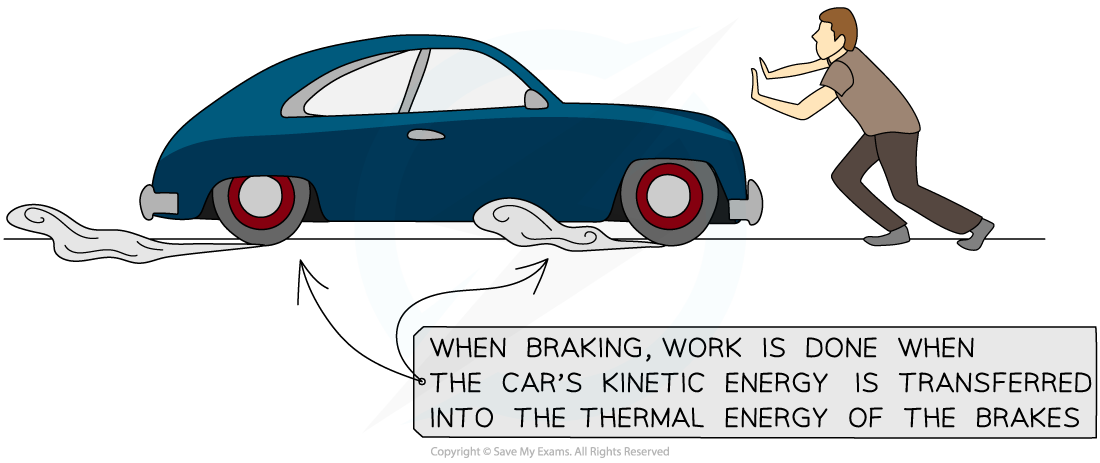
Work done by breaking transfers kinetic into thermal energy

Loss of Control and Injury

• When a vehicle undergoes a deceleration then the driver and passengers also experience a deceleration
• This can cause injuries such as whiplash is a neck injury caused when a persons head moves suddenly, relative to their body
• It is also more difficult to control a vehicle that is decelerating
• Losing control can cause a collision

Part (a)

Step 1: Estimate the required quantities and list the known quantities

A moderate speed for a car is about 50 mph or 20 m/s

• • Initial velocity ~ 20 m/s
  • Final velocity = 0 m/s
  • Time, t = 0.1 s

Step 2: Calculate the change in velocity of the car (and the passenger)

change in velocity = Δv = final velocity − initial velocity

Δv = 0 − 20

Δv = −20 m/s

Step 3: Calculate the acceleration of the car (and the passenger) using the equation:

Step 4: Calculate the deceleration

a = −20 ÷ 0.1

a ~ −200 m/s²

Part (b)

Step 1: Estimate the required quantities and list the known quantities

An adult person has a mass of about 70 kg

• • Mass of the passenger, m ~ 70 kg
  • Acceleration, a = −200 m/s²

Step 2: State Newton's second law 

• • This question involves quantities of force, mass and acceleration, so the equation for Newton's second law is:

F = ma

Step 3: Calculate an estimate for the decelerating force

F = 70 × −200

F ~ −14 000 N