Conservation of Momentum (Edexcel GCSE Physics): Revision Note
Exam code: 1PH0
Conservation of Momentum
Higher Tier Only
The principle of conservation of momentum states that:
In a closed system, the total momentum before an event is equal to the total momentum after the event
A closed system means the energy within the system is constant and there is an absence of external forces (e.g. friction)
In other words:
The total momentum before a collision = The total momentum after a collision
A system is a certain number of objects under consideration
This can be just one object or multiple objects
Since momentum is a vector quantity, a system of objects moving in opposite directions (e.g. towards each other) at the same speed will have an overall momentum of 0 since they will cancel out
Momentum is always conserved over time
The diagram below shows two masses m with velocity u and M at rest (ie. zero velocity)
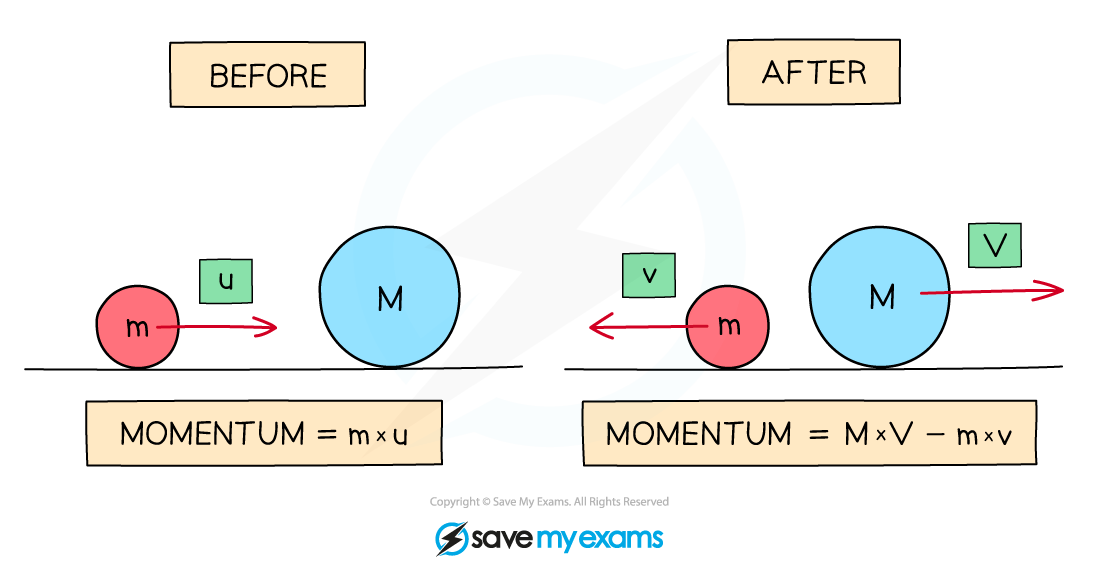
The momentum of a system before and after a collision
Before the collision:
The momentum is only of mass m which is moving
If the right is taken as the positive direction, the total momentum of the system is m × u
After the collision:
Mass M also now has momentum
The velocity of m is now -v (since it is now travelling to the left) and the velocity of M is V
The total momentum is now the momentum of M + momentum of m
This is (M × V) + (m × -v) or (M × V) – (m × v)
Worked Example
The diagram shows a car and a van, just before and just after the car collided with the van, which is initially at rest.
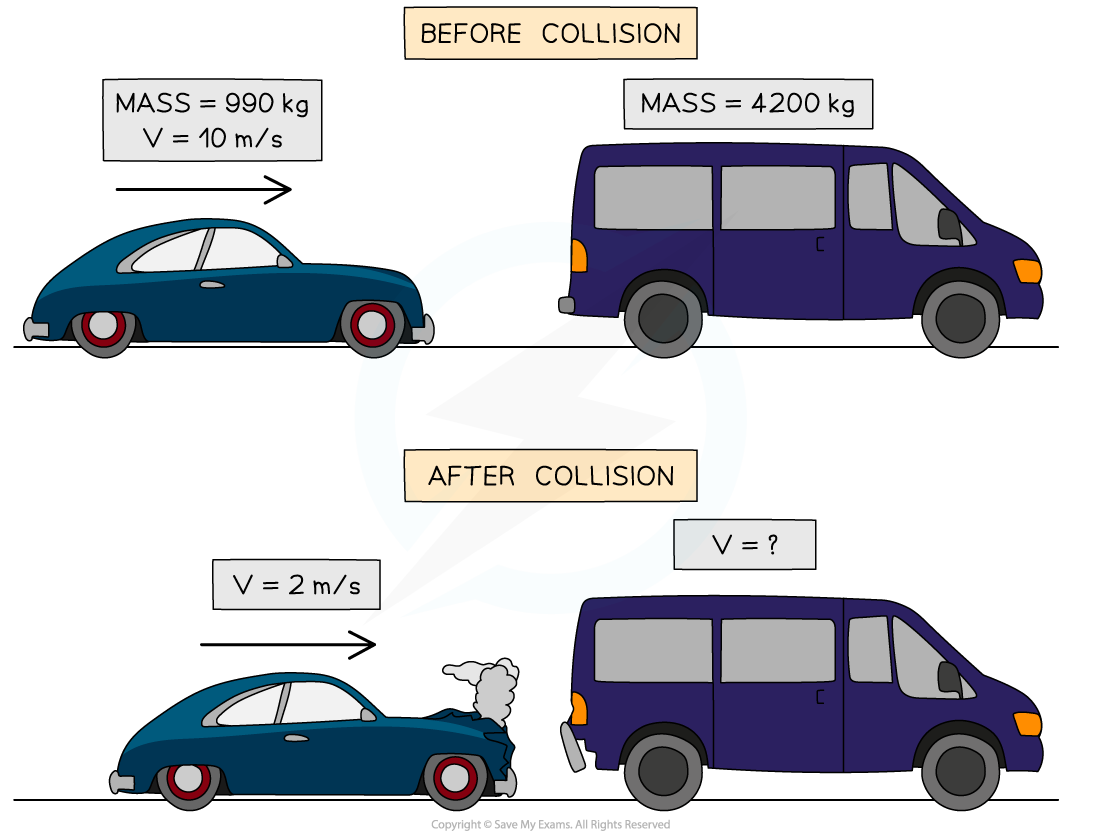
Use the idea of conservation of momentum to calculate the velocity of the van when it is pushed forward by the collision.
Answer:


Examiner Tips and Tricks
If it is not given in the question already, drawing a diagram of before and after helps keep track of all the masses and velocities (and directions) in the conversation of momentum questions.
Newton's Third Law & Momentum
Higher Tier Only
Newton’s third law of motion states:
Whenever two bodies interact, the forces they exert on each other are equal and opposite
This means:
When one object exerts a force on another object, the second object will exert an equal force on the first object in the opposite direction
When two objects collide, both objects will react, generally causing one object to speed up (gain momentum) and the other object to slow down (lose momentum)
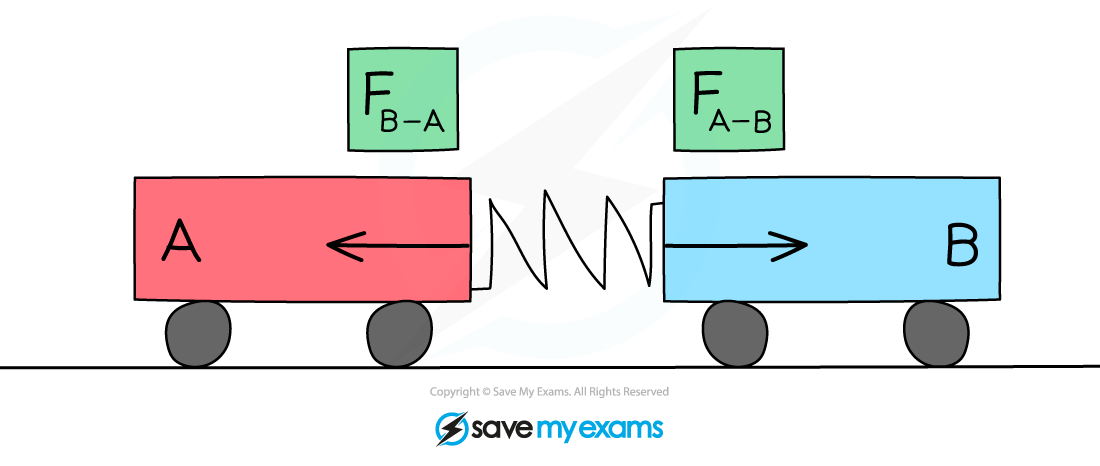
Newton's third law can be applied to collisions
Consider the collision between two trolleys, A and B:
When trolley A exerts a force on trolley B, trolley B will exert an equal force on trolley A in the opposite direction
In this case:
FB–A = –FA–B
While the forces are equal in magnitude and opposite in direction, the accelerations of the objects are not necessarily equal in magnitude
From Newton's second law, acceleration depends upon both force and mass, this means:
For objects of equal mass, they will have equal accelerations
For objects of unequal mass, they will have unequal accelerations
Examiner Tips and Tricks
Remember in Newton's Third law that the two forces should always be from different objects.

Unlock more, it's free!
Did this page help you?