Elastic Potential Energy (Edexcel GCSE Physics): Revision Note
Exam code: 1PH0
Elastic Potential Energy
When a spring is stretched or compressed by a force, work is done by the spring
Work done is the transfer of energy
The energy is transferred to its elastic potential energy store
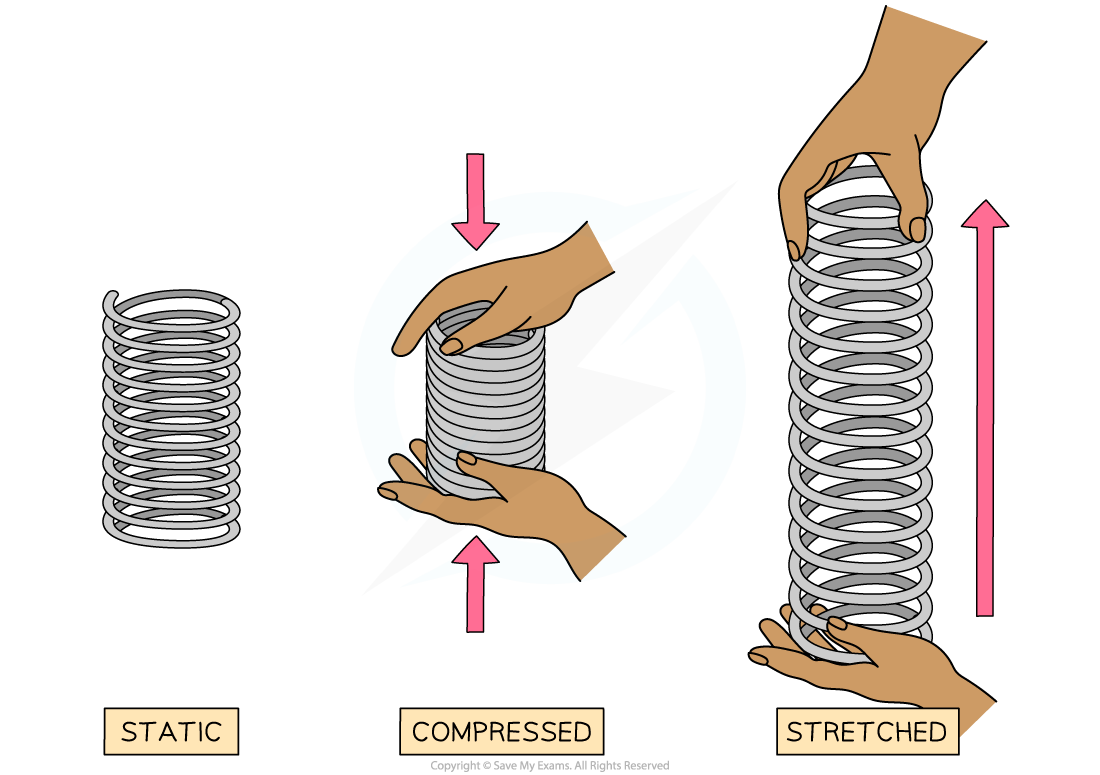
When a spring is stretched or compressed, there is work done and elastic potential energy is stored
Elastic potential energy is defined as:
The energy stored in an elastic object when work is done on the object
Provided the spring is not inelastically distorted (i.e has not exceeded its limit of proportionality), the work done on the spring and its elastic potential energy stored are equal
The work done, or the elastic potential energy stored, while stretching or compressing a spring can be calculated using the equation:
E = ½ kx2
Where:
E = elastic potential energy (energy transferred in stretching) in joules (J)
k = spring constant in newtons per metre (N/m)
x = extension in metres (m)

The elastic potential energy in a stretched spring depends on its spring constant and extension
This equation is only for springs that have not been stretched beyond their limit of proportionality
The term x2 means that if the extension is doubled then the work done is quadrupled
This is because 22 = 4
Worked Example
A mass is attached to the bottom of a hanging spring with a spring constant k and 0.2 J of work is done to stretch it by 4.5 cm. Calculate the spring constant, k for this spring.
Answer:

Examiner Tips and Tricks
Remember: when calculating the work done the extension, x, is squared (x2)!

Unlock more, it's free!
Did this page help you?