Conversions & Standard Form (Edexcel GCSE Physics)

Conversions

• As well as prefix (powers of ten) conversions (eg. km into m) there are also common unit conversions

• One such unit conversion are those for time

  • The main time conversions are shown in the table below:

Time Conversions Table

Hours & Seconds

• A common time unit conversion is between hours and seconds

  • 1 hour = 60 minutes

  • 1 minute = 60 seconds

• Therefore 1 hour = 60 × 60 = 3600 seconds

  • To convert from hours → seconds, multiply by 3600

  • To convert from seconds → hours, divide by 3600

Hours × 3600 = Seconds

Seconds ÷ 3600 = Hours  

Kelvin & Degrees Celsius

• A common temperature unit conversion is between Kelvin and degrees Celsius (ºC)

• The scale is defined as: 0 K = -273.15 ºC

  • To convert from Kelvin → Celsius, subtract 273.15

  • To convert from Celsius → Kelvin, add 273.15

 K − 273.15 = ^oC

  ^oC + 273.15 = K

Significant Figures & Standard Form

Significant Figures

• The significant digits are the digits in a number that contributes to the value of that number

  • These are sometimes called significant figures (s.f)

• In physics, values are rounded to a certain number of significant figures instead of decimal places

• Non-zero digits are always significant

  • 123 is 3 s.f

  • 1.78 is 3 s.f

• Any zeros between two significant digits are significant

  • 108 is 3 s.f

  • 10003 is 5 s.f

  • 1.006 is 4 s.f

• Only a final zero or trailing zeros in the decimal portion (after the decimal point) are significant

  • 0.183 is 3 s.f (the zero is before the decimal - so is not significant)

    • 1,8 and 3 are the significant figures

  • 1390 is 3 s.f. (the final zero is not after a decimal point - so is not significant)

    • 1,3 and 9 are the significant figures

  • 1.40 is 3 s.f (the final zero is after the decimal point - so is significant)

    • 1,4 and 0 are all the significant figures

  • 0.012 is 2 s.f (the zeros are either before the decimal point or is not the final zero - so not significant)

    • 1 and 2 are the significant figures

  • 1.9000 is 5 s.f (the trailing zeros are after the decimal point - so is significant)

    • 1, 9, 0, 0 and 0 are all the significant figures

• When rounding to a certain number of significant figures, this is done in a similar way to round to decimal places using the following procedure:

1. Find the number of significant figures to round to

2. Go to the digit for this significant figure

3. Look at the value after this digit

• If the value is 5 or greater, round this significant digit up

• If the value is less than 5, leave this significant digit as it is

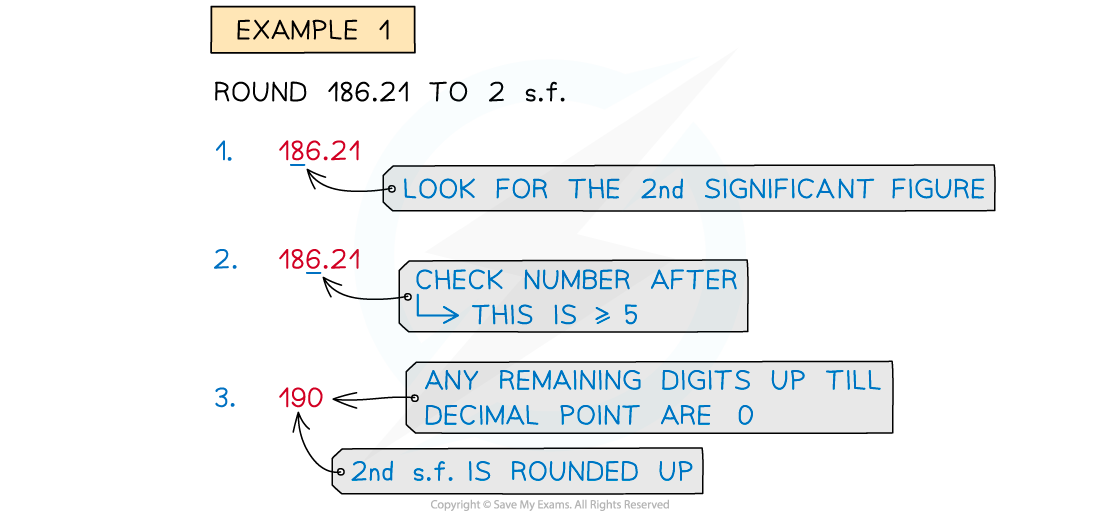
Rounding to 2 or 3 significant figures

Examples:

• The value 7.8 is 2 s.f

  • To 1 s.f this is equal to 8

• The value 9.12 is 3 s.f

  • To 2 s.f this is equal to 9.1

• The value 3.65 × 10^-4 is equal to 3.s.f

  • To 2 s.f this is equal to 3.7 × 10^-4

• The value 1020 is equal to 3 s.f

  • To 2 s.f this is equal to 1000

Standard Form

• Standard form is a system of writing large and small numbers which is useful for working with very large or very small numbers

  • This also means writing whole lines of zeros can be avoided

• Numbers in standard form are in written as:

a × 10ⁿ

• They follow these rules:

  • a is a number between 1 and 10

  • n > 0 for large numbers i.e how many times a is multiplied by 10

  • n < 0 for small numbers i.e how many times a is divided by 10

• For example:

  • 3 × 10⁸ = 300 000 000 (3 multiplied by 10, 8 times)

  • 2 × 10^-5 = 0.00002 (2 divided by 10, 5 times)

• When rounding a number in standard form to a certain number of significant figures, only the value of a is rounded (the × 10ⁿ value will not be significant)

  • For example, 5.18 × 10⁶ to 2 s.f. is 5.2 × 10⁶