Describe how the pressure beneath the surface of a liquid changes with depth and with density.
Complete the word equation defining pressure in liquids.
Pressure in a liquid is the _________ of the liquid × gravitational field strength × change in _________.
Higher Tier Only
Figure 1 shows a pair of identical objects in a column of liquid. One column is fresh water, and one column is salt water.
Figure 1
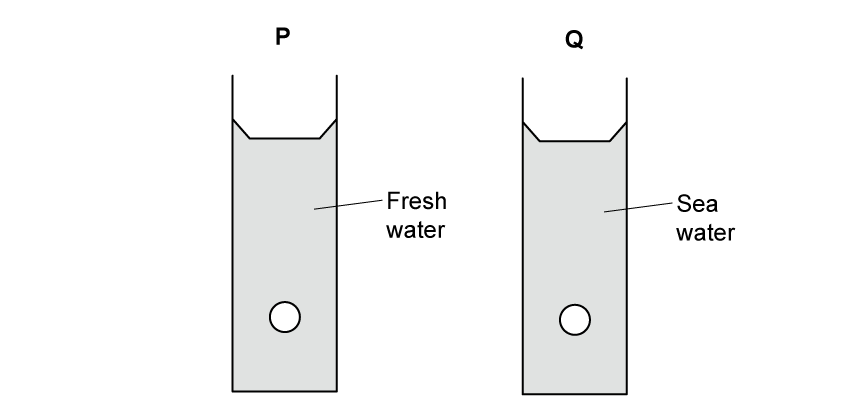
Explain which object, P or Q, experiences the highest pressure.
Higher Tier Only
Figure 2 shows the same pair of identical objects but the containers have been changed and both now contain fresh water.
Figure 2
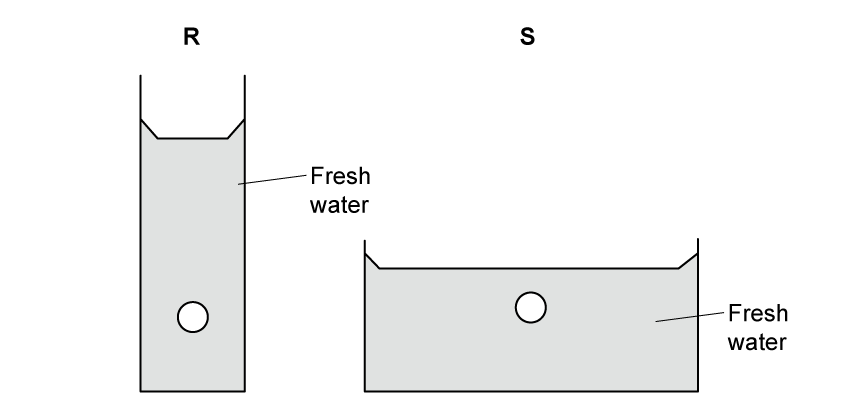
Explain which object, R or S, experiences the lowest pressure.
Did this page help you?












