Newton's Second Law (AQA GCSE Physics) : Revision Note
Did this video help you?
Newton's Second Law
Newton's second law of motion states:
The acceleration of an object is proportional to the resultant force acting on it and inversely proportional to the object's mass
Newton's second law explains the following important principles:
An object will accelerate (change its velocity) in response to a resultant force
The bigger this resultant force, the larger the acceleration
For a given force, the greater the object's mass, the smaller the acceleration experienced
The image below shows some examples of Newton's second law in action:
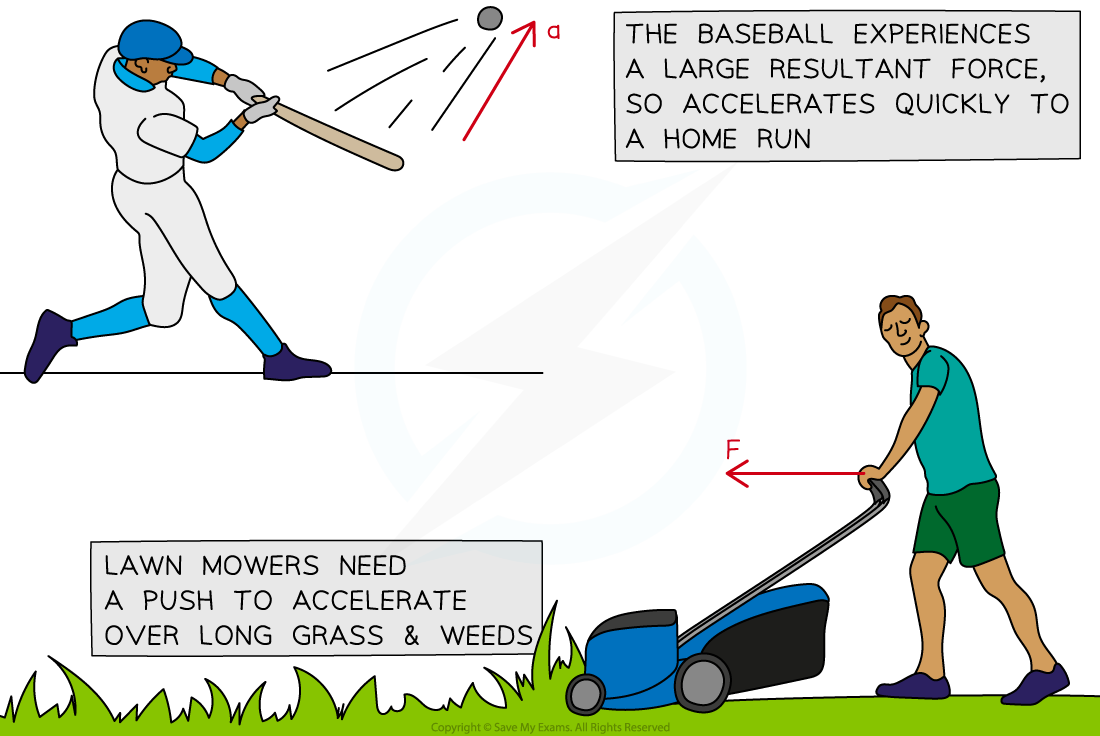
Objects like baseballs and lawnmowers accelerate when a resultant force is applied on them. The size of the acceleration is proportional to the size of the resultant force
Calculating Force & Acceleration
Newton's second law can be expressed as an equation:
F = ma
Where:
F = resultant force on the object in Newtons (N)
m = mass of the object in kilograms (kg)
a = acceleration of the object in metres per second squared (m/s2)
This equation can be rearranged with the help of a formula triangle:
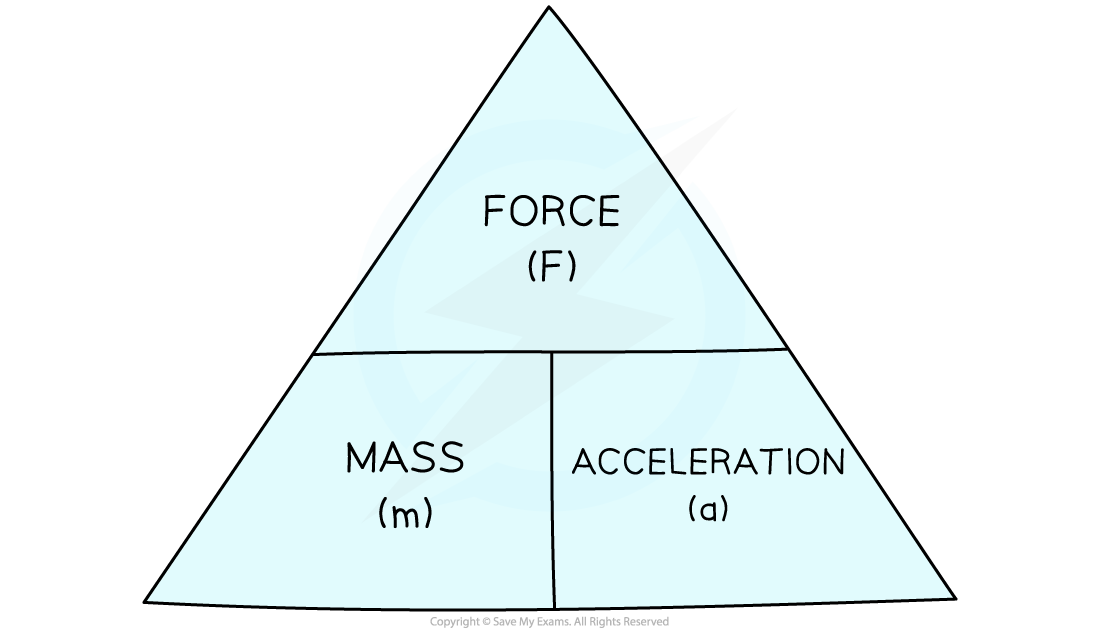
Force, mass, acceleration formula triangle
Worked Example
A car salesman says that his best car has a mass of 900 kg and can accelerate from 0 to 27 m/s in 3 seconds.
Calculate:
a) The acceleration of the car in the first 3 seconds.
b) The force required to produce this acceleration.
Answer:
Part (a)
Step 1: List the known quantities
Initial velocity = 0 m/s
Final velocity = 27 m/s
Time, t = 3 s
Step 2: Calculate the change in velocity
change in velocity = Δv = final velocity − initial velocity
Δv = 27 − 0 = 27 m/s
Step 3: State the equation for acceleration

Step 4: Calculate the acceleration
a = 27 ÷ 3 = 9 m/s2
Part (b)
Step 1: List the known quantities
Mass of the car, m = 900 kg
Acceleration, a = 9 m/s2
Step 2: Identify which law of motion to apply
The question involves quantities of force, mass and acceleration, so Newton's second law is required:
F = ma
Step 3: Calculate the force required to accelerate the car
F = 900 × 9 = 8100 N
Worked Example
Three shopping trolleys, A, B and C, are being pushed using the same force. This force causes each trolley to accelerate.

Which trolley will have the smallest acceleration? Explain your answer.
Answer:
Step 1: Identify which law of motion to apply
The question involves quantities of force and acceleration, and the image shows trolleys of different masses, so Newton's second law is required:
F = ma
Step 2: Re-arrange the equation to make acceleration the subject

Step 3: Explain the inverse proportionality between acceleration and mass
Acceleration is inversely proportional to mass
This means for the same amount of force, a large mass will experience a small acceleration
Therefore, trolley C will have the smallest acceleration because it has the largest mass
Estimating Speed, Acceleration & Force
Newton's second law can be used to estimate the sizes of forces and accelerations in realistic scenarios
When estimating quantities, an approximate answer can be shown using the symbol ~
For example, an adult person has a mass of ~70 kg
Worked Example
A passenger travels in a car at a moderate speed. The vehicle is involved in a collision, which brings the car (and the passenger) to a halt in 0.1 seconds.
Estimate:
a) The acceleration of the car (and the passenger).
b) The force on the passenger.
Answer:
Part (a)
Step 1: Estimate the required quantities and list the known quantities
A moderate speed for a car is about 50 mph or 20 m/s
Initial velocity ~ 20 m/s
Final velocity = 0 m/s
Time, t = 0.1 s
Step 2: Calculate the change in velocity of the car (and the passenger)
change in velocity = Δv = final velocity − initial velocity
Δv = 0 − 20
Δv = −20 m/s
Step 3: Calculate the acceleration of the car (and the passenger) using the equation:

Step 4: Calculate the deceleration
a = −20 ÷ 0.1
a ~ −200 m/s2
Part (b)
Step 1: Estimate the required quantities and list the known quantities
An adult person has a mass of about 70 kg
Mass of the passenger, m ~ 70 kg
Acceleration, a = −200 m/s2
Step 2: State Newton's second law
This question involves quantities of force, mass and acceleration, so the equation for Newton's second law is:
F = ma
Step 3: Calculate an estimate for the decelerating force
F = 70 × −200
F ~ −14 000 N
Examiner Tips and Tricks
Remember that resultant force is a vector quantity.
Examiners may ask you to comment on why its value is negative - this happens when the resultant force acts in the opposite direction to the object's motion.
In the worked example above, the resultant force opposes the passenger's motion, slowing them down (decelerating them) to a halt, this is why it has a minus symbol.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
