Resistors in Series & Parallel (AQA GCSE Physics) : Revision Note
Did this video help you?
Resistors in Series
When two or more resistors are connected in series, the total resistance is equal to the sum of their individual resistances
For two resistors of resistance R1 and R2, the total resistance can be calculated using:

Where R is the total resistance, in Ohms (Ω)
Increasing the number of resistors increases the overall resistance, as the charge now has more resistors to pass through
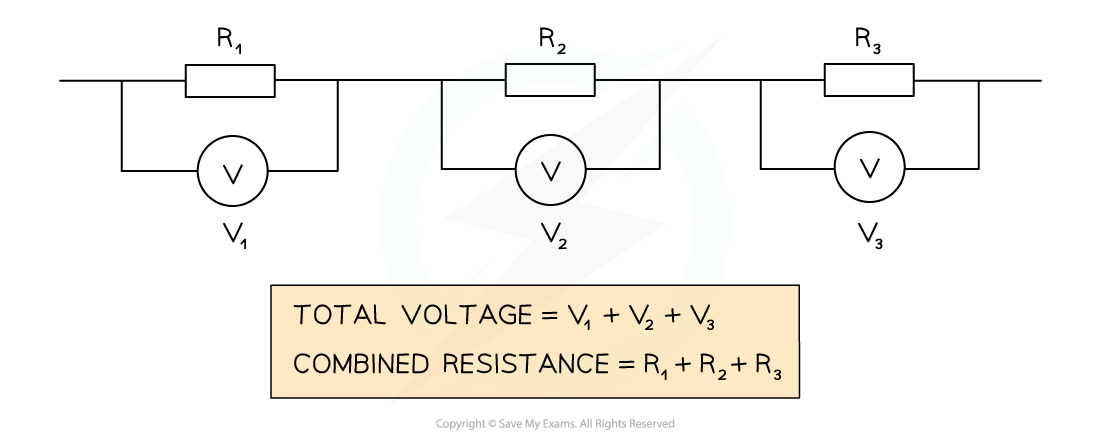
Resistors connected in series
Worked Example
The combined resistance R in the following series circuit is 60 Ω.What is the resistance value of R2?
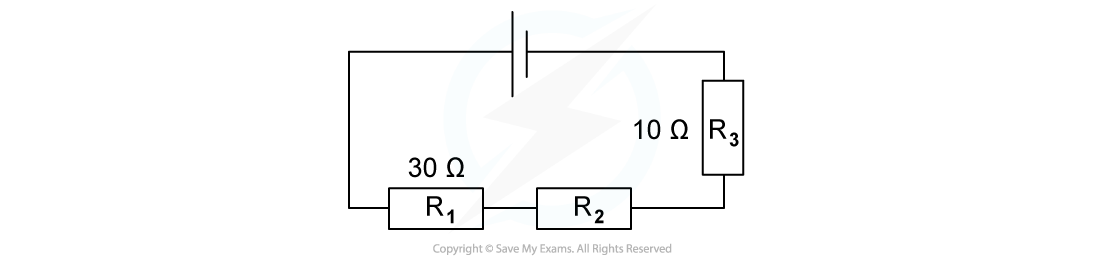
A. 100 Ω
B. 30 Ω
C. 20 Ω
D. 40 Ω
Answer: C
Step 1: Write down the equation for the combined resistance in series
R = R1 + R2 + R3
Step 2: Substitute the values for total resistance R and the other resistors
60 Ω = 30 Ω + R2 + 10 Ω
Step 3: Rearrange for R2
R2 = 60 Ω – 30 Ω – 10 Ω = 20 Ω
Resistors in Parallel
When two or more resistors are connected in parallel, the combined resistance decreases
In the below circuit, the combined resistance of the resistors R1 and R2 is less than if they were connected in series

Resistors connected in parallel
This happens because each resistor creates an extra path along which the charge can flow
This allows more charge to flow overall
This leads to a smaller overall resistance
The advantages of this kind of circuit are:
The components can be individually controlled, using their own switches
If one component stops working the others will continue to function
Examiner Tips and Tricks
Students often struggle to understand how adding resistors to a circuit can actually reduce resistance.
Take a simple series circuit with just a cell, some wires, and a 5 Ω resistor. You now want to add a 10 Ω resistor to that circuit. You have two options; you can add the 10 Ω resistor in series to the 5 Ω resistor or in parallel to it.
If you add the 10 Ω resistor in series, then all of the electrons in the circuit have to flow through both resistors. That's why the resistances add together. The total resistance of the new circuit is 5 + 10 = 15 Ω.
If you add the 10 Ω resistor in parallel, then you are creating a new loop, which is a new path for the electrons to flow through. They either flow through the 5 Ω resistor or they flow through the 10 Ω resistor. Now, because of the extra loop, that extra path for the electrons, there is actually more charge flowing around the circuit than there was before that 10 Ω resistor was added. That means a higher current, which means an overall smaller resistance than the original 5 Ω circuit.
A fundamental concept to understand about circuits is that when you change anything in the circuit (current, p.d., resistance), then everything (current, p.d., resistance) changes as a result.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
