Combination of Transformations (Edexcel GCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Amber

Reviewed by: Dan Finlay

Combination of Transformations

What do I need to know about combined transformations?

Combined transformations are when more than one transformation is performed, one after the other
In many cases, two transformations can be equivalent to one alternative single transformation
- Finding this single transformation is a common exam question

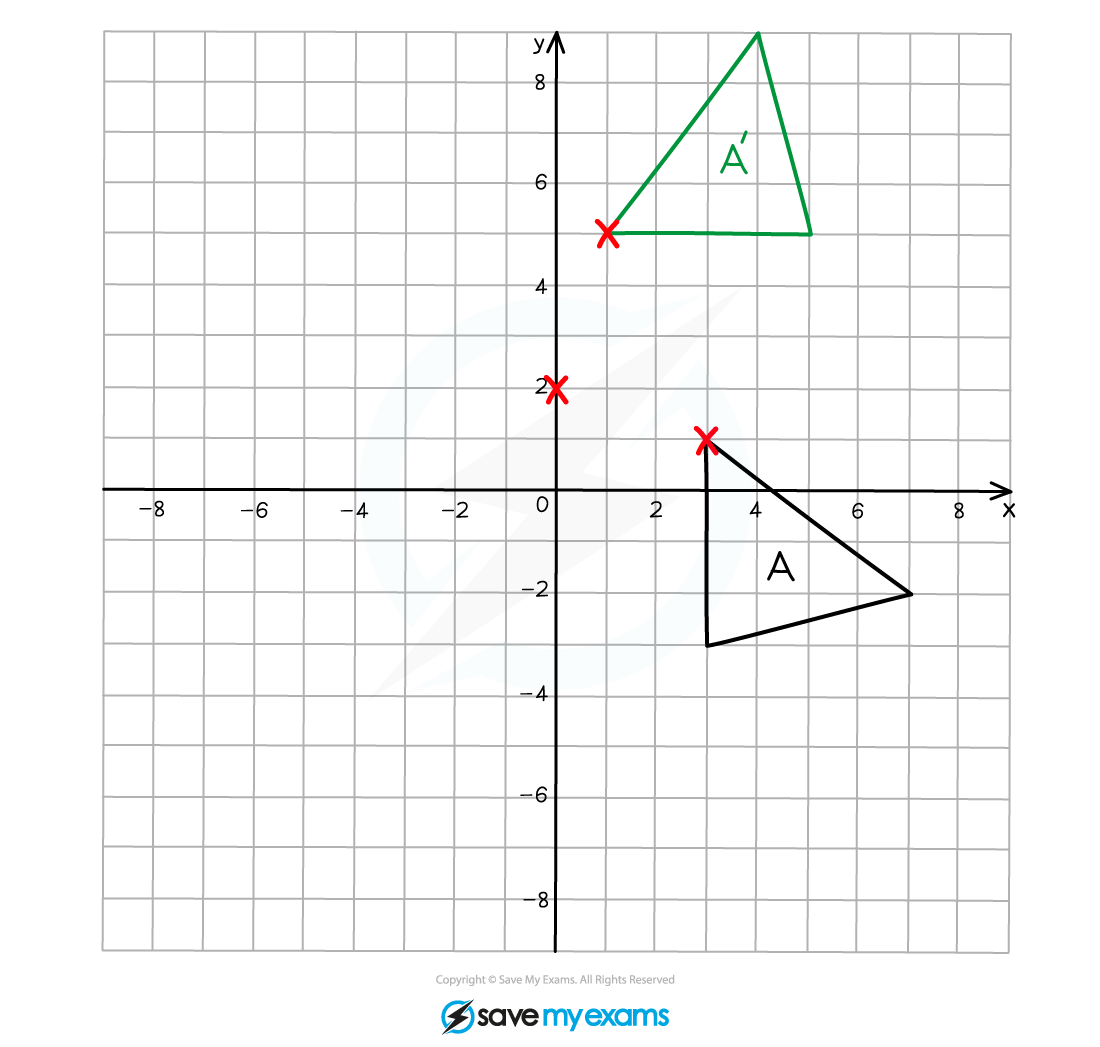
Rotation
- Requires an angle, direction and centre of rotation
- It is usually easy to tell the angle from the orientation of the image
- You can use trial and error and tracing paper to find the centre of enlargement

Shape being rotated 90 degrees anticlockwise about the point (0,2)

Reflection
- A reflection will be in a mirror line which can be vertical (x = k), horizontal (y = k) or diagonal (y = mx + c)
- Points on the mirror line do not move
- It is possible for a mirror line to pass through the object

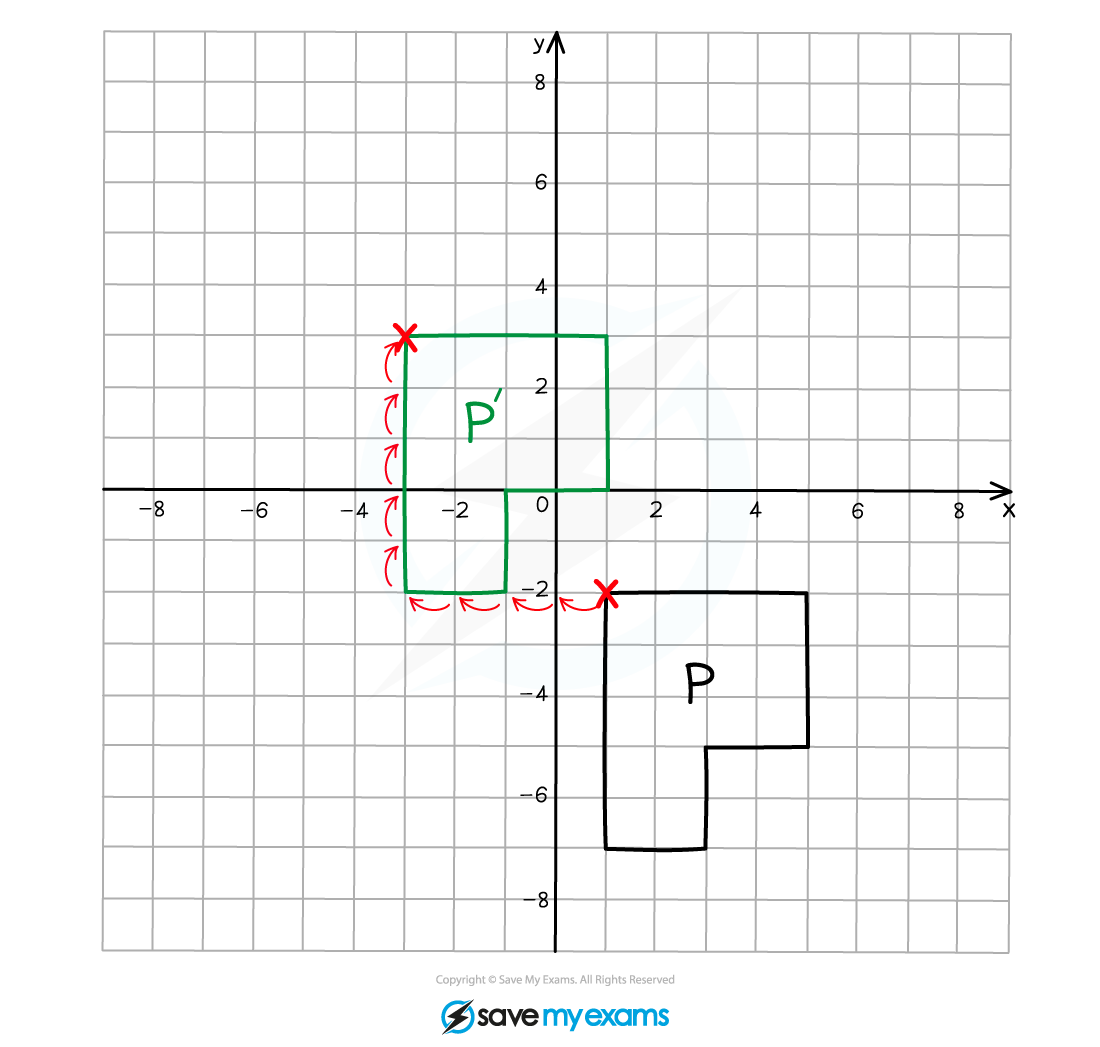
Translation
- A translation is a movement which does not change the orientation or size of the shape, it simply moves location
- A translation is described by a vector in the form $(x y)$
  - This represents a movement of x units to the right and y units vertically upwards

A shape translated 4 units left and 5 units upwards

What are common combinations of transformations?

A combination of two reflections can be the same as a single rotation
- One reflection using the line $x = a$ and the other using the line $y = b$
- This is the same as a 180° rotation about the centre $(a, b)$
The order of the combination can be important to the overall effect
- A reflection in the line y = x followed by a reflection in the x-axis is the same as a 90° rotation clockwise about the origin
- A reflection in the x-axis followed by a reflection in the line y = x is the same as a 90° rotation anticlockwise about the origin

How do I undo a transformation to get back to the original shape?

After transforming shape A to make shape B you could be asked to describe the transformation that maps B to A

Transformation from A to B	Transformation from B to A
Translation by vector $(\begin{matrix} x \\ y \end{matrix})$	Translation by vector $(\begin{matrix} - x \\ - y \end{matrix})$
Reflection in a given line	Reflection in the same line
Rotation by θ° in a direction about the centre $(x, y)$	Rotation by θ° in the opposite direction about the centre $(x, y)$
Enlargement of scale factor $k$ about the centre $(x, y)$	Enlargement of scale factor $\frac{1}{k}$ about the centre $(x, y)$

Worked Example

(a) On the grid below rotate shape F by 180^o using the origin as the centre of rotation.

Label this shape F'.

Combined Q1, IGCSE & GCSE Maths revision notes

Using tracing paper, draw over the original object then place your pencil on the origin and rotate the tracing paper by 180^o
Mark the position of the rotated image onto the coordinate grid

Label the rotated image F'

Combined Q1 Rotation Final, IGCSE & GCSE Maths revision notes

(b) Reflect shape F' in the line $y = 0$ . Label this shape F''.

The line $y = 0$ is the $x$ -axis

Measure the perpendicular distance (the vertical distance) between each vertex on the original object and the $x$ -axis, then measure the same distance on the other side of the mirror line and mark on the corresponding vertex on the reflected image

Repeat this for all of the vertices and join them together to create the reflected image

Label the reflected image F''