3D Shapes (Edexcel GCSE Maths) : Revision Note
Properties of 3D Shapes
What common 3D shapes do I need to know about?
There are a number of common 3D shapes
You should know their names
and their key properties
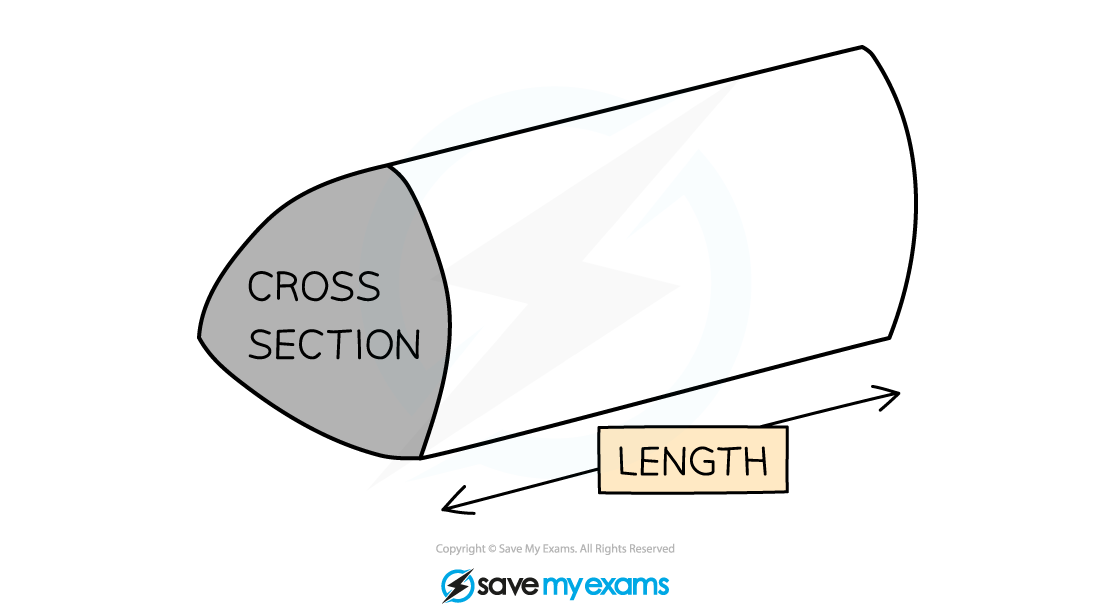
A prism is a 3D shape with the same cross-section throughout
The cross-section of a cube is a square
The cross-section of a cuboid is a rectangle
There are other prisms, such as triangular prisms or hexagonal prisms
In these cases the exam question will make sure the shape of the cross-section is clear
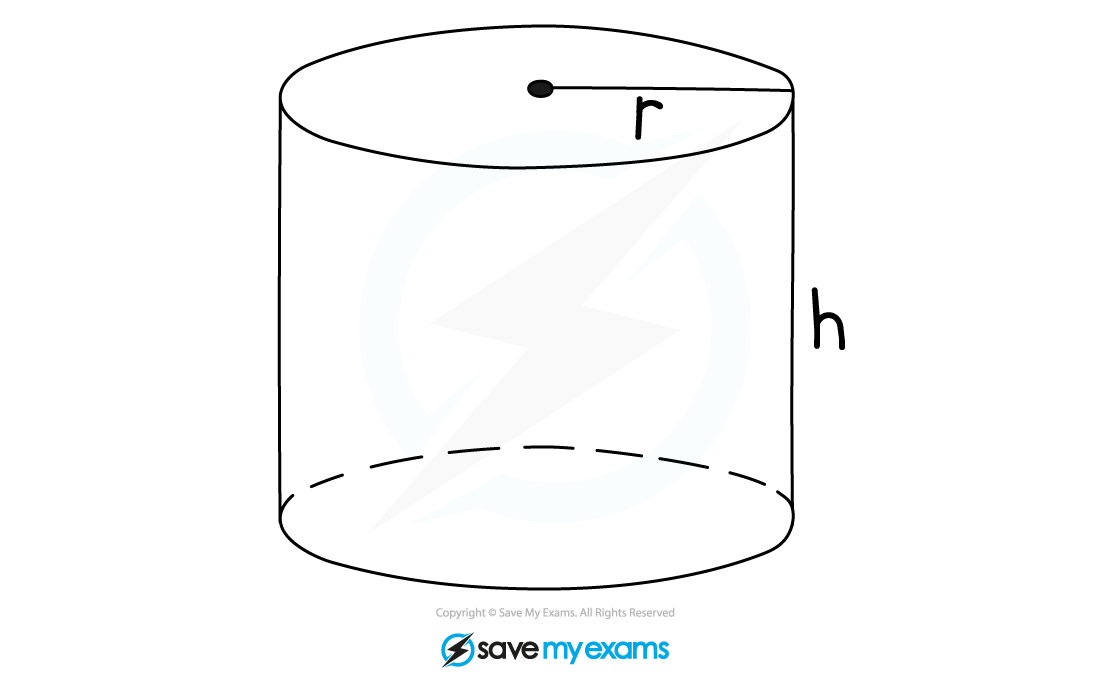
A cylinder is similar to a prism
The cross-section of a cylinder is a circle
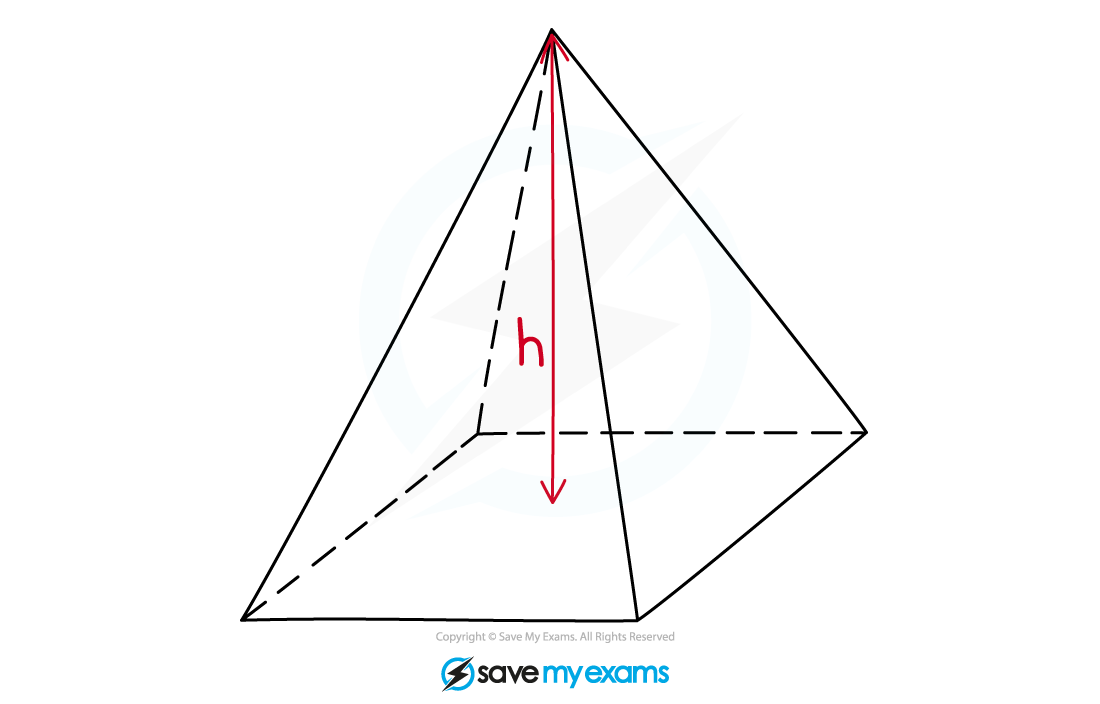
There are a number of different types of pyramid
A pyramid has a flat base and sloping sides that meet at a point
The pyramid may have a square, rectangular or triangular base
Some pyramids have special names you should know
A triangular-based pyramid is called a tetrahedron
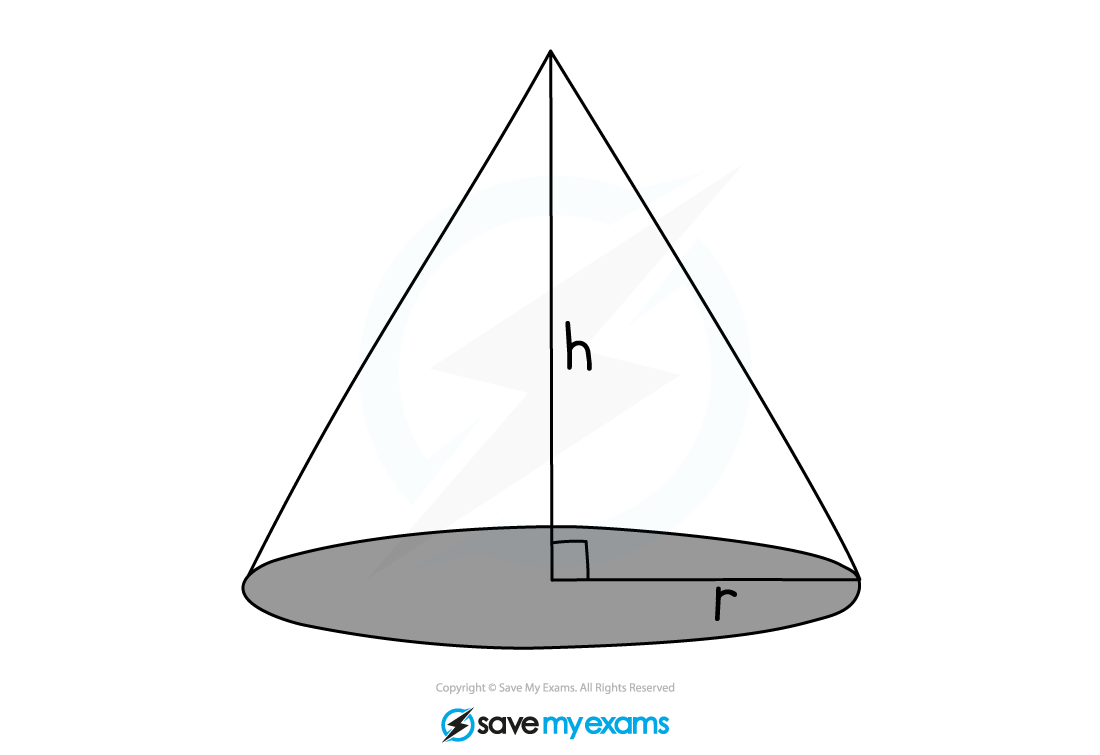
A cone is similar to a pyramid
A cone has a circular base
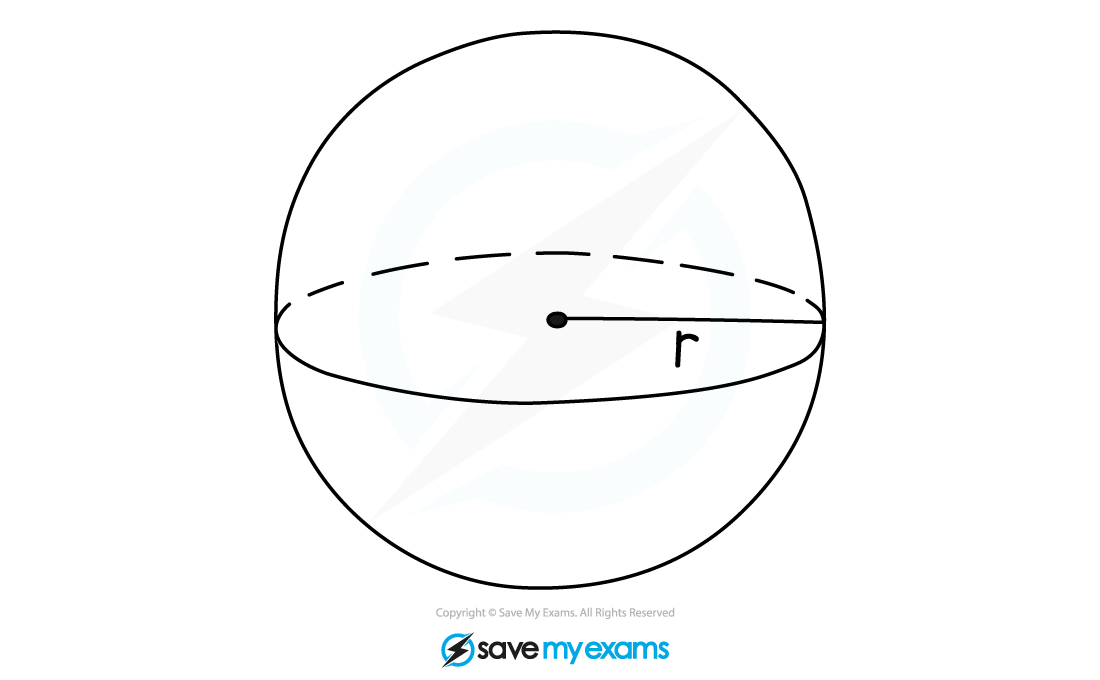
A sphere is a round solid ball shape
What are the properties of 3D shapes?
3D shapes have a number of faces, vertices and edges
A face is a single flat surface of the 3D shape
A vertex (plural, vertices) is a corner of the 3D shape
An edge joins one vertex to another
You should know the number and shape of the faces (and other surfaces) for the common 3D shapes
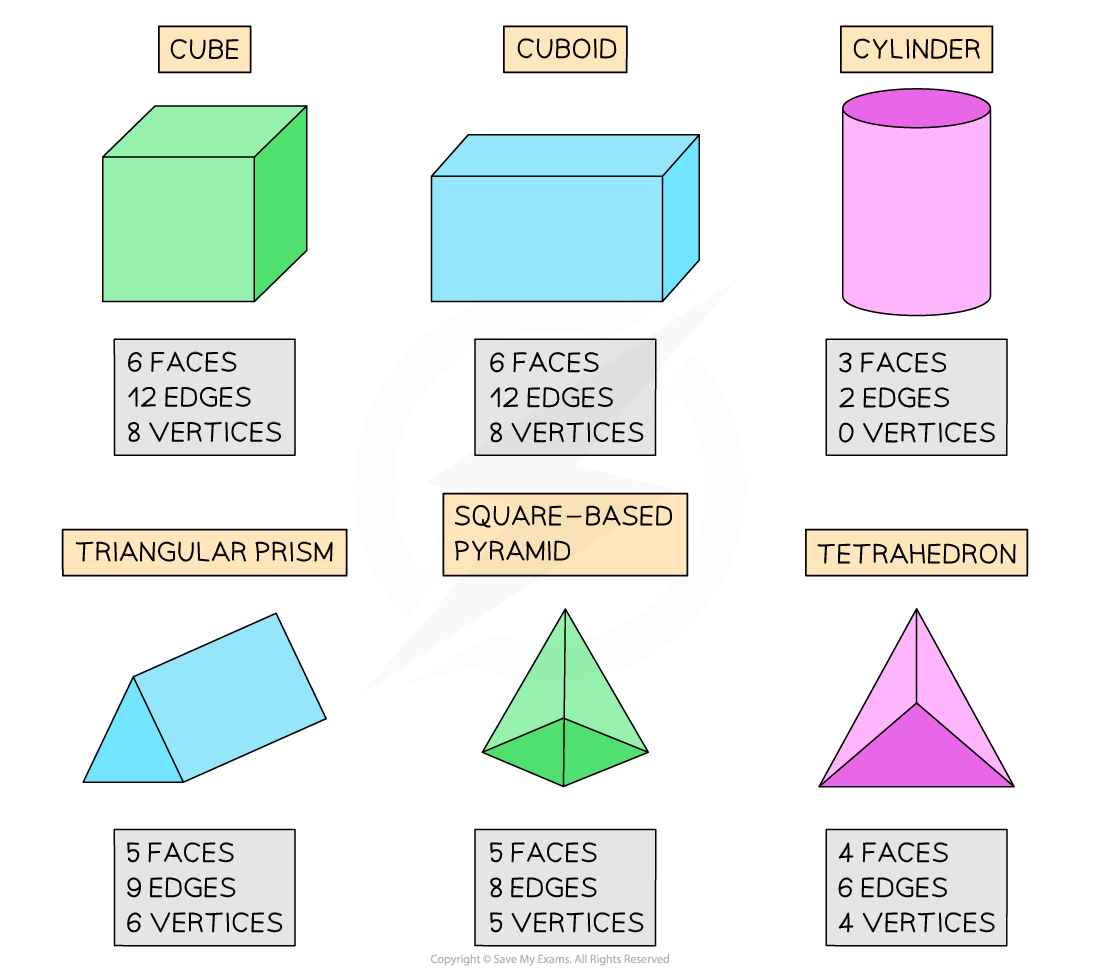
A cube has 6 equal, square faces
A cuboid has 3 pairs of rectangular faces
A cylinder has 2 equal circular faces and 1 curved surface
The curved surface has the shape of a rectangle if laid out flat
A triangular prism has 2 equal triangular faces and 3 rectangular faces
If the triangular faces are equilateral then all of the rectangles will be equal
If the triangular faces are isosceles then two of the rectangles will be equal
A square-based pyramid has 1 square face and 4 equal triangular faces
A tetrahedron has 4 triangular faces
A sphere has 1 curved surface; it is a ball shape
Examiner Tips and Tricks
Remembering the properties of 3D shapes will help in particular with questions involving surface area
What is a net of a solid?
A net of a solid is a 2D drawing that can be cut out and folded to make a 3D shape
Each of the faces of the 3D shape are arranged in a certain pattern
Not every arrangement of the faces will create a net of that solid
Solids can have more than one arrangement that will work to make the 3D shape
The area of the net of a 3D shape is the same as the surface area of the solid
What does the net of a cube or cuboid look like?
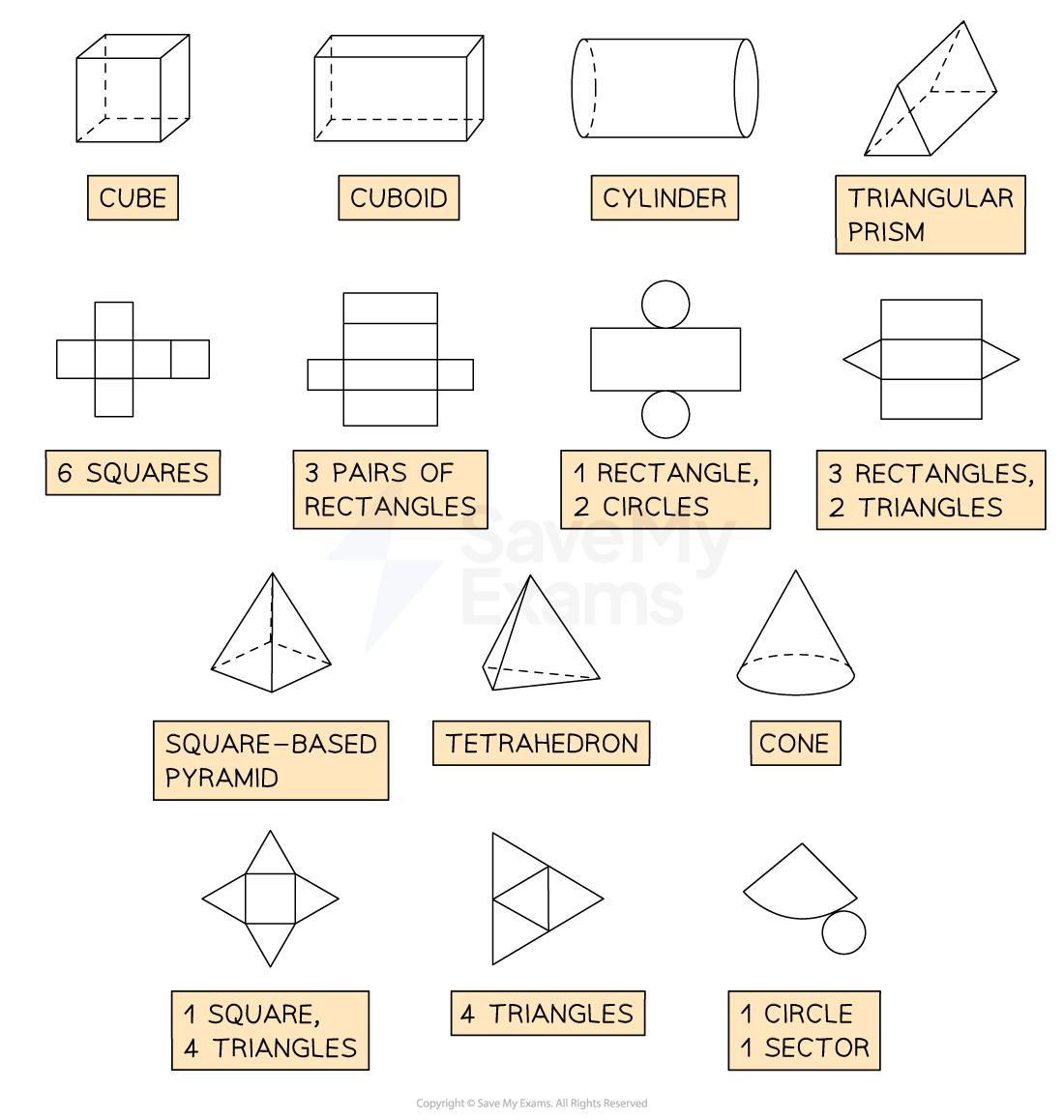
The net of a cube has 6 squares connected at certain edges
There are 11 different arrangements of the square faces that will form a net of a cube

The most common and easiest to remember is in the form of a cross

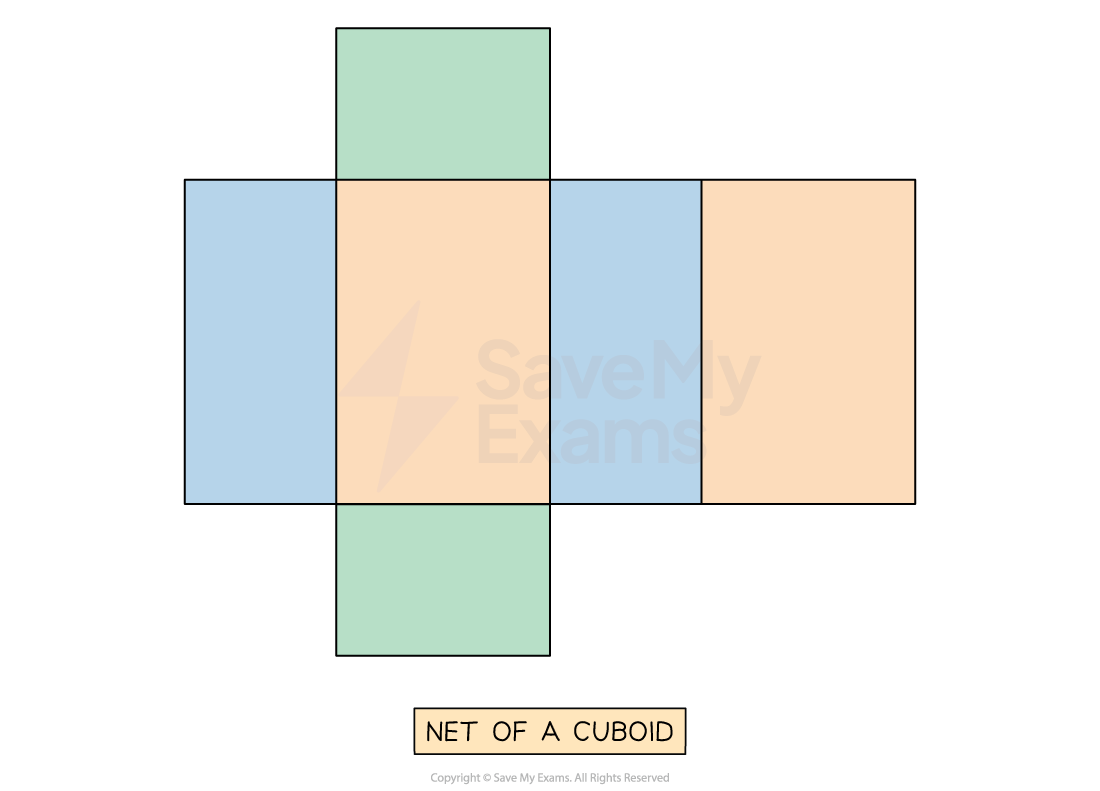
A cuboid has 6 rectangular faces, so its net consists of 6 rectangles
The most common and easiest net to remember is in the form of a cross
Pay attention to which rectangles are the same
They are colour-coded in the diagram below
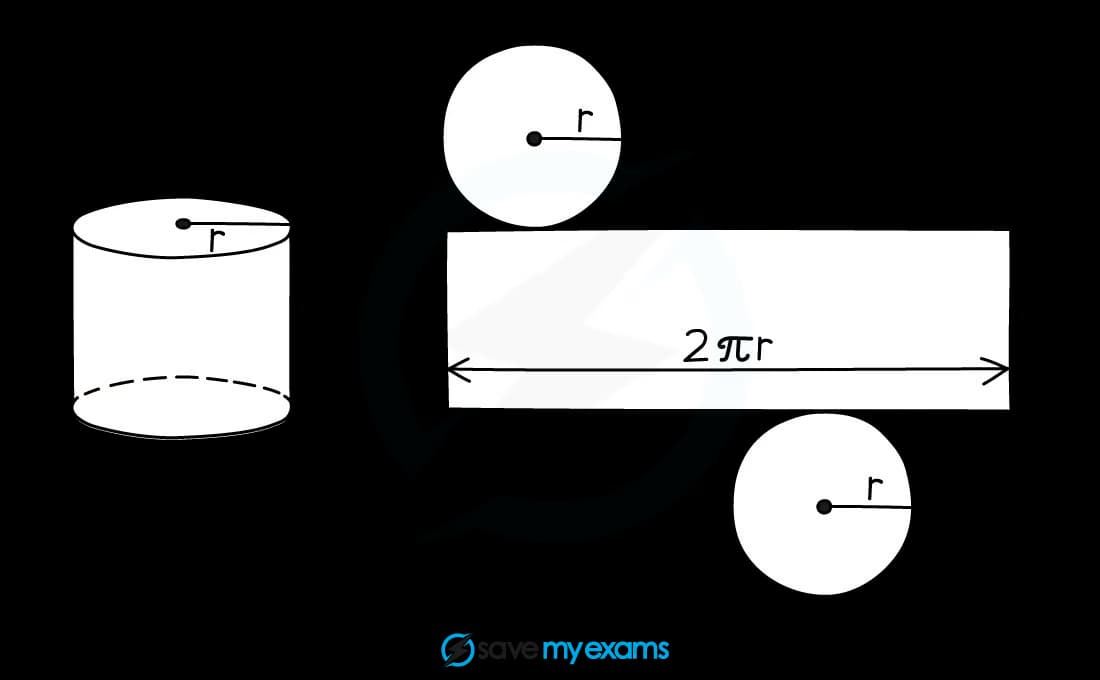
What does the net of a cylinder look like?
The net of a cylinder consists of two circles and a rectangle
The length of the rectangle is equal to the circumference of the circles
The width of the rectangle is equal to the height of the cylinder
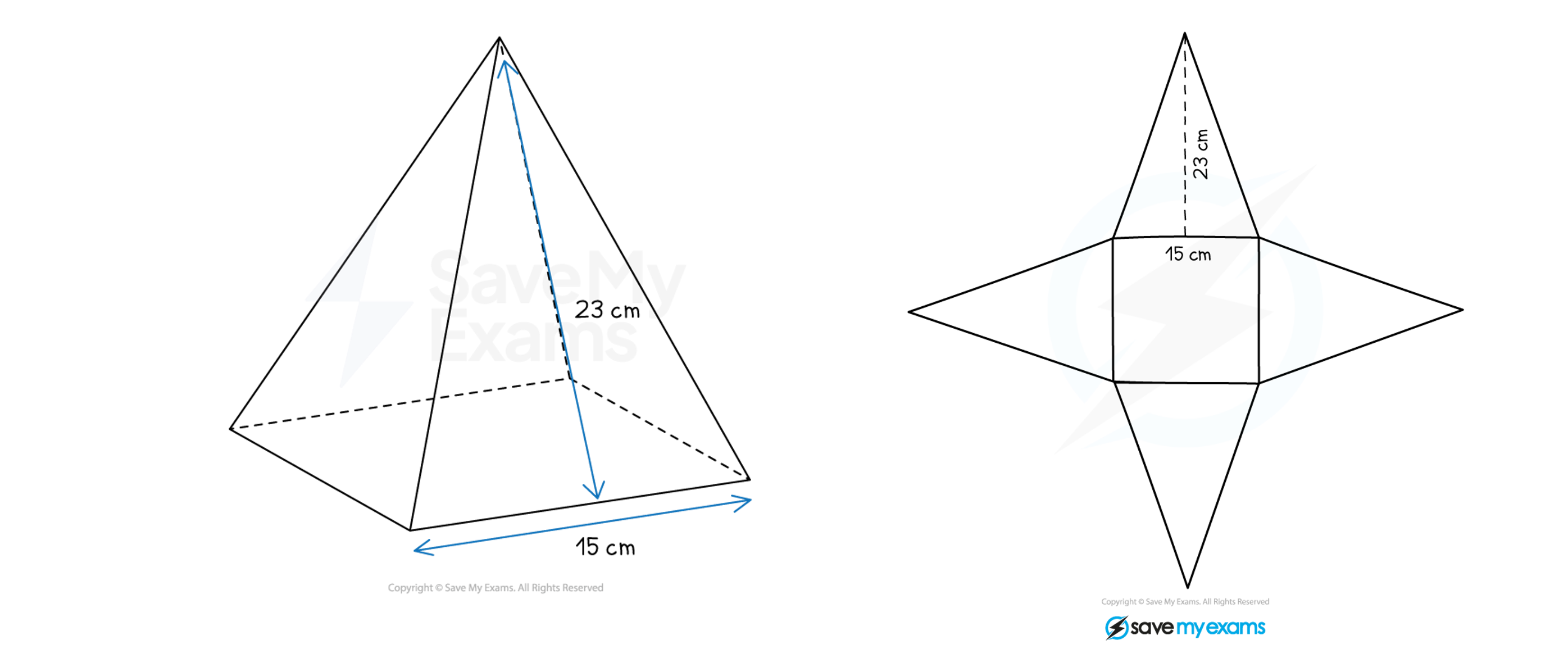
What does the net of a pyramid look like?
The net of a pyramid consists of the base and a triangle attached to each edge of the base
For example, a square-based pyramid has a square base and four congruent (identical) triangles
The perpendicular height of each triangle is equal to the slant height of the pyramid
Examiner Tips and Tricks
You may be given the dimensions of the solid when asked to draw a net
Make sure you put the correct lengths in the correct places by imagining cutting out and folding up the net
Worked Example
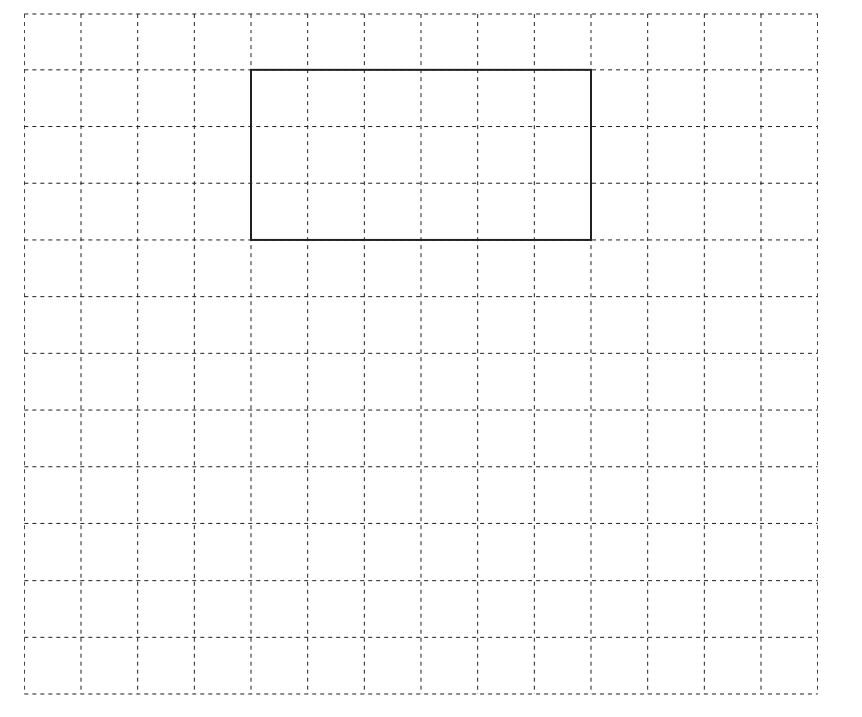
A cuboid measures 6 cm by 3 cm by 2 cm.
On the 1 cm2 grid, draw an accurate net of this cuboid. One face has been drawn for you.
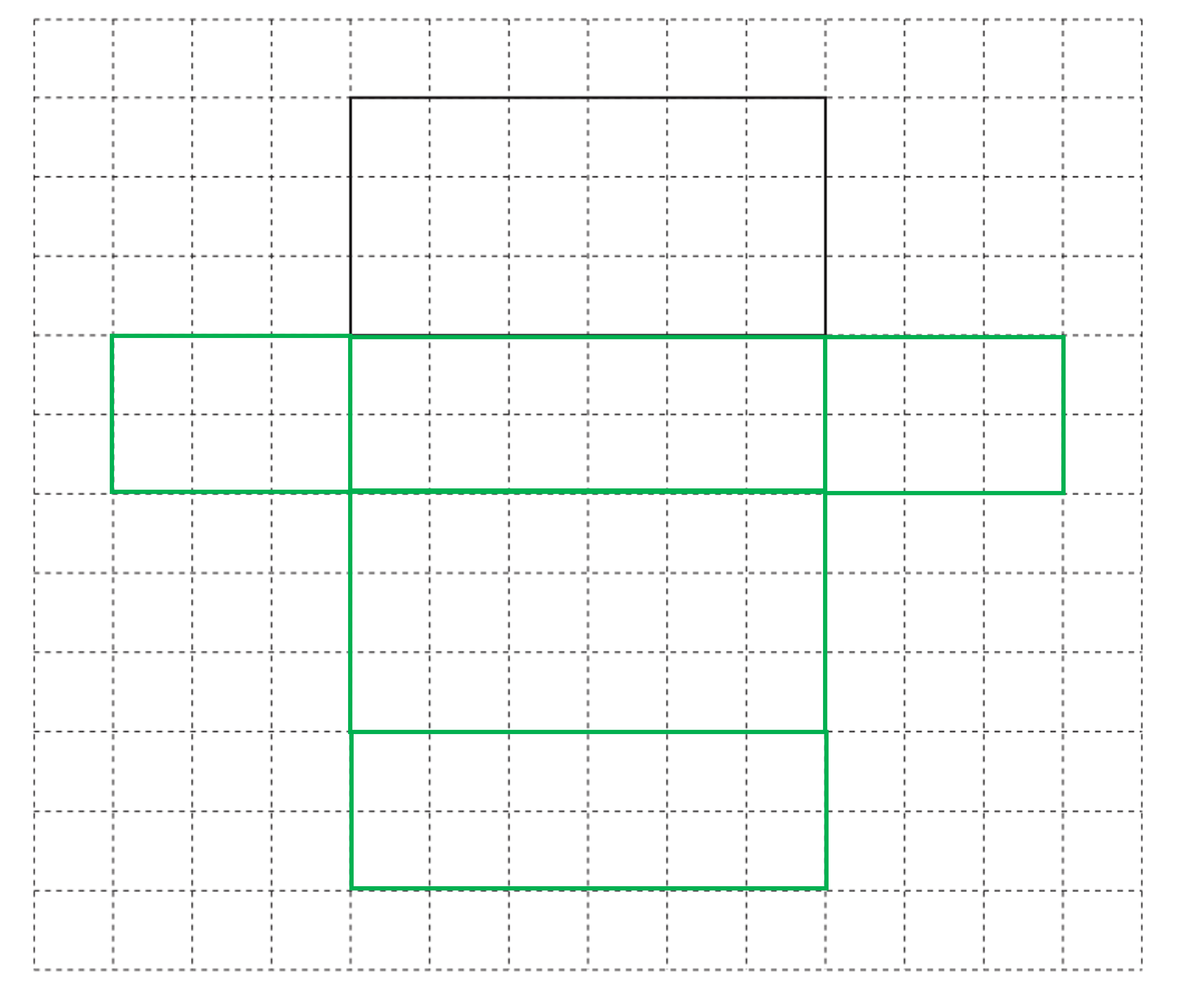
The cuboid has three pairs of rectangles; measuring 6 cm by 3 cm, 6 cm by 2 cm, and 3 cm by 2 cm
Make sure the net has two of each of these rectangles in the correct places

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

