Translations of Graphs (Edexcel GCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Naomi C

Reviewed by: Dan Finlay

Did this video help you?

Translations of Graphs

What are translations of graphs?

The equation of a graph can be changed in certain ways
- This has an effect on the graph
  - How a graph changes is called a graph transformation
A translation is a type of graph transformation that shifts (moves) a graph (up or down, left or right) in the xy plane
- The shape, size, and orientation of the graph remain unchanged

A particular translation is specified by a translation vector

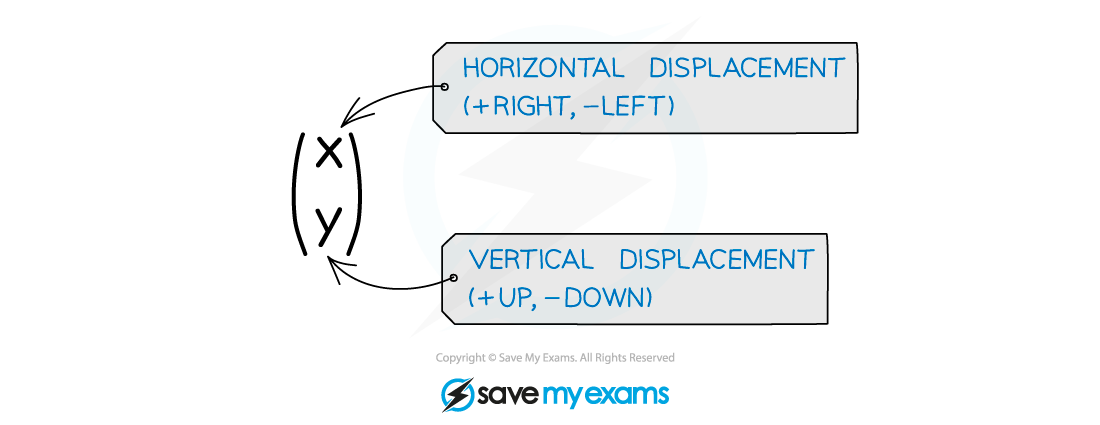
How do I translate graphs?

Let $y = f (x)$ be the equation of the original graph

Vertical translations: y=f(x) + a

$y = f (x) + a$ is a vertical translation by the vector $(\begin{matrix} 0 \\ a \end{matrix})$
- The graph moves up for positive values of $a$
- The graph moves down for negative values of $a$
- The x-coordinates stay the same

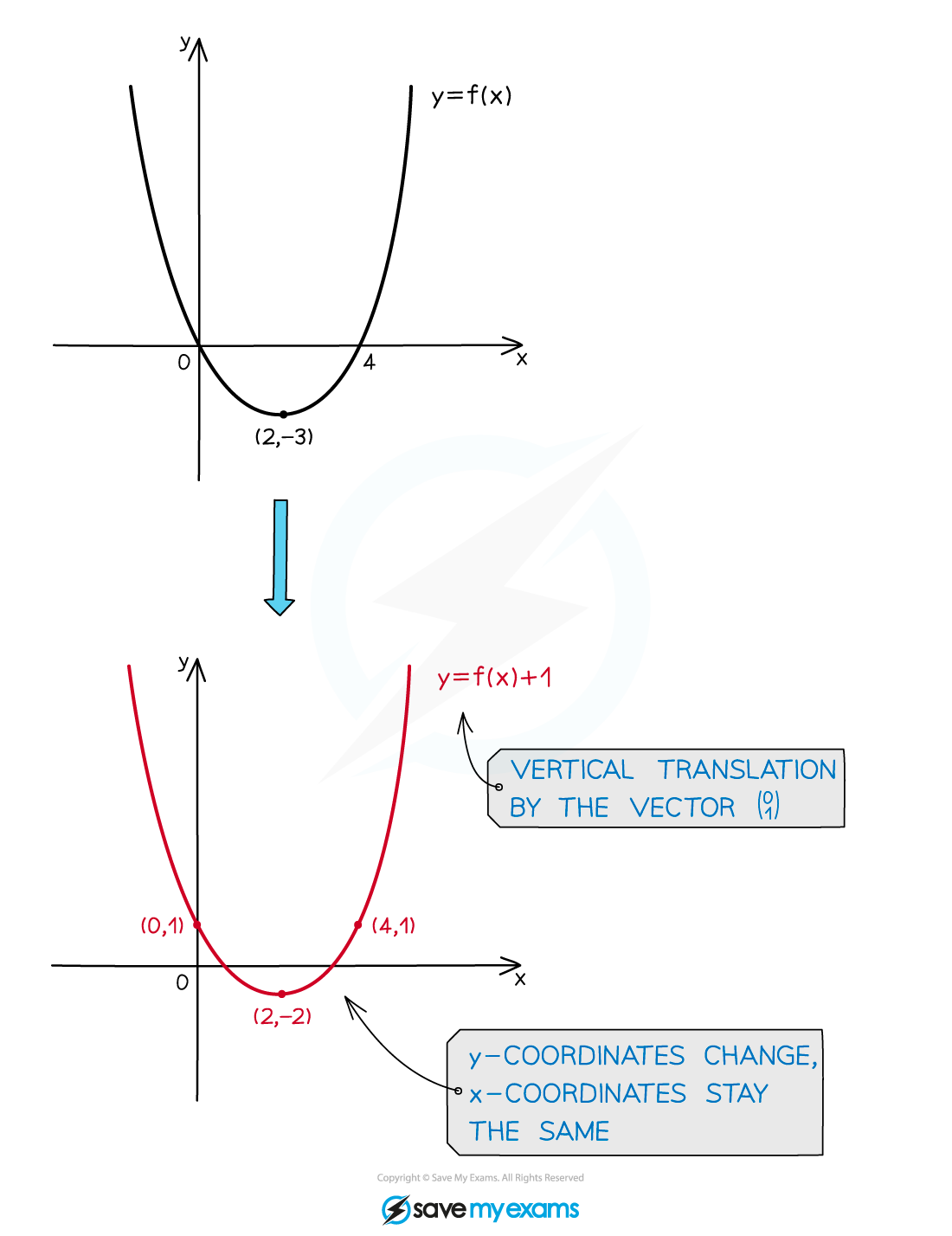
Vertical translation of a graph by the vector (0, 1)

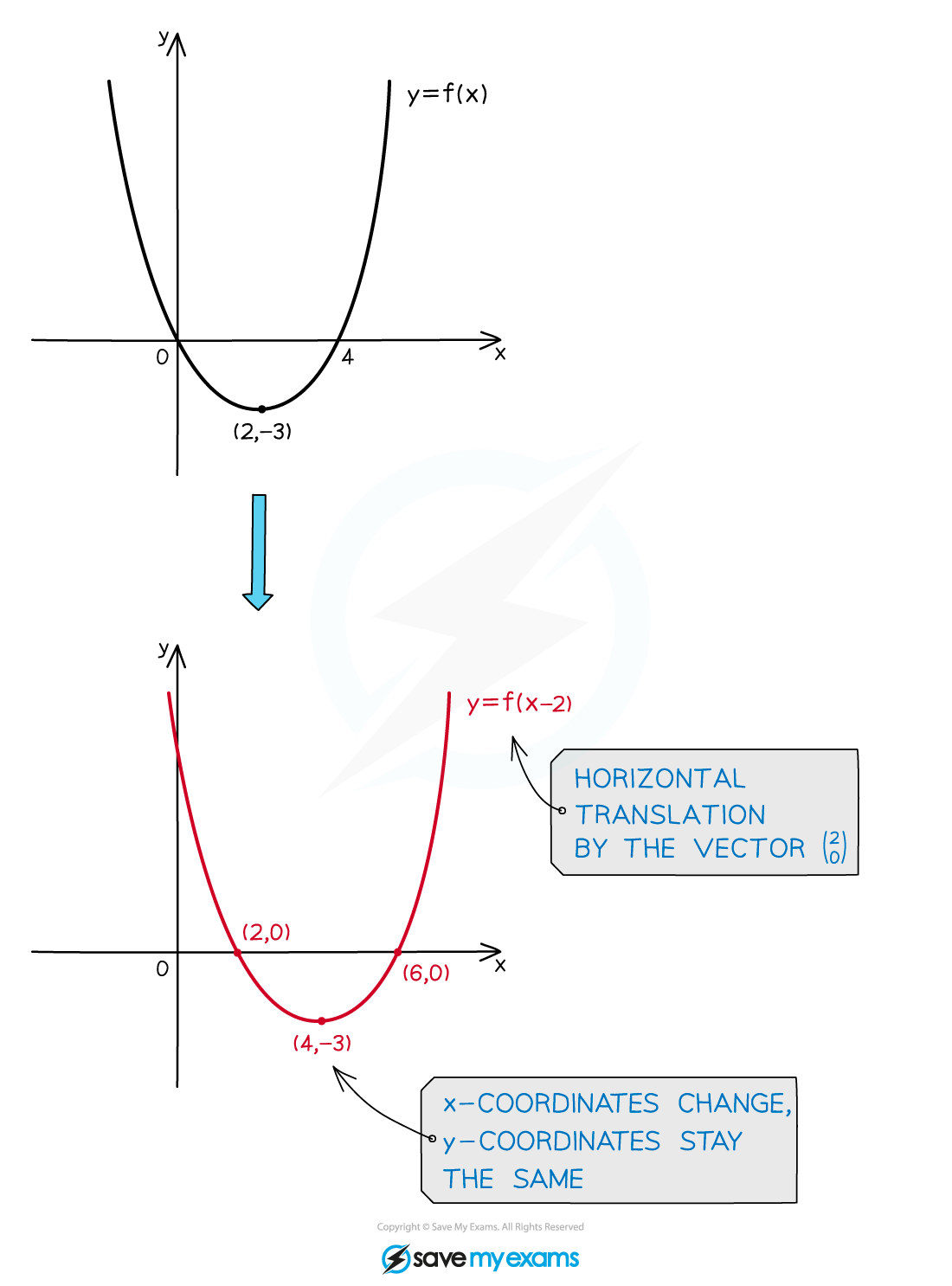
Horizontal translations: y=f(x + a)

$y = f (x + a)$ is a horizontal translation by the vector $(\begin{matrix} - a \\ 0 \end{matrix})$
- The graph moves left for positive values of $a$
  - This is often the opposite direction to which people expect
- The graph moves right for negative values of $a$
- The y-coordinates stay the same

Horizontal translation of a graph by the vector (2, 0)

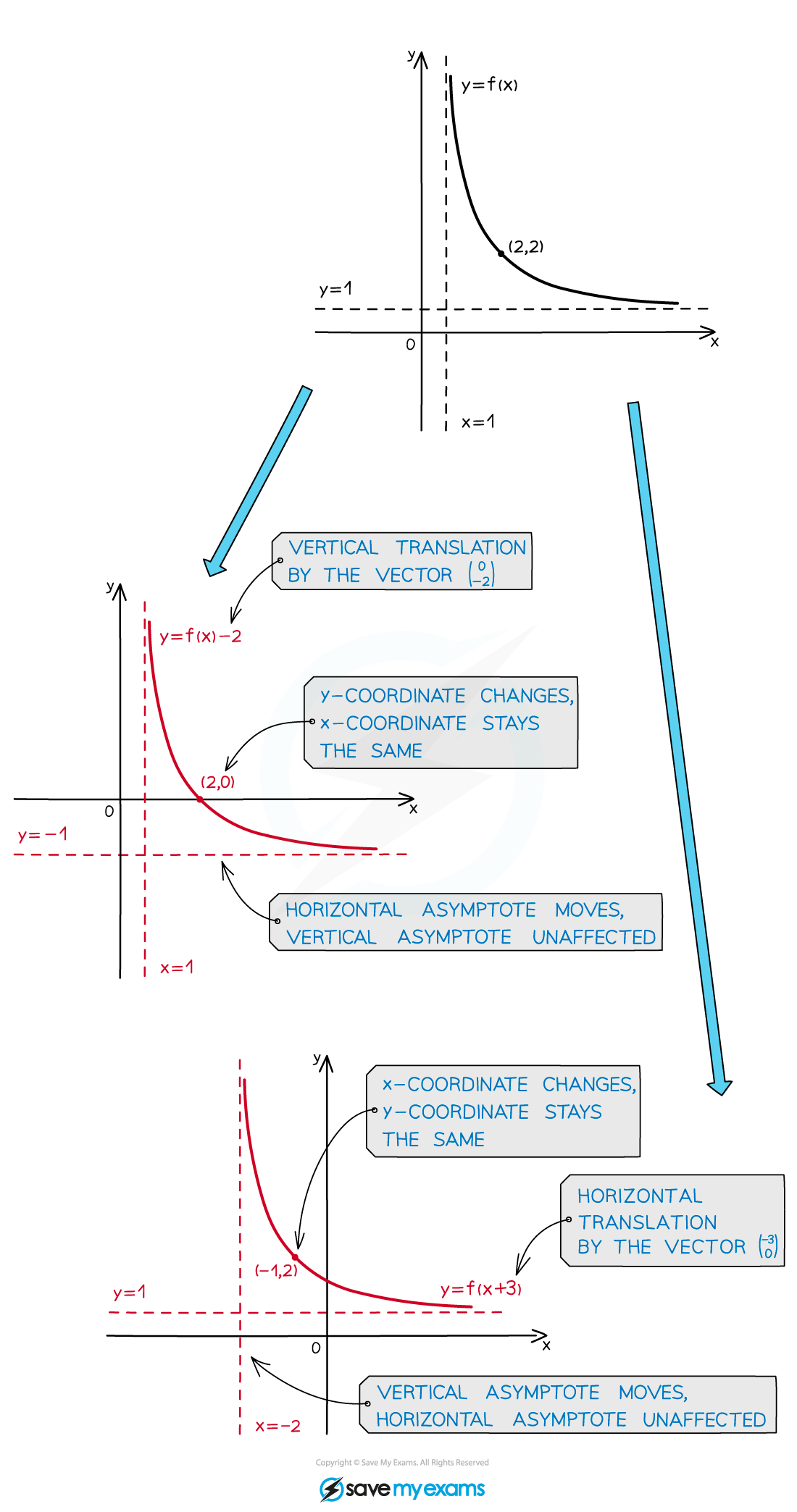
What happens to asymptotes when a graph is translated?

Any asymptotes of f(x) are also translated
- An asymptote parallel to the direction of translation will not be affected

How does a translation affect the equation of the graph?

For a horizontal translation $y = f (x - a)$ of the graph $y = f (x)$
- $a$ is subtracted from $x$ throughout the equation
- Every instance of $x$ in the equation is replaced with $(x - a)$
E.g. the graph $y = x^{2} - 3 x + 7$ undergoes a translation of 6 units to the right
- $y = f (x)$ becomes $y = f (x - 6)$
- $x$ is replaced throughout the equation by $(x - 6)$
  - $y = {(x - 6)}^{2} - 3 (x - 6) + 7$ is the new equation
- The equation can be left in this form or expanded and simplified
  - $y = x^{2} - 12 x + 36 - 3 x + 18 + 7$
  - $y = x^{2} - 15 x + 61$
For a vertical translation $y = f (x) + a$ of the graph $y = f (x)$
- $a$ is added to the equation as a whole
E.g. the graph $y = 4 x^{2} + 2 x + 1$ undergoes a translation of 5 units down
- $y = f (x)$ becomes $y = f (x) - 5$
- 5 is subtracted from the equation as a whole
  - $y = 4 x^{2} + 2 x + 1 - 5$
- The equation can be left in this form or simplified
  - $y = 4 x^{2} + 2 x - 4$

How do I apply a combined translation?

For a horizontal translation of $p$ units and vertical translation of $q$ units combined
- $y = f (x)$ becomes $y = f (x - p) + q$
E.g. the graph $y = 3 x^{2}$ undergoes a translation of 2 units up and 1 unit to the left
- $y = f (x)$ will become $y = f (x + 1) + 2$
- $x$ is replaced throughout the equation by $(x + 1)$
- 2 is added to the equation as a whole
  - $y = 3 {(x + 1)}^{2} + 2$

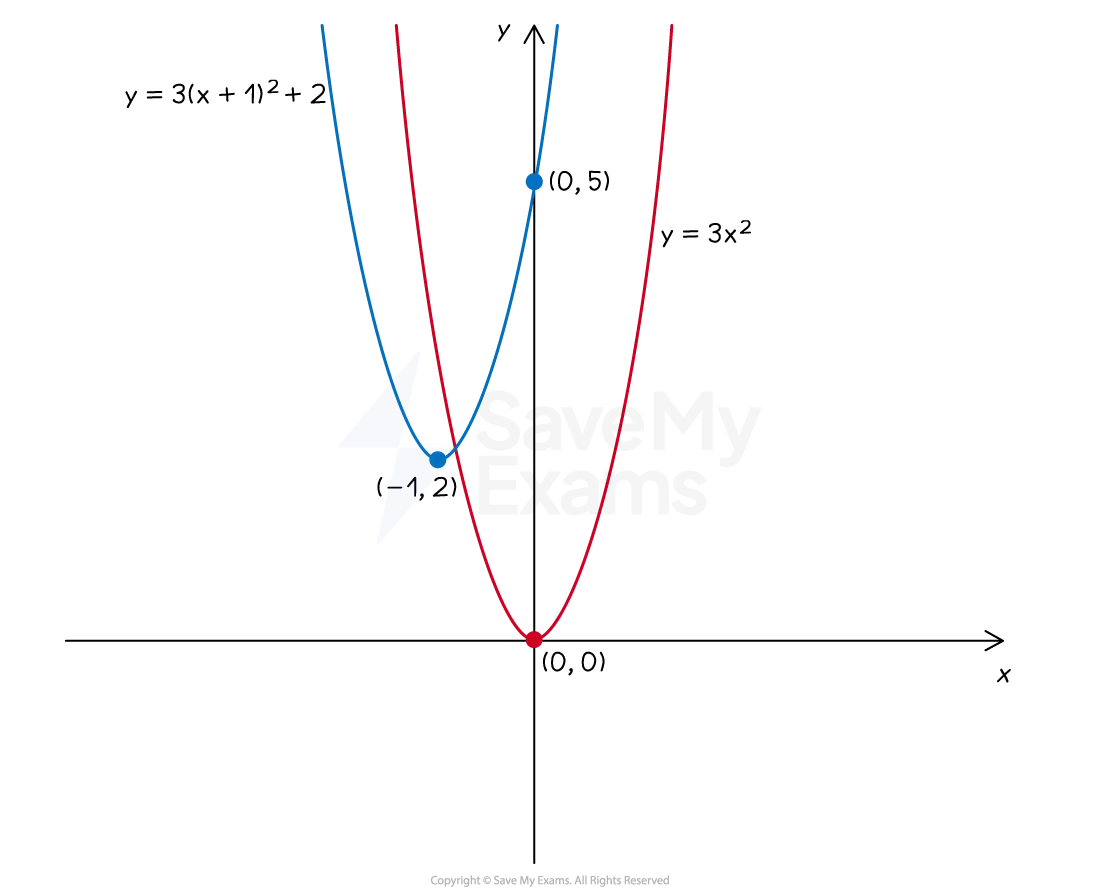
Transformation of the graph y=3x^2 by a horizontal translation of -1 and vertical translation of +2.

Note that when the equation is in the form $y = a {(x - p)}^{2} + q$
- the vertex is $(p, q)$
- the value of $a$ does not affect the vertex coordinates

Worked Example

The diagram below shows the graph of $y = f (x)$ .

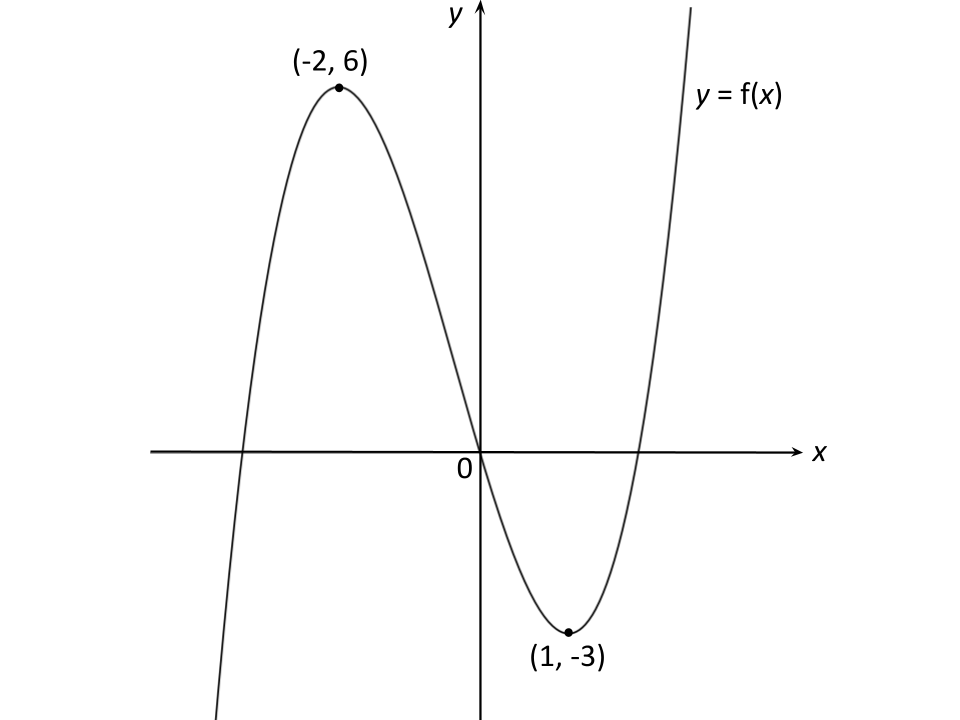
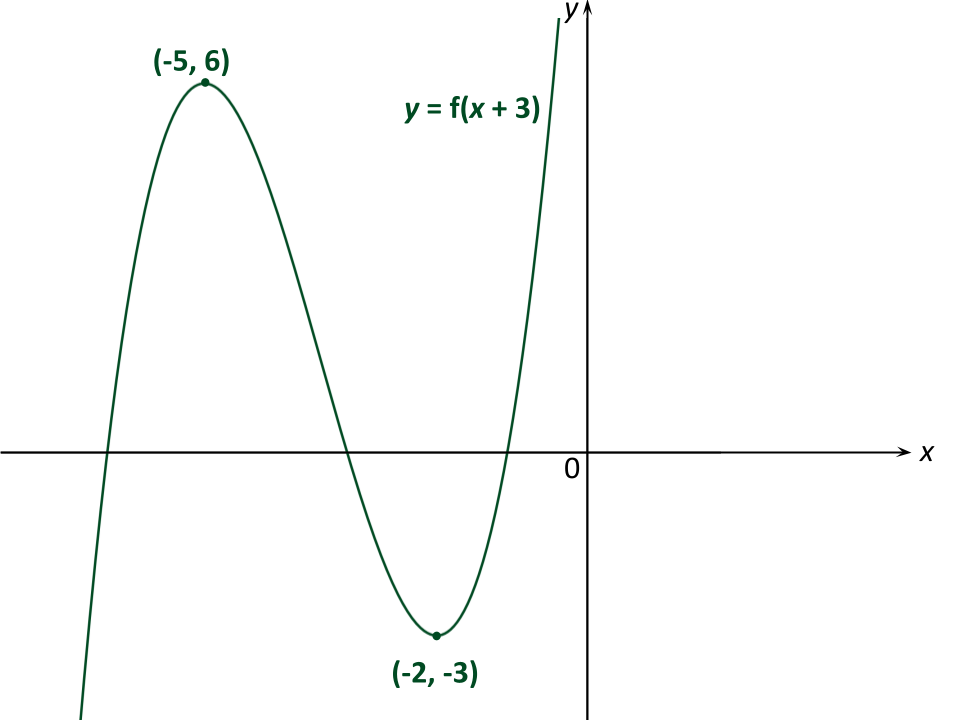
Sketch the graph of $y = f (x + 3)$ .

The transformation of the graph is a horizontal translation with vector $(\begin{matrix} - 3 \\ 0 \end{matrix})$ (3 units to the left)

The x-coordinates of the points change (subtract 3 from each)
The y-coordinates of the points stay the same

Last updated: 18 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: