Reflections of Graphs (Edexcel GCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Mark Curtis

Reviewed by: Dan Finlay

Did this video help you?

Reflections of Graphs

What are reflections of graphs?

Reflections of graphs are a type of transformation where the curve is reflected about one of the axes

Two graphs showing curves and their reflections. The curve is reflected in the x-axis (left) and y-axis (right). — **A curve reflected in the x-axis (left) and y-axis (right)**

How do I reflect graphs?

Let $y = f (x)$ be the equation of the original graph

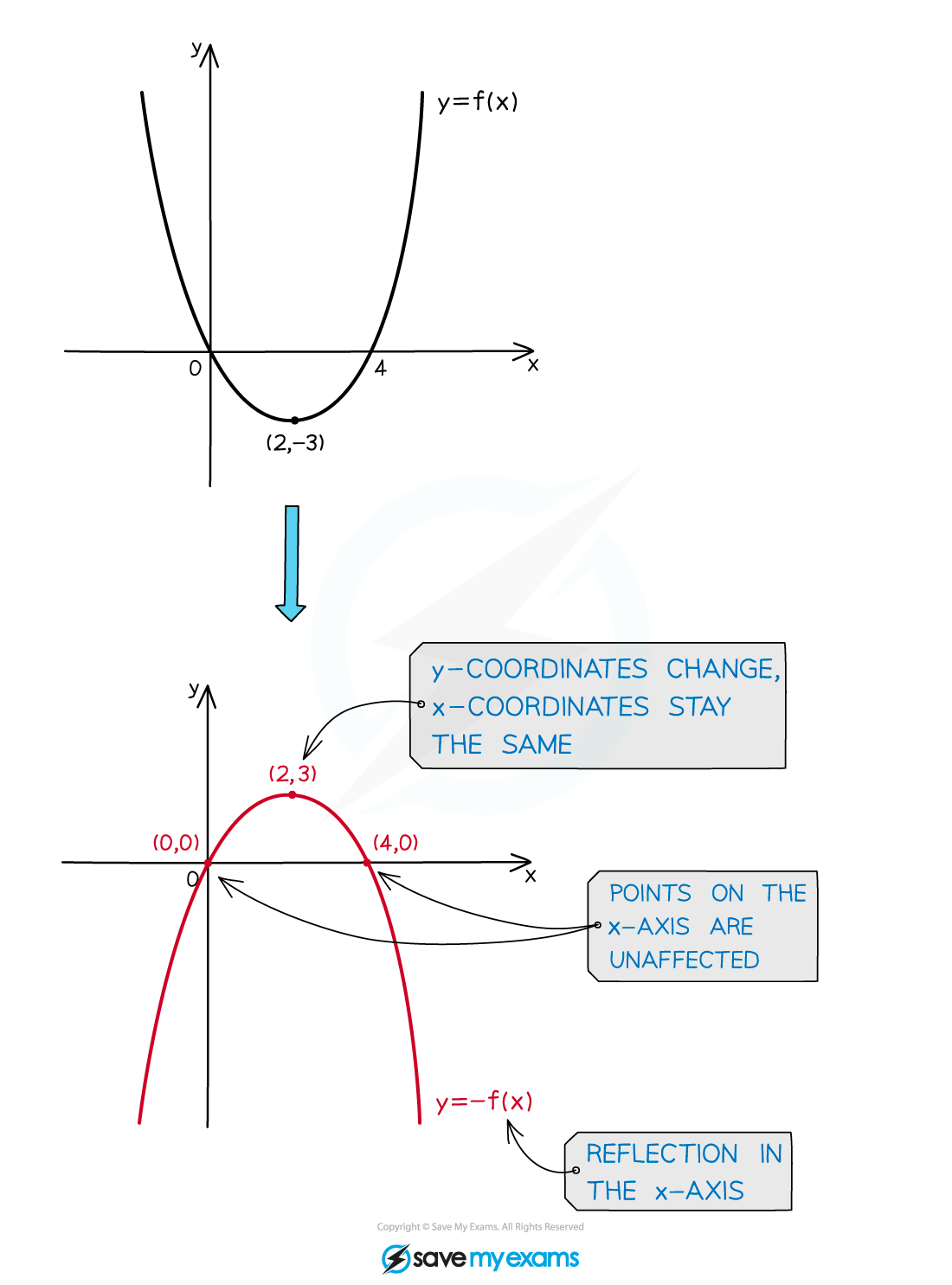
Vertical reflections: y=-f(x)

$y = - f (x)$ is a reflection in the $x$ -axis
- The $y$ coordinates change sign
  - The $x$ coordinates are unaffected

Graph showing the reflection of a parabola y=f(x) in the x-axis to y=-f(x). Key points are (2,-3) reflecting to (2,3), demonstrating y-coordinate change only.

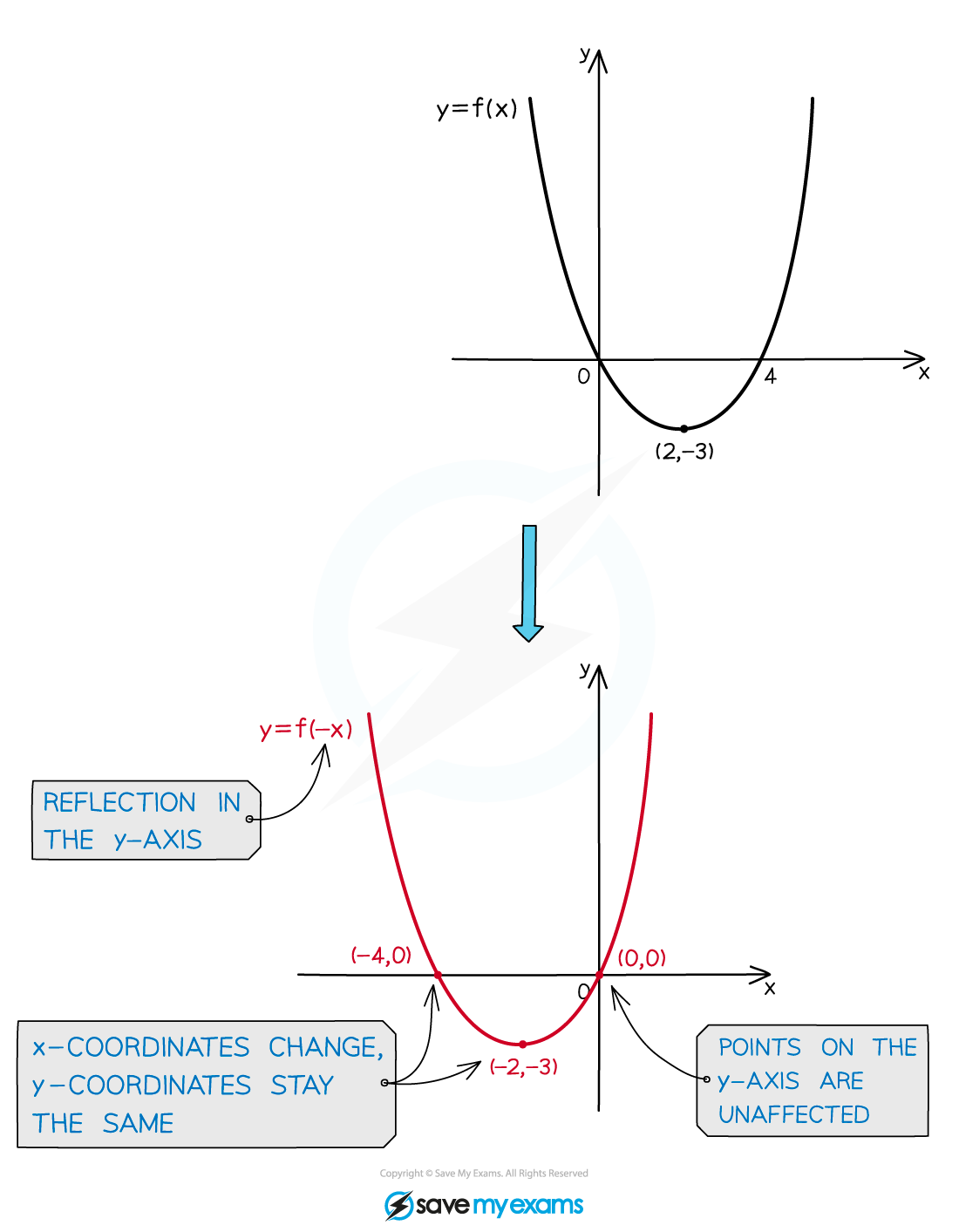
Horizontal reflections: y=f-(x)

$y = f (- x)$ is a reflection in the $y$ -axis
- The $x$ coordinates change sign
  - The $y$ coordinates are unaffected

Graph showing function y=f(x) reflected in the y-axis to y=f(-x). Points on graph change x-coordinates but retain y-coordinates; points on y-axis remain affected.

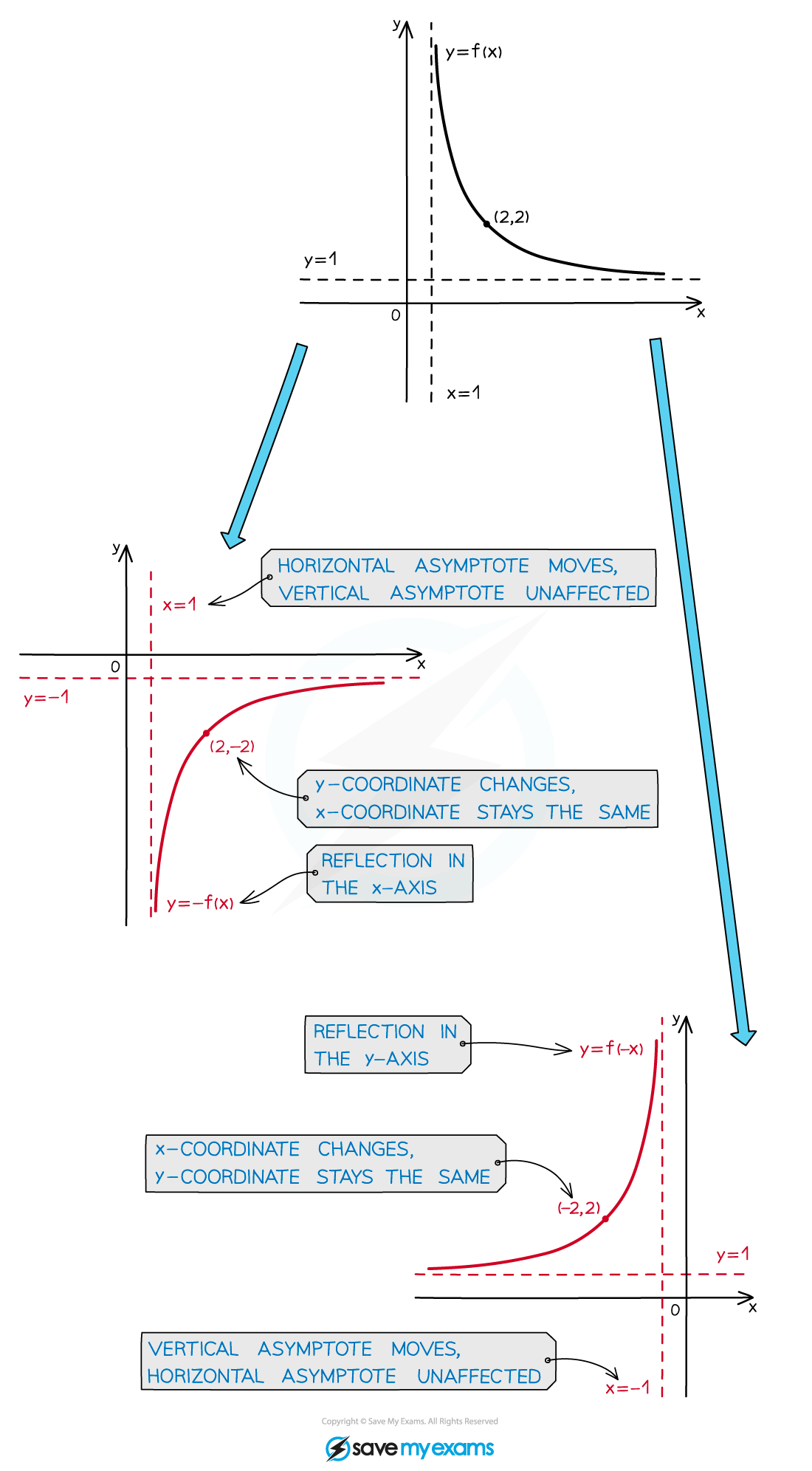
What happens to asymptotes when a graph is reflected?

Any asymptotes of $f (x)$ are also reflected

When a graph is reflected, any asymptotes are reflected too

Examiner Tips and Tricks

When reflecting graphs in the exam, reflect any key points on the graph first, then join them up with a smooth curve.

How does a reflection affect the equation of the graph?

When a graph is reflected, you can change its equation algebraically
- There is no need to sketch the graph
Reflecting in the $x$ -axis puts a $-$ in front of the whole equation
- For example, $y = x^{2} + 2 x$ becomes $y = - (x^{2} + 2 x)$
  - This simplifies to $y = - x^{2} - 2 x$
Reflecting in the $y$ -axis replaces any $x$ with $(- x)$ in the equation
- For example, $y = x^{2} + 2 x$ becomes $y = {(- x)}^{2} + 2 (- x)$
  - This simplifies to $y = x^{2} - 2 x$

How do I apply a combined reflection?

The graph of $y = - f (- x)$ is a combined reflection in both the $x$ and $y$ axes
- It does not matter which order you apply these in
  - For example, reflect about the $y$ -axis then about the $x$ -axis

Worked Example

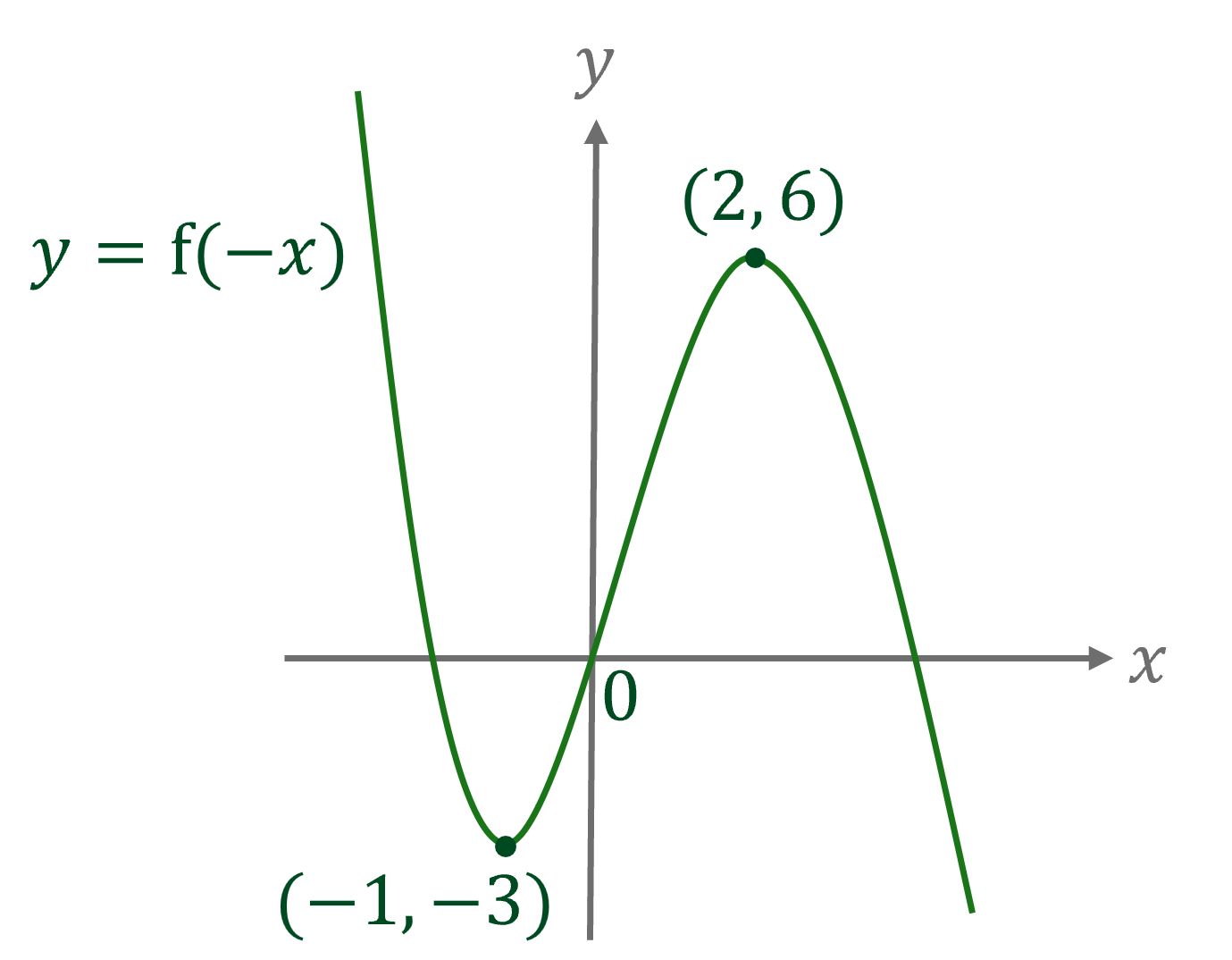
The diagram below shows the graph of $y = f (x)$ .

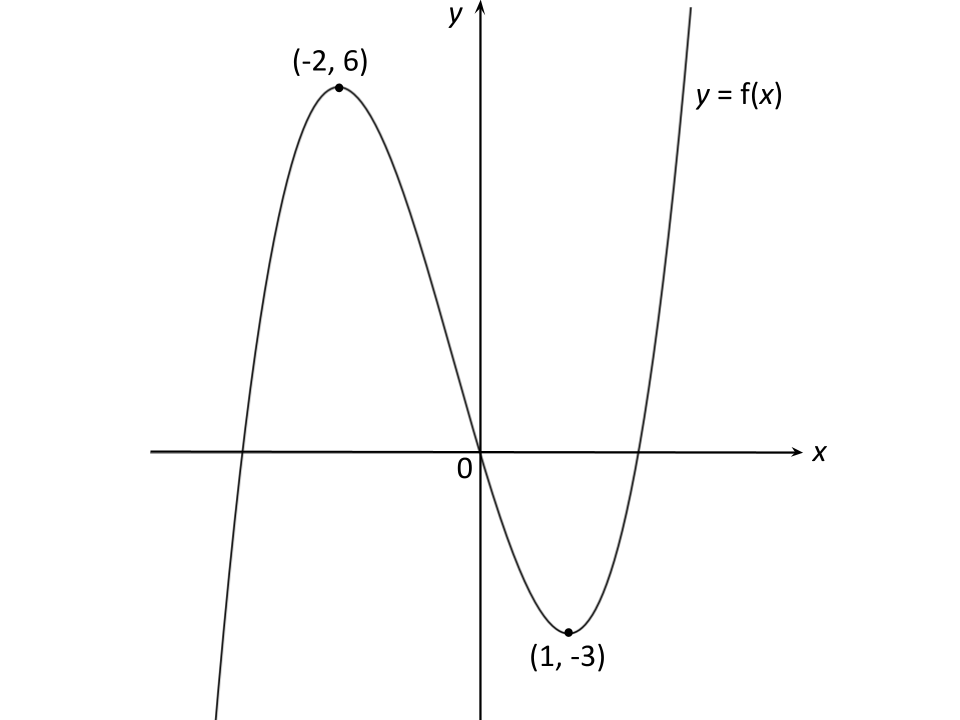
Sketch the graph of $y = f (- x)$ .

The transformation $y = f (- x)$ is a reflection in the $y$ -axis
Reflect the points (-2, 6) and (1, -3) in the $y$ -axis to get (2, 6) and (-1, -3)
Sketch these points and join with a smooth curve through the origin

Graph of y = f(-x) showing a curve with labelled points (-1, -3) at the minimum and (2, 6) at the maximum.

Last updated: 18 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: